甄鵬華,，于振梅
(山東女子學(xué)院 信息技術(shù)學(xué)院,， 山東 濟(jì)南 250300)
摘要：數(shù)字電子計(jì)算機(jī)是一個(gè)離散結(jié)構(gòu)，它只能處理離散的或離散化了的數(shù)量關(guān)系,，因此，無論計(jì)算機(jī)科學(xué)本身,，還是與計(jì)算機(jī)科學(xué)及其應(yīng)用密切相關(guān)的現(xiàn)代科學(xué)研究領(lǐng)域,，都面臨著如何對(duì)離散結(jié)構(gòu)建立相應(yīng)的數(shù)學(xué)模型，以及如何將已用連續(xù)數(shù)量關(guān)系建立起來的數(shù)學(xué)模型離散化,，從而由計(jì)算機(jī)加以處理的問題,。實(shí)際上，可以將離散數(shù)學(xué)理解為對(duì)計(jì)算機(jī)問題的抽象,，離散性可以在算法設(shè)計(jì)和數(shù)據(jù)結(jié)構(gòu)中體現(xiàn),。計(jì)算機(jī)中也有其他的問題表現(xiàn)出了離散性，所以,，計(jì)算機(jī)科學(xué)對(duì)離散數(shù)學(xué)的研究不應(yīng)太過局限,，這些表現(xiàn)都可以歸結(jié)為計(jì)算機(jī)所采用的二進(jìn)制。
關(guān)鍵詞：離散數(shù)學(xué),；算法設(shè)計(jì),；數(shù)據(jù)結(jié)構(gòu)；離散性,；二進(jìn)制
中圖分類號(hào)：TP301文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.16747720.2016.22.005
引用格式：甄鵬華,于振梅. 計(jì)算機(jī)科學(xué)中的算法設(shè)計(jì)與數(shù)據(jù)結(jié)構(gòu)的離散性［J］.微型機(jī)與應(yīng)用,，2016,35（22）：18-21.
0引言
計(jì)算機(jī)科學(xué)(Computer Science)是一門日新月異的學(xué)科。計(jì)算機(jī)科學(xué)與技術(shù)專業(yè)的研究人員時(shí)刻站在國(guó)際先進(jìn)科技的前沿,，學(xué)習(xí)新知識(shí),，并向創(chuàng)造新知識(shí)而努力。
但是計(jì)算機(jī)科學(xué)中亦有許多基礎(chǔ)科學(xué)中的理論支持,，其與計(jì)算機(jī)的實(shí)際相結(jié)合,，構(gòu)成了計(jì)算機(jī)科學(xué)中最基礎(chǔ)的理論。計(jì)算機(jī)問題歸根結(jié)底是數(shù)學(xué)問題,，將計(jì)算機(jī)問題抽象成數(shù)學(xué)問題,，是一種合適的解決方式。
隨著互聯(lián)網(wǎng)行業(yè)的快速發(fā)展,，作為其支柱的計(jì)算機(jī)行業(yè)越來越受到人們重視,。然而，人們更加注重程序結(jié)果而不是算法,，更疏于關(guān)心數(shù)據(jù)結(jié)構(gòu),。
本文提出了對(duì)算法設(shè)計(jì)和數(shù)據(jù)結(jié)構(gòu)的離散性體現(xiàn)的思路,，給抽象解決計(jì)算機(jī)問題做一種具體化解釋，以期給讀者建立一種從連續(xù)性到離散性的思維,。
1算法
本節(jié)主要以算法來表述計(jì)算機(jī)中的離散性問題,。本節(jié)概括了算法的基本概念，并以兩個(gè)算法設(shè)計(jì)的方法來表述離散性的表現(xiàn),。該節(jié)算法均以C語言描述,。
1.1算法的基本概念
算法(algorithm)是指解題方案的準(zhǔn)確而完整的描述，是一系列解決問題的清晰指令,，算法代表著用系統(tǒng)的方法描述解決問題的策略機(jī)制［1］,。也就是說，能夠?qū)σ欢ㄒ?guī)范的輸入,，在有限時(shí)間內(nèi)獲得所要求的輸出,。
當(dāng)然，對(duì)于流程型的程序確實(shí)對(duì)算法的要求不高,，但對(duì)于人工智能,、人機(jī)交互、圖形圖像識(shí)別,、音視頻識(shí)別,、虛擬現(xiàn)實(shí)、現(xiàn)實(shí)增強(qiáng),、社會(huì)工程學(xué),、數(shù)據(jù)挖掘、大數(shù)據(jù)分析,、大型網(wǎng)絡(luò)拓?fù)?、云?jì)算等領(lǐng)域來說，算法是其關(guān)鍵,。
現(xiàn)在流行于手機(jī)的各種美圖軟件中,，亦存在較不錯(cuò)的算法設(shè)計(jì)。軟件如何識(shí)別出人臉,？如何分析眼睛,、鼻子、嘴巴等的位置,？如何對(duì)其進(jìn)行一定的“美圖”而不至于讓人無法分辨,？
由計(jì)算機(jī)科學(xué)之父、人工智能之父阿蘭·圖靈(Alan Turing)帶領(lǐng)的小組,，在二戰(zhàn)中幫助盟軍設(shè)計(jì)了破譯德國(guó)的密碼系統(tǒng)Enigma的機(jī)器,。設(shè)計(jì)機(jī)器的過程，可以稱作設(shè)計(jì)算法的過程,。圖靈實(shí)際是領(lǐng)導(dǎo)小組成員設(shè)計(jì)出一個(gè)快速解密德國(guó)納粹密碼系統(tǒng)的算法,，并為這個(gè)算法設(shè)計(jì)了機(jī)器,。
可見，算法其實(shí)是程序的根本,。世界頂尖的科技企業(yè)和高等院校進(jìn)行的各種科學(xué)性研究,，只要涉及計(jì)算機(jī)或與程序相關(guān)，其中一大重點(diǎn)便是在研究算法,。無論對(duì)于多么龐大的一個(gè)系統(tǒng),，設(shè)計(jì)其算法是最基礎(chǔ)也是關(guān)鍵的第一步。
1.2算法體現(xiàn)的離散性
算法設(shè)計(jì)中可以體現(xiàn)出計(jì)算機(jī)科學(xué)中常見的不連續(xù)的特性,，即離散性,。
1.2.1算法設(shè)計(jì)常用的方法
算法設(shè)計(jì)的方法有很多，亦有很多相關(guān)文獻(xiàn),。此處主要介紹最簡(jiǎn)單的兩種方法［2］,，并在后面以此為例,。
?。?）遞推法：遞推是序列計(jì)算機(jī)中的一種常用算法。它是按照一定的規(guī)律來計(jì)算序列中的每個(gè)項(xiàng),，通常是通過計(jì)算機(jī)前面的一些項(xiàng)來得出序列中的指定項(xiàng)的值,。其思想是把一個(gè)復(fù)雜的龐大的計(jì)算過程轉(zhuǎn)化為簡(jiǎn)單過程的多次重復(fù)，該算法利用了計(jì)算機(jī)速度快和不知疲倦的機(jī)器特點(diǎn),。
?。?）遞歸法：程序調(diào)用自身的編程技巧稱為遞歸(recursion)。一個(gè)過程或函數(shù)在其定義或說明中有直接或間接調(diào)用自身的一種方法,，它通常把一個(gè)大型復(fù)雜的問題層層轉(zhuǎn)化為一個(gè)與原問題相似的規(guī)模較小的問題來求解,，遞歸策略只需少量的程序就可描述出解題過程所需要的多次重復(fù)計(jì)算，大大地減少了程序的代碼量,。遞歸的能力在于用有限的語句來定義對(duì)象的無限集合,。一般來說，遞歸需要有邊界條件,、遞歸前進(jìn)段和遞歸返回段,。當(dāng)邊界條件不滿足時(shí)，遞歸前進(jìn),；當(dāng)邊界條件滿足時(shí),，遞歸返回。
1.2.2兩種方法的離散性體現(xiàn)
遞推法中,，計(jì)算機(jī)用一種比較“傻”的方法來進(jìn)行一個(gè)復(fù)雜的運(yùn)算,。如算法1，以一個(gè)求最大值的算法來解釋,。
算法1求最大值
int max(int *array, int size)
{
int mval = *array;
int i;
for (i = 1; i < size; i++)
if (array［i］ > mval)
mval = array［i］;
return mval;
}
可見對(duì)于計(jì)算機(jī)來說,，它會(huì)不斷地用已知最大的數(shù)去和數(shù)組中下一個(gè)數(shù)字作比較,，直到結(jié)束，即使有很多很多數(shù)字,。而人類比較數(shù)字大小的方式就不同了,，如果數(shù)字非常多，則可能會(huì)先看看數(shù)字都是幾位的,，挑出位數(shù)最高的,，如果不止一個(gè),則再去逐個(gè)比較。這是一種連續(xù)性的思維模式,。這正是人類習(xí)慣的連續(xù)性思維,，初等數(shù)學(xué)都是建立在連續(xù)的基礎(chǔ)上，也亦有了幾何的出現(xiàn),。然而對(duì)于計(jì)算機(jī)來說,，要有這種連續(xù)的思維是很困難的，要設(shè)計(jì)出更加復(fù)雜的算法,，才能“模擬”出人類的這種連續(xù)性思維,。當(dāng)然，亦有可能是因?yàn)槿祟惖拇竽X這個(gè)“CPU”比較高級(jí),，自身的算法就足夠復(fù)雜,，所以人類才擁有連續(xù)性思維。對(duì)于設(shè)計(jì)出更復(fù)雜的算法和更快速的計(jì)算機(jī)來“模擬”人腦的思維模式,，也有相關(guān)研究,，亦有不少相關(guān)文獻(xiàn)，這不是本文重點(diǎn),。
遞歸法有時(shí)可以簡(jiǎn)化算法,，以求兩個(gè)自然數(shù)的最大公約數(shù)為例，如算法2,，其改用遞歸算法后如算法3,。
算法2求最大公約數(shù)
void swapi(int *x, int *y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
int gcd(int m, int n)
{
int r;
do
{
if (m < n)
swapi(&m, &n);
r=m%n;
m=n;
n=r;
} while (r);
return m;
}
算法3遞歸法求最大公約數(shù)
int gcd(int a,int b)
{
if(a%b)
return gcd(b,a%b);
return b;
}
形象地說遞歸法就是“自己調(diào)用自己”。一種離散性的表現(xiàn)與之前的例子類似,，這里不再重復(fù),。這里講的是程序運(yùn)行表現(xiàn)的離散性。計(jì)算機(jī)會(huì)在棧中運(yùn)行程序,，棧的特點(diǎn)就是“后進(jìn)先出”,。在運(yùn)行這個(gè)遞歸的算法時(shí)，需要返回值時(shí)返回一個(gè)“自己”,，只不過參數(shù)不同,。直到返回一個(gè)確定的值，再層層返回，如圖1所示,。
可見,，對(duì)于該算法，計(jì)算機(jī)每遞歸計(jì)算一次,，就要向內(nèi)存中Push一次,，直到計(jì)算完成，再一次一次Pop出,。這是一種計(jì)算的離散性體現(xiàn),，這亦不會(huì)是人類的連續(xù)性的思維方式。
2數(shù)據(jù)結(jié)構(gòu)
本節(jié)主要以數(shù)據(jù)結(jié)構(gòu)來表述計(jì)算機(jī)中的離散性問題,。本節(jié)概括了數(shù)據(jù)結(jié)構(gòu)的基本概念,，并提出了數(shù)據(jù)結(jié)構(gòu)的離散性的基本理解。
2.1數(shù)據(jù)結(jié)構(gòu)的基本概念
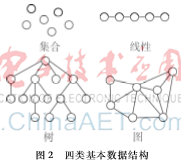
數(shù)據(jù)結(jié)構(gòu)是計(jì)算機(jī)科學(xué)的經(jīng)典學(xué)科,。字面上來說,，就是研究數(shù)據(jù)元素之間的結(jié)構(gòu)關(guān)系。根據(jù)數(shù)據(jù)元素之間關(guān)系的不同特性,，一般來說可分為四類基本結(jié)構(gòu)：集合,、線性結(jié)構(gòu)、樹形結(jié)構(gòu),、圖狀結(jié)構(gòu)或網(wǎng)狀結(jié)構(gòu)［3］,，如圖2所示,。這正是數(shù)據(jù)結(jié)構(gòu)的元素具有的離散性特征,。
Nicklaus Wirth憑借“算法+數(shù)據(jù)結(jié)構(gòu)=程序”這一公式獲得了計(jì)算機(jī)科學(xué)領(lǐng)域最高獎(jiǎng)——圖靈獎(jiǎng)。這已足以可見數(shù)據(jù)結(jié)構(gòu)的重要性,。
數(shù)據(jù)結(jié)構(gòu)主要討論的是相互之間存在一種或多種特定關(guān)系的數(shù)據(jù)元素的集合,。在任何問題中，數(shù)據(jù)元素都不是孤立存在的,，而是在它們之間存在著某種關(guān)系,，這種數(shù)據(jù)元素相互之間的關(guān)系稱之為結(jié)構(gòu)(structure)。而離散數(shù)學(xué)與數(shù)據(jù)結(jié)構(gòu)有千絲萬縷的聯(lián)系,，很多大學(xué)的計(jì)算機(jī)專業(yè)將離散數(shù)學(xué)作為數(shù)據(jù)結(jié)構(gòu)的先導(dǎo)課程,。
2.2數(shù)據(jù)結(jié)構(gòu)的離散性
離散數(shù)學(xué)中的圖論可以說就是對(duì)數(shù)據(jù)結(jié)構(gòu)的抽象，這方面的學(xué)術(shù)文獻(xiàn)相當(dāng)豐富,。這里僅對(duì)其做一個(gè)較為簡(jiǎn)單,、通俗的理解說明。
對(duì)于集合結(jié)構(gòu),，如圖2所示,，其元素本身就是離散的、無關(guān)的。
對(duì)于線性結(jié)構(gòu)的離散性是顯而易見的,。前文在介紹算法的離散性時(shí)提到棧的應(yīng)用,，可見其離散性。其余線性結(jié)構(gòu)類似,。
樹形結(jié)構(gòu)和圖形結(jié)構(gòu)也很好理解,，每個(gè)元素本來是獨(dú)立存在，由于元素之間滿足了某種關(guān)系使其變成了樹形或圖形結(jié)構(gòu),，自然這種關(guān)系是離散的,，不連續(xù)的。
實(shí)際上,，離散數(shù)學(xué)與數(shù)據(jù)結(jié)構(gòu)的關(guān)系是最為緊密的,。離散數(shù)學(xué)中的圖論實(shí)際就是研究一些復(fù)雜的數(shù)據(jù)元素之間的關(guān)系［4］。一些離散數(shù)學(xué)中的理論應(yīng)用在計(jì)算機(jī)中,，實(shí)現(xiàn)了一些難以解決的問題或優(yōu)化了一些原本不恰當(dāng)?shù)姆椒?，例如哈夫?Huffman)樹解決了壓縮編碼的問題。
3離散數(shù)學(xué)與數(shù)字電子
本節(jié)將介紹離散數(shù)學(xué)的一些概念,，并指出其與數(shù)字電子（主要是數(shù)字信號(hào)）的關(guān)系,。
3.1離散數(shù)學(xué)的基本概念
離散數(shù)學(xué)是數(shù)學(xué)的幾個(gè)分支的總稱，是研究基于離散空間而不是連續(xù)的數(shù)學(xué)結(jié)構(gòu),。與光滑變化的實(shí)數(shù)不同,，離散數(shù)學(xué)的研究對(duì)象，例如整數(shù),、圖和數(shù)學(xué)邏輯中的命題［5］,，不是光滑變化的，而是擁有不等,、分立的值［6］,。因此離散數(shù)學(xué)不包含微積分和分析等“連續(xù)數(shù)學(xué)”的內(nèi)容。離散對(duì)象經(jīng)?？梢杂谜麛?shù)來枚舉,。更一般地，離散數(shù)學(xué)被視為處理可數(shù)集合（與整數(shù)子集基數(shù)相同的集合,，包括有理數(shù)集但不包括實(shí)數(shù)集）的數(shù)學(xué)分支［7］,。但是，“離散數(shù)學(xué)”不存在準(zhǔn)確且普遍認(rèn)可的定義［8］,。實(shí)際上,，離散數(shù)學(xué)經(jīng)常被定義為不包含連續(xù)變化量及相關(guān)概念的數(shù)學(xué)，甚少被定義為包含什么內(nèi)容的數(shù)學(xué),。
3.2數(shù)字電子的基本概念與離散性
數(shù)字電子是一門學(xué)科,，與計(jì)算機(jī)學(xué)科相互交叉。此處僅以其數(shù)字信號(hào)的基本概念解釋其離散性。
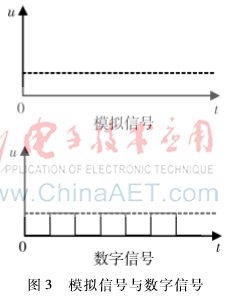
數(shù)字信號(hào)同模擬信號(hào)相對(duì),，模擬信號(hào)是指時(shí)間和數(shù)值都連續(xù)的一組信號(hào),，而數(shù)字信號(hào)是指時(shí)間和數(shù)值都是離散的一組信號(hào)，如圖3所示,。從圖3可以看出,，這種連續(xù)性與離散性是非常明顯的。從數(shù)學(xué)上來說,，連續(xù),，意味著其微積分有意義。顯然,，對(duì)離散的信號(hào)這是沒有意義的,。這里不再深究。
4計(jì)算機(jī)中的離散性問題
本節(jié)主要介紹二進(jìn)制體現(xiàn)出來的離散性問題,，并歸結(jié)出計(jì)算機(jī)中的離散性問題基本都與計(jì)算機(jī)采用的二進(jìn)制的性質(zhì)有關(guān),。
4.1二進(jìn)制
計(jì)算機(jī)中以二進(jìn)制進(jìn)行存儲(chǔ)和運(yùn)算，這涉及邏輯數(shù)學(xué)的一些概念,。實(shí)際上,，邏輯運(yùn)算亦能體現(xiàn)離散性。這與計(jì)算機(jī)的運(yùn)算是有映射關(guān)系的,。
4.1.1基本概念
二進(jìn)制是逢2進(jìn)位的進(jìn)位制,。“0”,、“1”是基本算符?，F(xiàn)代的電子計(jì)算機(jī)技術(shù)全部采用的是二進(jìn)制，因?yàn)樗皇褂谩?”,、“1”這兩個(gè)數(shù)字符號(hào),，非常簡(jiǎn)單方便,，易于用電子方式實(shí)現(xiàn)［9］,。
由于人類習(xí)慣使用十進(jìn)制，可以這樣表述二進(jìn)制：二進(jìn)制數(shù)的每一位數(shù)的位權(quán)（理解為“1”能有多“大”）為2n-1（n為位數(shù)）,。這樣可以充分理解二進(jìn)制數(shù)的“大小”,。
4.1.2體現(xiàn)
計(jì)算機(jī)是一個(gè)只認(rèn)識(shí)“0”、“1”的機(jī)器,，對(duì)于人類來說很容易理解的信息（如圖片,、音視頻）對(duì)于計(jì)算機(jī)來說卻不能直接理解。所以計(jì)算機(jī)本身就要通過離散的數(shù)據(jù)來“認(rèn)識(shí)世界”,。
計(jì)算機(jī)所處理的對(duì)象都是離散的數(shù)據(jù),。所謂離散的數(shù)據(jù)，可以理解為從本質(zhì)上說計(jì)算機(jī)只能處理“0”、“1”組成的二進(jìn)制的數(shù)據(jù),。計(jì)算機(jī)要進(jìn)行圖像,、文字、聲音等數(shù)據(jù)的處理,，必須將其轉(zhuǎn)換成二進(jìn)制的數(shù)據(jù)表示,，
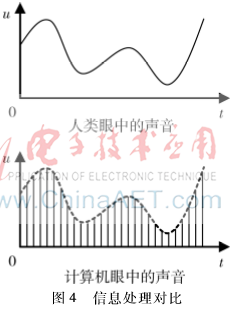
也就是說進(jìn)行離散化處理。只如音頻處理,，只有將連續(xù)變化的聲音轉(zhuǎn)換成二進(jìn)制的數(shù)據(jù)來表示,，這樣計(jì)算機(jī)才能進(jìn)行處理。
圖4所示就是計(jì)算機(jī)將音頻信息離散化的方法,。離散化得越“細(xì)”,，就越能還原聲音的原來面貌?！ ?/p>
4.2簡(jiǎn)要分析
計(jì)算機(jī)采用的二進(jìn)制使得計(jì)算機(jī)處理問題具有離散性的特征,。前面所述的算法設(shè)計(jì)與數(shù)據(jù)結(jié)構(gòu)的離散性體現(xiàn)，都可以通過二進(jìn)制來解釋,。這涉及一些比較靠近計(jì)算機(jī)底層的理論,，這里不再深究。
5結(jié)論
本文以探究離散數(shù)學(xué)的方式淺析了計(jì)算機(jī)的離散性問題,，特別是在算法設(shè)計(jì)與數(shù)據(jù)結(jié)構(gòu)上,，并最終說明計(jì)算機(jī)采用的二進(jìn)制是計(jì)算機(jī)離散性問題的一個(gè)關(guān)鍵。
隨著計(jì)算機(jī)科學(xué)的發(fā)展和實(shí)際需求的日益增長(zhǎng),，計(jì)算機(jī)的離散性越來越受到相關(guān)領(lǐng)域的關(guān)注和重視,，相信這是一個(gè)極具價(jià)值的研究領(lǐng)域，值得更深一步的探索,。
參考文獻(xiàn)
?。?］ 譚浩強(qiáng). C程序設(shè)計(jì)［M］. 北京: 清華大學(xué)出版社,2005.
［2］ ROGERS H. Theory of recursive functions and effective computability［M］. Cambridge: The MIT Press, 1987.
?。?］ 嚴(yán)蔚敏,吳偉民. 數(shù)據(jù)結(jié)構(gòu): C語言版［M］. 北京: 清華大學(xué)出版社,2007.
?。?］ 屈婉玲,耿素云,張立昂. 離散數(shù)學(xué)［M］. 北京: 清華大學(xué)出版社,2008.
［5］ JOHSONBAUGH R. Discrete mathematics ［M］. Upper Saddle River： Prentice Hall, 2008.
?。?］ WEISSTEIN E. Discrete mathematics ［EB/OL］. (2016-06-19)［2016-07-16］ http://mathworld.wolfram.com/DiscreteMathematics.html.
?。?］ BIGGS N. Discrete mathematics ［M］. Oxford: Oxford University Press,2002.
［8］ HOPKINS B. Resources for teaching discrete mathematics ［M］. Washington D.C.: Mathematical Association of America,2008.
?。?］ 康華光. 電子技術(shù)基礎(chǔ): 數(shù)字部分（第6版）［M］. 北京: 高等教育出版社,2014.