文獻(xiàn)標(biāo)識(shí)碼: A
文章編號(hào): 0258-7998(2014)04-0103-03
隨著計(jì)算機(jī)及數(shù)字信號(hào)處理技術(shù)的發(fā)展,全數(shù)字接收機(jī)[1]在衛(wèi)星通信技術(shù)中得到了廣泛應(yīng)用。由于多普勒頻移及移動(dòng)終端與衛(wèi)星之間長(zhǎng)的傳播時(shí)延,不可避免地存在采樣時(shí)刻偏差,導(dǎo)致接收端數(shù)據(jù)樣點(diǎn)并不一定在最佳采樣點(diǎn)上,從而造成了誤碼。
然而在衛(wèi)星通信系統(tǒng)中,信號(hào)調(diào)制載波頻率存在較大偏移[2],這將對(duì)數(shù)據(jù)的正確解調(diào)產(chǎn)生嚴(yán)重的影響。為了解決這個(gè)問題,本文在Gardner改進(jìn)算法E-Gardner(Evolved Gardner)[3]的基礎(chǔ)上提出了一種用于數(shù)字通信接收端時(shí)鐘誤差檢測(cè)模塊的抗載波偏差算法AC-Gardner(Anti Carrier Gardner)。該算法可以在載波偏差存在的情況下工作,并表現(xiàn)出接近無載波偏差時(shí)的性能,提高了原算法的可靠性和準(zhǔn)確度。
本文簡(jiǎn)單介紹了基于全數(shù)字接收的改進(jìn)定時(shí)同步環(huán)路模型,并對(duì)所提出的AC-Gardner算法作了詳細(xì)的原理描述和數(shù)學(xué)證明,對(duì)AC-Gardner算法進(jìn)行了仿真,其結(jié)果與E-Gardner算法在S曲線斜率、誤碼率等性能方面做了比較。
1 AC-Gardner誤差檢測(cè)算法

圖1為改進(jìn)的定時(shí)同步環(huán)路模型,主要由插值濾波器、時(shí)鐘誤差檢測(cè)器TED(Timing Error Detector)、環(huán)路濾波器及定時(shí)控制器四部分組成。該改進(jìn)模型與傳統(tǒng)定時(shí)同步環(huán)路[4]的區(qū)別在于TED模塊中不僅采用E-Gardner算法,而且還增加了載波偏差估計(jì)與補(bǔ)償部分。該模塊既能實(shí)現(xiàn)無載波偏差信號(hào)的定時(shí)誤差檢測(cè),也能對(duì)含載波偏差的基帶信號(hào)先進(jìn)行定時(shí)誤差檢測(cè),再進(jìn)行載波頻偏與相偏估計(jì),最后與數(shù)字下變頻后的基帶信號(hào)進(jìn)行復(fù)數(shù)乘法運(yùn)算得到校正信號(hào)。
根據(jù)該定時(shí)環(huán)路模型,接收的信號(hào)經(jīng)下變頻后得到:
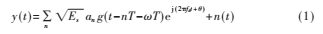
其中,an為正交QPSK符號(hào)的發(fā)送序列,an=exp(j·in),in=0,1,2,3,Es=1為符號(hào)能量,n為符號(hào)序列,T為碼元寬度,為從發(fā)射機(jī)到接收機(jī)的歸一化傳播時(shí)延,g(t)為升余弦脈沖,fd為多普勒頻移,收發(fā)載波固定相差,n(t)為加性復(fù)高斯白噪聲。
對(duì)y(t)采樣并使其進(jìn)入定時(shí)同步環(huán)路得到的E-Gardner算法的表達(dá)式為:

當(dāng)定時(shí)同步環(huán)路進(jìn)入穩(wěn)定狀態(tài)后,對(duì)連續(xù)的QPSK信號(hào)經(jīng)本地固定時(shí)鐘采樣及插值濾波器后,可以得到每個(gè)符號(hào)的最佳采樣點(diǎn)。假設(shè)發(fā)送信號(hào)的幅度相同,且在傳播過程中衰減一致,則接收信號(hào)最佳采樣點(diǎn)的幅值大約相等。于是得到:
![PZY$K}B21[Y{BO7Y6`]B{XW.png PZY$K}B21[Y{BO7Y6`]B{XW.png](http://files.chinaaet.com/images/2017/01/23/6362079752277900005952989.png)
因此,多普勒頻移fd對(duì)TED模塊定時(shí)誤差檢測(cè)性能的影響不是線性的,而是周期性的,如圖2所示。
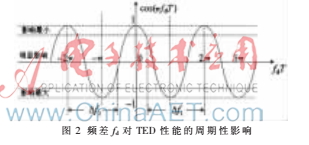
為了消除多普勒頻移對(duì)TED模塊性能的影響,必須將多普勒頻率搬移到其對(duì)頻偏幾乎無影響的區(qū)間,即只需將多普勒頻移fd搬移至2/T的整數(shù)倍即可,所以必須計(jì)算出搬移頻率的大小。
由于余弦函數(shù)![RP}_KKW6$CE%%I_Z1@]W}IY.jpg RP}_KKW6$CE%%I_Z1@]W}IY.jpg](http://files.chinaaet.com/images/2017/01/23/6362079755504000005174498.jpg) 為周期,于是整個(gè)區(qū)間上的搬移頻率
為周期,于是整個(gè)區(qū)間上的搬移頻率![YFJW{Q)1I][U%J5_)D6TV[D.jpg YFJW{Q)1I][U%J5_)D6TV[D.jpg](http://files.chinaaet.com/images/2017/01/23/6362079759304700001757205.jpg) 為:
為:
![CAW0K36(UE7S5X495~P7`]H.png CAW0K36(UE7S5X495~P7`]H.png](http://files.chinaaet.com/images/2017/01/23/6362079754395100009525693.png)
因而,將計(jì)算的搬移頻率與數(shù)字下變頻后的基帶信號(hào)進(jìn)行復(fù)數(shù)乘法運(yùn)算,最終得到矯正的基帶信號(hào)。
2 仿真結(jié)果及性能分析
信道環(huán)境:用Matlab在基于鄉(xiāng)村陰影環(huán)境的Corazza信道模型下對(duì)AC-Gardner算法的性能進(jìn)行仿真,仿真參數(shù)配置表如表1所示。

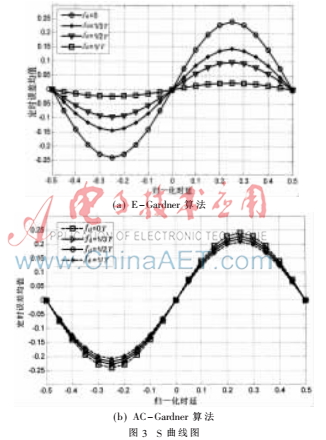
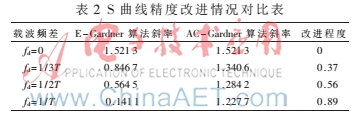
對(duì)于一個(gè)定時(shí)誤差檢測(cè)算法,S曲線可以直接反映算法的性能好壞。通常,S曲線越平滑且越陡峭,對(duì)應(yīng)的算法性能就越好。所以為了進(jìn)一步驗(yàn)證AC-Gardner算法的性能,需進(jìn)行開環(huán)仿真。圖3為E-Gardner算法和AC-Gardner算法存在載波偏差時(shí)的S曲線圖。按照以S曲線在零點(diǎn)處的斜率代表精確度這個(gè)標(biāo)準(zhǔn)驗(yàn)證AC-Gardner算法的精度性能,由前面推導(dǎo)得知,載波頻差fd對(duì)TED性能呈周期性影響。所以為了簡(jiǎn)便起見,只需統(tǒng)計(jì)兩種算法在載波頻差fd∈[0,1/T]的精確度,表2為其S曲線精度改進(jìn)情況對(duì)比表。從該表中知道,存在載波偏差時(shí),與E-Gardner算法相比,AC-Gardner算法精度性能約提升37%~89%左右。
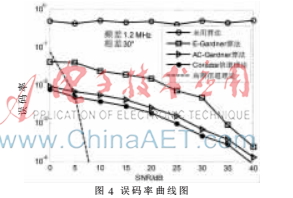
AC-Gardner算法性能可用接收端QPSK信號(hào)的誤碼率來分析,從圖4仿真結(jié)果可知,當(dāng)載波頻偏fd=1.2 MHz時(shí),隨著信噪比的增加,盡管誤碼率曲線是逼近理想高斯白噪聲信道的,但由于多徑衰落及陰影效應(yīng),信號(hào)有很強(qiáng)的衰落,存在較大的誤碼率。通過對(duì)比發(fā)現(xiàn), AC-Gardner算法誤碼率曲線很貼近Corazza信道理論曲線。當(dāng)信噪比為20 dB時(shí),E-Gardner算法的誤碼率約為1.8×10-2,AC-Gardner算法誤碼率約為2.5×10-3,經(jīng)計(jì)算后者性能提升約8.57 dB。而且,在信噪比[0,40] dB范圍內(nèi),AC-Gardner算法的平均增益約為8.46 dB。因此,當(dāng)信號(hào)中存在載波頻差和相差時(shí), AC-Gardner算法的校正性能較好。
本文提出了一種適用于衛(wèi)星通信數(shù)字接收端TED模塊的AC-Gardner算法,并給出了該算法的數(shù)學(xué)推導(dǎo)過程,同時(shí)在Corazza衛(wèi)星信道環(huán)境下從頻差估計(jì)范圍、S曲線斜率、誤碼率等三方面對(duì)其正確性進(jìn)行了驗(yàn)證。仿真結(jié)果表明,AC-Gardner算法不僅增強(qiáng)了Gardner及其改進(jìn)算法對(duì)抗載波偏差的性能,同時(shí)也繼承了Gardner算法實(shí)現(xiàn)簡(jiǎn)單、硬件消耗較小、對(duì)相位偏差不敏感的特點(diǎn)。所以,AC-Gardner算法能很好地克服衛(wèi)星通信中存在的多普勒偏移及加速度等難點(diǎn),在全數(shù)字解調(diào)尤其是衛(wèi)星移動(dòng)通信系統(tǒng)中有著較高的應(yīng)用價(jià)值。
參考文獻(xiàn)
[1] MARAL G, BOUSQUET M. Satellite communications sys-tems: systems, techniques and technology[M].3rd ed.[S.l.]:Wiley, 2011.
[2] 張公禮.全數(shù)字接收機(jī)理論及技術(shù)[M]. 北京:科學(xué)出版社, 2005.
[3] LIM D. A modified Gardner detector for symbol timing re-covery of M-PSK signals [J]. IEEE Trans. On Communi-cations, 2004,52(10):1643-1647.
[4] Chen Yang, Wang Yongqu. The design of a symbol timingsynchronization system for all digital receiver[J]. Microcom-puter Information, 2010(23):071.
[5] 劉強(qiáng), 陳西宏, 周進(jìn). 對(duì)流層散射多徑信道估計(jì)性能分析[J]. 電子技術(shù)應(yīng)用, 2011,37(3):94-97.
[6] 付永明,朱江,琚瑛玨. Gardner 定時(shí)同步環(huán)路參數(shù)設(shè)計(jì)及性能分析[J].通信學(xué)報(bào), 2012,33(6):191-198.
[7] 唐筠. 同步頭輔助的 MPSK 信號(hào)高精度頻偏估計(jì)[J].微型機(jī)與應(yīng)用, 2011,30(20):65-67.

