傳統(tǒng)微弱信號檢測方法在檢測信噪比極低信號時效果很差[1]，而Duffing振子混沌系統(tǒng)由于具有對初值極端敏感,、對噪聲具有較好免疫力等優(yōu)點(diǎn),，在檢測微弱信號時表現(xiàn)出良好效果。作為一種新的微弱信號檢測方法,，混沌振子方法不是消除噪聲,，而是從噪聲背景中提取信號，針對其獨(dú)特性可將其應(yīng)用到實(shí)際工程中,，包括心電信號檢測[2],、GPS信號捕獲[3]、機(jī)電設(shè)備早期故障診斷[4]等方面,。

　　本文在分析Duffing非線性動力學(xué)系統(tǒng)運(yùn)動特性基礎(chǔ)上,，針對Duffing振子微弱信號檢測方法存在的問題,，提出基于偽哈密頓量的變尺度Duffing振子弱信號檢測方法。

1 理論分析

　　1.1 基于Duffing方程微弱信號檢測原理

　　選用連續(xù)動力學(xué)系統(tǒng)中Duffing振子作為研究對象,，Duffing方程標(biāo)準(zhǔn)形式為[5]：

　　式(1)中,，k為阻尼比，r為策動力振幅,，w為策動力角頻率,。

　　式(1)加入待測信號并寫成狀態(tài)方程形式為：

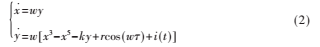
　　上式中為外部引入的湮沒在噪聲中的微弱正弦信號，h為待測正弦信號幅度,，為待測信號與Duffing系統(tǒng)內(nèi)置周期策動力信號頻率差,， 為待測信號初始相位， n(t)為待測信號中混有的噪聲,。

　　在Simulink仿真環(huán)境下由式(2)即可構(gòu)造出傳統(tǒng)的混沌振子檢測微弱信號的檢測模型。

　　1.2 Duffing系統(tǒng)混沌判據(jù)

　　傳統(tǒng)上用Lyapunov特性指數(shù)(LCE)確定系統(tǒng)從混沌態(tài)躍變到周期態(tài)的相變閾值rd,，用梅爾尼科夫(Melnikov)函數(shù)進(jìn)行理論計(jì)算得到混沌閾值rc的粗略估計(jì)值[6],。Duffing方程的Melnikov函數(shù)形式如下：

　　1.3 高頻參數(shù)待測信號尺度變換

　　式(4)說明混沌閾值與周期策動力頻率有關(guān)，當(dāng)k=0.5時,，其關(guān)系如圖1所示,。可見當(dāng)系統(tǒng)阻尼比k固定時,，在低頻段只需要很小幅度的驅(qū)動力就會使系統(tǒng)產(chǎn)生混沌,，而在高頻段時則需要較大的驅(qū)動力。另一方面,，Duffing系統(tǒng)只有在低頻參數(shù)條件下有較好的動態(tài)特性和檢測效果,，且Duffing振子檢測信號時，不同頻率待測信號對應(yīng)的相變閾值也不同,，如果每次檢測過程都要搜索相變閾值,，將大大增加檢測復(fù)雜度。

　　在處理工程信號時,，文章對待測信號進(jìn)行二次采樣,，即引入變尺度系數(shù)R，對待測信號進(jìn)行頻率/時間尺度變換,。若待測信號角頻率為w,，其采樣頻率為fs，則數(shù)值計(jì)算的步長為dt=1/fs,。對檢測系統(tǒng)引入變尺度系數(shù)R相當(dāng)于將信號的時間間隔增大了R倍,，相應(yīng)的信號角頻率被壓縮R倍后變?yōu)閣/R，此時數(shù)值計(jì)算步長變?yōu)閐t′=Rdt=R/fs,。

2 自相關(guān)與小波變換聯(lián)合去噪

　　設(shè)已知頻率待測信號為：x(t)=s(t)+n(t),s(t)是周期信號,，n(t)是均值為零的高斯白噪聲，信號自相關(guān)輸出為：

　　式(7)中，n′(t)是相關(guān)信號中混有的噪聲,。

　　實(shí)際中由于積分時間不可能無限長,，噪聲只能得到一定程度的抑制[7]，剩余噪聲可通過對相關(guān)后信號進(jìn)行小波閾值變換進(jìn)一步削弱,。

　　小波閾值消噪過程中,，信號經(jīng)過小波變換后，可以認(rèn)為由信號產(chǎn)生的小波系數(shù)包含有信號的重要信息,，其幅值大,，但數(shù)目較少，而噪聲對應(yīng)的小波系數(shù)幅值小,。因此,，通過在不同尺度上選取一合適閾值，并將小于該閾值的小波系數(shù)置零,，而保留大于該閾值的小波系數(shù),，從而使信號中的噪聲得到有效抑制。最后進(jìn)行逆小波變換,，得到去噪后的重構(gòu)信號,。

3 Duffing系統(tǒng)偽哈密頓量

　　考慮平面微分動力系統(tǒng)：

　　則稱式(8)為平面哈密頓系統(tǒng)，其中H(x1,x2)稱為該系統(tǒng)的哈密頓量,。

　　對于式(1)Duffing方程,，不考慮阻尼項(xiàng)和策動力的影響，可以改寫為：

　　實(shí)際應(yīng)用中阻尼項(xiàng)和策動力對于系統(tǒng)的哈密頓量有一定影響,，但對系統(tǒng)能量分布幾乎沒有影響,，此時的哈密頓量為偽哈密頓量(PH)[8]。圖2為Duffing系統(tǒng)PH值分布情況,，兩個鞍點(diǎn)處PH值最低,，系統(tǒng)混沌特性越明顯PH值越低，大尺度周期狀態(tài)時PH值最高,。

　　用下式構(gòu)造Duffing系統(tǒng)平均哈密頓量(APH),。

　　式(17)中，N為動力系統(tǒng)的時間序列長度,，i為系統(tǒng)的第i個狀態(tài),。圖3是策動力為rcos(t)時，策動力幅值變化時Duffing系統(tǒng)APH值變化情況,?；趫D3中APH值階躍型跳變特性來設(shè)定閾值，進(jìn)而判斷是否存在微弱信號,。

4 仿真測試和分析

　　基于前面分析,，提出如圖4所示基本原理檢測低信噪比微弱信號,。

　　仿真環(huán)境下為試驗(yàn)待測信號，n(t)為均值為零的高斯白噪聲,。檢測系統(tǒng)相關(guān)參數(shù)為：系統(tǒng)初始狀態(tài)(x,0)=(0,0),， k=0.5, fs=10 000 Hz，h=0.000 3 V,w=200 rad/s,，w=0,采用四階Runge-Kutta方法對Duffing方程進(jìn)行數(shù)值求解,，數(shù)值計(jì)算步長為:

　　dt=1/fs=0.000 1         (13)

　　引入變尺度系數(shù)R=200,變換后信號角頻率w′=1 rad/s，則二次采樣頻率fs′=fs/R=500 Hz,，數(shù)值計(jì)算步長dt′=Rdt=0.02,。

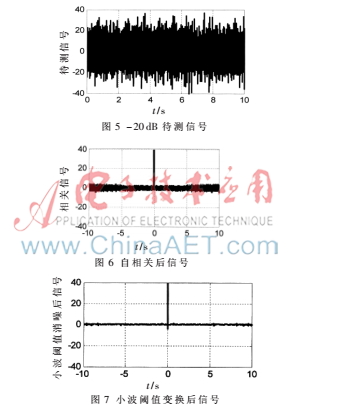
　　圖5~圖7分別為-20 dB待測信號及此信號先后經(jīng)過自相關(guān)器和小波閾值變換后的輸出，從圖就能直觀看出兩次去噪過程均提高了待測信號信噪比,。

　　本文算法采用信噪比改善因子SNIR衡量去噪效果,，其計(jì)算式如下：

　　SNIR=SNRout-SNRin  (14)

　　式中：SNRin為輸入信噪比，SNRout為輸出信噪比,。

　　圖8為不同輸入信噪比條件下的SNIR值,，由圖可知，通過相關(guān)運(yùn)算可以抑制部分噪聲,，對相關(guān)后信號進(jìn)行小波閾值變換，信噪比又有一定程度改善,，且在一定范圍內(nèi),，輸入信號信噪比越低，這種改善越明顯,，證明了本文方法的有效性,。

　　若系統(tǒng)APH值用T表示，仿真得到閾值rd=0.827 856 7,，數(shù)次驗(yàn)證后選APH值判決系統(tǒng)狀態(tài)的門限值為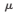=0.35,，則有：

　　實(shí)驗(yàn)中取t=100 時Lmax值作為最終系統(tǒng)狀態(tài)穩(wěn)定的Lmax值，實(shí)驗(yàn)得到表1~表3結(jié)果,。

　　從表1~表3數(shù)據(jù)看出,，基于偽哈密頓量和Lyapunov指數(shù)的系統(tǒng)狀態(tài)判別方法結(jié)果是一致的。另外,，混沌檢測系統(tǒng)能夠檢測的信噪比門限為-10.5 dB, 相關(guān)-混沌檢測系統(tǒng)能夠檢測的信噪比門限為-35.5 dB,，相關(guān)與小波變換聯(lián)合-混沌檢測系統(tǒng)能夠檢測的信噪比門限為-39 dB，由此可見本文檢測算法的有效性和優(yōu)越性,。

　　實(shí)驗(yàn)得到,，利用系統(tǒng)APH值判別狀態(tài)的平均計(jì)算時間為0.62 s，利用系統(tǒng)狀態(tài)穩(wěn)定時Lmax值判別狀態(tài)的平均計(jì)算時間為6.7 s,?？梢?，APH值算法計(jì)算效率明顯高于Lyapunov特性指數(shù)算法。

　　本文提出基于偽哈密頓量的變尺度Duffing振子弱信號檢測方法,，通過頻率/時間尺度變換把高頻信號轉(zhuǎn)換為固定角頻率1 rad/s的信號,，方便了設(shè)置系統(tǒng)相變閾值，克服了傳統(tǒng)方法低頻參數(shù)信號的限制,；搭建相關(guān)與小波閾值變換的聯(lián)合去噪系統(tǒng),極大程度地改善了信噪比,，避免了噪聲對檢測結(jié)果的不利影響；構(gòu)造Duffing系統(tǒng)偽哈密頓量實(shí)時地表征系統(tǒng)動力學(xué)行為,，解決了定量判斷系統(tǒng)狀態(tài)時計(jì)算量大,，效率低的難題。仿真分析驗(yàn)證了本文所提檢測方法的有效性和優(yōu)越性,。

　　參考文獻(xiàn)

　　[1] 高科, 孫晶華. 微弱信號檢測方法研究[J]. 微型機(jī)與應(yīng)用,2011,30(21):67-68.

　　[2] 張紅煊, 朱貽盛,牛金海,等. 異常心電節(jié)律VT和VF信號的復(fù)雜性分析[J].物理學(xué)報, 2000,49(8):1416-1422.

　　[3] 黃鵬達(dá), 皮亦鳴.基于混沌振子的微弱GPS信號檢測算法[J]. 電子測量與儀器學(xué)報, 2008,22(4):49-49.

　　[4] 胥永剛,馬海龍,付勝,等.機(jī)電設(shè)備早期故障微弱信號的非線性檢測方法及工程應(yīng)用[J].振動工程學(xué)報, 2011,24(5):529-538.

　　[5] 魏世朋,張?zhí)祢U,白娟,等.用Duffing 振子陣列解調(diào)微弱π/4-DQPSK信號[J].電子技術(shù)應(yīng)用, 2011,37(11):120-124.

　　[6] 楊紅英,葉昊,王桂增,等. Duffing振子的Lyapunov指數(shù)與Floquet指數(shù)研究[J]. 儀器儀表學(xué)報,2008, 29(5):927-932.

　　[7] 李健, 周激流, 孫濤,等.自相關(guān)級聯(lián)混沌振子法實(shí)現(xiàn)隨相弱正弦信號的檢測[J]. 四川大學(xué)學(xué)報 (工程科學(xué)版),2010,42(1):191-195.

　　[8] CHENG D. Stabilization of time-varying pseudo-hamilton-ian systems[C].Control Applications, 2002. Proceedings ofthe 2002 International Conference on. IEEE,2002(2):954-959.