0 引言

　　仿人機器人是機器人研究領(lǐng)域中的一個重要分支,，仿人機器人的步態(tài)行走系統(tǒng)是在以往深入研究仿人行走系統(tǒng)的各項技術(shù)環(huán)節(jié),，以提高仿人機器人行走環(huán)節(jié)的擬人化程度，使其各項功能最大程度地接近人類運動,，從而保證仿人機器人在不同環(huán)境下完成任務(wù)的能力的基礎(chǔ)上提出的,，是步行機器人研究中的一個重要而又關(guān)鍵的技術(shù)。但是仿人機器人的步態(tài)行走系統(tǒng)是一個多變量,、非線性,、強耦合的復(fù)雜動力學(xué)系統(tǒng)，要實現(xiàn)和提高機器人的行走性能,，必須研究實用而有效的步態(tài)控制方法,，實現(xiàn)機器人的實時穩(wěn)定步行[1-2]。很多學(xué)者采用較少的變量來獲得仿人機器人的步態(tài)行走軌跡,，將倒立擺模型應(yīng)用于機器人步態(tài)規(guī)劃中,，取得滿意的控制效果[3-5]。

　　本文在深入研究倒立擺模型基礎(chǔ)上,，應(yīng)用PID控制算法對仿人行走系統(tǒng)進行控制,，并在開發(fā)以STM32+CPLD為核心19軸集成運動控制平臺中進行驗證，通過對比理論與原理樣機實驗數(shù)值,，關(guān)節(jié)輸出最大相對誤差為2.25%,，表明了該控制方法的準確性和有效性,。

1 仿人機器人行走問題描述

　　設(shè)計的10自由度仿人行走系統(tǒng)的機構(gòu)模型如圖1所示。

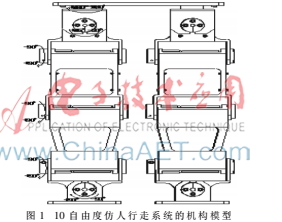
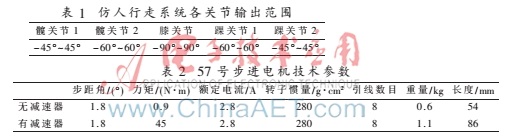
　　采用左右腿對稱的結(jié)構(gòu)方式,。以右腿為例,，其自由度分配為：髖關(guān)節(jié)2個自由度，膝關(guān)節(jié)1個自由度,，踝關(guān)節(jié)2個自由度,。主要結(jié)構(gòu)參數(shù)：大腿長度：214 mm；小腿長度：214 mm,；腳部長度：55 mm,；大腿質(zhì)量：6.5 kg；小腿質(zhì)量：3.5 kg,；腳部質(zhì)量：2.5 kg,。仿人行走系統(tǒng)的運動過程為：上位機下達控制指令給驅(qū)動電機；驅(qū)動電機通過同步齒形帶驅(qū)動各關(guān)節(jié)轉(zhuǎn)動,，從而實現(xiàn)仿人行走系統(tǒng)的步行運動,。各關(guān)節(jié)輸出范圍如表1所示。驅(qū)動電機主要參數(shù)如表2所示,，驅(qū)動電機輸出端安裝減速比為1:50的減速器,，提高了電機的最大力矩值。

2 基于倒立擺模型的仿人機器人數(shù)學(xué)模型的建立

　　和人類步行相似,，仿人機器人的步態(tài)行走是機器人的重心由支撐腿向前運動,，擺動腿由支撐腿的后方擺到支撐腿的前方，兩條腿的交換在瞬間完成的,。在這樣的行走過程中,，將仿人機器人行走系統(tǒng)簡化為一個倒立擺模型[6]，如圖2所示,。

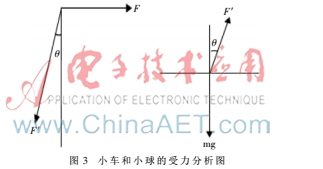
　　質(zhì)量為m的小球固結(jié)于長度為L的細桿（可忽略桿的質(zhì)量）上,，細桿又和質(zhì)量為M的小車鉸接相連。通過控制施加在小車上的力F（包括大小和方向）能夠使細桿處于θ＝0的穩(wěn)定倒立狀態(tài),。在忽略其他零件的質(zhì)量以及各種摩擦和阻尼的條件下,，推導(dǎo)小車倒立擺系統(tǒng)的數(shù)學(xué)模型。設(shè)細桿擺沿順時針方向轉(zhuǎn)動為正方向,，水平向右方向為水平方向上的正方向,。當細桿擺順時針往右運動時水平方向施加的力應(yīng)該為水平向右。

　　現(xiàn)對小車和細桿擺分別進行隔離受力分析：

　　對小車有：

　　故可得以下運動方程組：

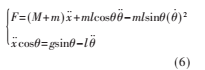
　　以上方程組為非線性方程組,，故需做如下線性化處理：

　　故空間狀態(tài)方程如下：

　　用MATLAB將狀態(tài)方程轉(zhuǎn)化成傳遞函數(shù),，取M=2 kg，m=0.1 kg，l=0.5 m代入,，可以得出角度對力F的傳遞函數(shù)為：

　　位移X對外力F的傳遞函數(shù)為：

3 仿人機器人步態(tài)行走控制器的設(shè)計

　　3.1 PID控制器的設(shè)計

　　由上節(jié)對倒立擺模型的描述,，仿人機器人的步態(tài)行走要求它的姿態(tài)角達到一個期望值，當仿人機器人受到干擾離開期望值時,，如果姿態(tài)角不能及時恢復(fù),，仿人機器人姿態(tài)失衡，最終會導(dǎo)致機器人行走失敗,。為了使仿人機器人姿態(tài)角穩(wěn)定在期望值,，保持仿人機器人姿態(tài)平衡，實現(xiàn)仿人機器人穩(wěn)定行走的目的,，本文采用以仿人機器人姿態(tài)角和位移實現(xiàn)雙閉環(huán)的PID控制算法[7-8],，干預(yù)姿態(tài)角和位移的變化，使其始終保持在穩(wěn)定狀態(tài),，從而實現(xiàn)仿人機器人的穩(wěn)定步態(tài)行走,。

　　PID控制器是一種線性控制器，它將給定值r(t)與實際輸出值c(r)的偏差的比例(P),、積分(I)、微分(D)通過線性組合構(gòu)成控制量,，對控制對象進行控制,。是一種應(yīng)用較為廣泛的控制算法，其控制性能優(yōu)越,，結(jié)構(gòu)簡單,，方便調(diào)節(jié)[9]。PID調(diào)節(jié)器各校正環(huán)節(jié)的主要作用有：

　　(1)比例環(huán)節(jié)：偏差一旦產(chǎn)生,，調(diào)節(jié)器立即產(chǎn)生控制作用以減小偏差即時成比例地反應(yīng)控制系統(tǒng)的偏差信號e(t),。

　　(2)積分環(huán)節(jié)：主要用于消除靜差，積分作用的強弱取決于積分時間常數(shù),，進提高系統(tǒng)的無差度,。

　　(3)微分環(huán)節(jié)：能反應(yīng)偏差信號的變化趨勢(變化速率)，相當于引入一個有效的早期修正信號,，從而加快系統(tǒng)的動作速度,，減小調(diào)節(jié)時間。

　　首先,，建立PID控制器的微分方程為：

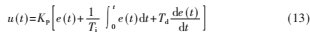
　　式中,，e(t)=r(t)-c(t)。

　　再得到PID控制器的傳遞函數(shù)為：

　　3.2 PID控制器參數(shù)調(diào)節(jié)

　　在MATLAB/Simulink中建立仿人機器人模型,，同時采用試湊法對PID參數(shù)進行調(diào)節(jié)[10],。首先，建立沒校正之前的θ-F單閉環(huán)控制系統(tǒng)，由于未加進控制環(huán)節(jié),，故系統(tǒng)輸出極易發(fā)散,。給系統(tǒng)加入PID控制環(huán)節(jié)，如圖4所示,。

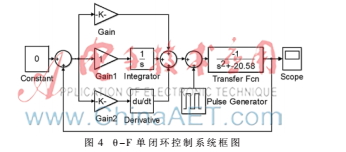
　　設(shè)置系統(tǒng)穩(wěn)定值為0,，給系統(tǒng)一個初始干擾沖擊信號，采用試湊法不斷調(diào)整PID參數(shù),，當系統(tǒng)在時域內(nèi)達到穩(wěn)定后,，進行離散化分析，建立離散模型系統(tǒng)控制框圖如圖5所示,。

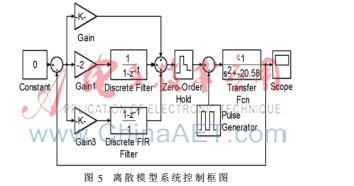
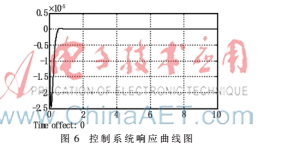
　　如圖6所示,，經(jīng)調(diào)節(jié)后，當Kp=-110,，Ti=-4,，Td=-1 500，系統(tǒng)響應(yīng)穩(wěn)定,，超調(diào)<0.3%,，調(diào)節(jié)時間<0.2 s。至此,，離散域的控制參數(shù)調(diào)節(jié)順利實現(xiàn),。圖7為建立的仿人機器人雙閉環(huán)控制系統(tǒng)。

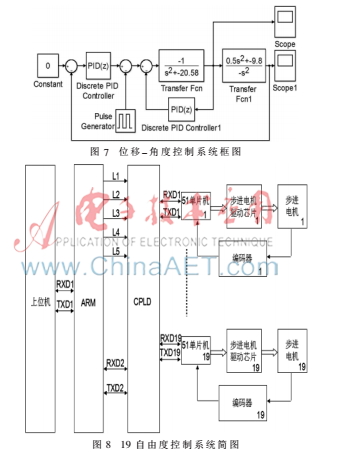
4 仿人機器人步態(tài)實驗

　　4.1 仿人行走系統(tǒng)控制系統(tǒng)硬件

　　仿人機器人運動控制器在增加了CPLD芯片后,，控制系統(tǒng)如圖8所示,。實驗?zāi)康氖球炞C本文所提PID控制器的合理性及準確性，該仿人機器人下肢有10個自由度,，上肢有9個自由度,，以STM32+CPLD為核心的控制系統(tǒng)總體方案，單一的關(guān)節(jié)控制可以使用一個51單片機芯片最小控制系統(tǒng),，控制步進電機運動[11],。

　　4.2 數(shù)值對比結(jié)果分析

　　調(diào)節(jié)行走系統(tǒng)原理樣機末端執(zhí)行器位姿為給定位姿。通過編碼器和傾角傳感器測得行走系統(tǒng)各關(guān)節(jié)輸出,。比較數(shù)據(jù)值,，如表 3所示。

　　通過驗證數(shù)值對比結(jié)果得出,，關(guān)節(jié)輸出最大相對誤差為2.25 %,，表明了本文采用仿人機器人步態(tài)行走系統(tǒng)PID控制算法的正確性及高精確度。

5 結(jié)論

　　本文針對仿人機器人步態(tài)行走不穩(wěn)定的問題,，以倒立擺為控制對象,，建立仿人機器人步態(tài)行走數(shù)學(xué)模型,。在建立數(shù)學(xué)模型時，首先用牛頓-歐拉方法建立數(shù)學(xué)模型,，而后用動態(tài)系統(tǒng)空間狀態(tài)方程法導(dǎo)出狀態(tài)方程系數(shù)矩陣,，然后用MATLAB對數(shù)學(xué)模型進行從狀態(tài)空間到傳遞函數(shù)的變換（包括傳遞函數(shù)的拉氏變換與Z變換），得到系統(tǒng)的傳遞函數(shù)模型,。最后建立仿人機器人姿態(tài)角和位移的雙閉環(huán)控制系統(tǒng),，采用PID控制算法對仿人機器人姿態(tài)角和位移進行調(diào)節(jié)。系統(tǒng)響應(yīng)穩(wěn)定,，超調(diào)量<0.3%,，調(diào)節(jié)時間<0.2 s，得到滿意的控制效果,。以19自由度仿人機器人進行實驗驗證,，其關(guān)節(jié)的輸出相對誤差最大為2.25%，可實現(xiàn)仿人機器人穩(wěn)定的步態(tài)行走,，表明了本文采用仿人機器人步態(tài)行走系統(tǒng)PID控制算法的正確性及高精確度,。

　　參考文獻

　　[1] 畢盛，閔華清,，陳強.仿人機器人步態(tài)規(guī)劃反饋控制研究綜述[J].計算機工程與應(yīng)用,，2011(7)：30-33.

　　[2] 付根平，楊宜民,，李靜.仿人機器人的步行控制方法綜述及展望[J].機床與液壓,，2011(23)：154-159.

　　[3] Tang Zhe，ER M J.Humanoid 3D gait generationbased oninverted pendulum model[C].22nd IEEE International Sym-posium on Intelligent Control Part of IEEE Multi-conferenceon Systems and Control,，2007.

　　[4] 畢盛,，閔華清,，陳強,，等.一種仿人機器人斜坡運動步態(tài)規(guī)劃方法[J].華南理工大學(xué)學(xué)報(自然科學(xué)版)，2010(11)：148-154,，160.

　　[5] 李龍澍,，王唯翔，王凡.基于三維線性倒立擺的雙足機器人步態(tài)規(guī)劃[J].計算機技術(shù)與發(fā)展,，2011(6)：66-69.

　　[6] 黎君,，閻世梁.一級倒立擺模糊PID控制器設(shè)計[J].國外電子測量技術(shù)，2012(4)：50-52.

　　[7] 郭宏,，吳海洋,，巫佩軍.基于變系數(shù)PID的無刷直流電動機雙閉環(huán)系統(tǒng)[J].北京航空航天大學(xué)學(xué)報，2012(1)：1-5.

　　[8] 王啟源,，阮曉鋼.獨輪自平衡機器人雙閉環(huán)非線性PID控制[J].控制與決策,，2012(4)：593-597.

　　[9] 劉慧博,，王靜，吳彥合.無刷直流電機模糊自適應(yīng)PID控制研究與仿真[J].控制工程,，2014(4)：583-587.

　　[10] 張斌,，姚有峰.基于串行總線下最小控制系統(tǒng)實現(xiàn)方式的研究[J].現(xiàn)代電子技術(shù)，2009(11)：149-151.

　　[11] 袁安富,，徐金琦,，王偉，等.基于雙STM32多旋翼無人機控制系統(tǒng)設(shè)計[J].電子技術(shù)應(yīng)用,，2013,，39(11)：136-138.