程功,，任正云

　　（東華大學(xué) 信息科學(xué)與技術(shù)學(xué)院,，上海 201620）

       摘要：非最小相位是指具有右半平面零,、極點(diǎn)或滯后的線性對(duì)象，在DCDC變換器中,Boost變換器以電容電壓作為輸出量進(jìn)行反饋控制時(shí),，是一個(gè)非最小相位系統(tǒng),。由于目前大多數(shù)Boost電路的控制方法選用的是傳統(tǒng)PID控制，這種方法具有結(jié)構(gòu)簡單,、可靠性高等特點(diǎn),，但是系統(tǒng)的動(dòng)態(tài)特性、抗干擾性能卻有待進(jìn)一步提高,。由于預(yù)測PI控制算法具有抗滯后和抗非最小相位特性的能力,，將其應(yīng)用到Boost電路中進(jìn)行理論研究并進(jìn)行實(shí)時(shí)仿真。仿真結(jié)果表明,，預(yù)測PI控制算法具有良好的動(dòng)態(tài)特性且抗干擾性強(qiáng),能夠體現(xiàn)良好的控制效果,。

　　關(guān)鍵詞：非最小相位；預(yù)測PI控制算法,；Boost電路

　　中圖分類號(hào)：TM919;TP271文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2017.01.002

　　引用格式：程功,，任正云. 基于Boost電路的預(yù)測PI控制［J］.微型機(jī)與應(yīng)用，2017,36（1）：4-7.

0引言

　　由于電力電子技術(shù)發(fā)展迅速,，帶動(dòng)了新能源技術(shù)的發(fā)展,，同時(shí)使功率電源得到廣泛運(yùn)用。現(xiàn)在電力電子技術(shù)常用的是開關(guān)電源技術(shù),其核心是DCDC變換器,。由于DCDC變換器具有非線性特點(diǎn),使其難以建立準(zhǔn)確的模型,。對(duì)于DCDC變換器,，傳統(tǒng)的建模方法是建立小信號(hào)模型。而實(shí)際中的過程對(duì)象大都具有非線性,、時(shí)變特征,，若采用傳統(tǒng)PID控制DCDC變換器，則會(huì)存在輸出電壓不穩(wěn),、精度低,、可調(diào)范圍小、紋波電流過大等問題［1］,。

　　本文主要研究了Boost升壓電路在預(yù)測PI控制算法和傳統(tǒng)PID控制下的動(dòng)態(tài)響應(yīng)特性,。由于Boost升壓電路是典型的DCDC功率變換器，因而是一個(gè)非最小相位系統(tǒng),，表現(xiàn)為小信號(hào)數(shù)學(xué)模型中存在右半平面的一個(gè)零點(diǎn),，這個(gè)零點(diǎn)的一個(gè)顯著特征就是在占空比突變的情況下，除發(fā)生超調(diào)外,，輸出電壓的開始階段會(huì)出現(xiàn)先下降后上升的變化,，即出現(xiàn)負(fù)調(diào)現(xiàn)象。這種負(fù)調(diào)現(xiàn)象會(huì)惡化控制系統(tǒng)的動(dòng)態(tài)品質(zhì),，導(dǎo)致系統(tǒng)的過渡時(shí)間延長,，因此對(duì)Boost電路而言抑制負(fù)調(diào)非常重要［2］。

　　針對(duì)上述Boost升壓電路的非線性特征,，本文采用預(yù)測PI控制算法對(duì)Boost升壓電路進(jìn)行控制,，使其具有良好的控制效果。實(shí)際仿真表明,預(yù)測PI控制算法具有很好的動(dòng)態(tài)控制特性和抗干擾性,。

1Boost變換器

　　圖1Boost變換器電路結(jié)構(gòu)Boost升壓電路采用閉環(huán)回路控制,，采用傳統(tǒng)PID進(jìn)行控制，就必需對(duì)系統(tǒng)建立一個(gè)比較準(zhǔn)確的數(shù)學(xué)模型,。而在電力電子技術(shù)中,，常用的方法是建立小信號(hào)模型，然后根據(jù)系統(tǒng)的幅頻特性對(duì)其進(jìn)行補(bǔ)償,，最后計(jì)算得到PID控制器參數(shù),。對(duì)Boost電路建立小信號(hào)模型時(shí)，通過忽略開關(guān)頻率諧波等因素來簡化模型,，所以在研究某一穩(wěn)定工作點(diǎn)附近的動(dòng)態(tài)特性時(shí),，需要將其近似為線性系統(tǒng)［3］。Boost電路原理圖如圖1所示,。

　　由小信號(hào)模型可以用下式得占空比D:

　　如果要求電壓輸入為12 V,，電流輸出為5 A，電壓輸出為18 V，開關(guān)頻率為50 kHz,，紋波電壓小于0.1 V,，則通過式(1)~式(4)并且微調(diào)電感、電容參數(shù),，分別取電感L=1 mH,電容C=0.000 4 F,，可推出在小信號(hào)模型下的Boost電路的傳遞函數(shù)模型為：

　　其中得出:

　　kp=3×107,Tp=6.225×10－4

　　其中kp代表控制過程的開環(huán)增益，Tp表示過程的時(shí)間常數(shù),。由此可推出該傳遞函數(shù)是一個(gè)非最小相位系統(tǒng)的傳遞函數(shù),，其開環(huán)階躍響應(yīng)如下圖2所示。

　　由圖2可以得出,，曲線在初始時(shí)有明顯的負(fù)調(diào)現(xiàn)象,。電感L、電容C共同決定系統(tǒng)啟動(dòng)時(shí)的超調(diào)量和上升時(shí)間,，而此時(shí)的傳遞函數(shù)表明該系統(tǒng)有一個(gè)右半平面的零點(diǎn),，這個(gè)零點(diǎn)位置會(huì)隨Boost變換器的電感、電容變化而變化,，這種現(xiàn)象會(huì)惡化控制系統(tǒng)的動(dòng)態(tài)品質(zhì),，導(dǎo)致系統(tǒng)的過渡時(shí)間變長，而且在負(fù)調(diào)時(shí)間段內(nèi),，控制器接受到相反的反饋信號(hào),，形成正反饋系統(tǒng)，嚴(yán)重影響系統(tǒng)的穩(wěn)態(tài)性能［4］,。對(duì)此傳遞函數(shù)進(jìn)行一階Pade近似，即：

　　其中τ為延遲環(huán)節(jié),，此時(shí)如果給式(6)配置式（7）,，進(jìn)行一階Pade近似會(huì)使負(fù)調(diào)現(xiàn)象在仿真中消失,從而擬合成一個(gè)消除負(fù)調(diào)現(xiàn)象的滯后系統(tǒng)，即：

　　從式(9)中可以得出,，含有延遲環(huán)節(jié)的非最小相位系統(tǒng)是含有右半復(fù)平面零點(diǎn)非最小相位系統(tǒng)的一種特殊情況［5］,。

2系統(tǒng)辨識(shí)擬合

　　傳遞函數(shù)的辨識(shí)時(shí)域方法包括階躍響應(yīng)法、脈沖響應(yīng)法等,，其中以階躍響應(yīng)法最為常用［45］,。通過對(duì)上述圖形分析，進(jìn)一步對(duì)其進(jìn)行系統(tǒng)辨識(shí)擬合,，采用二階欠阻尼自衡對(duì)象的辨識(shí),。對(duì)于傳遞函數(shù)：

　　式中，w0為自然頻率,，ξ為阻尼系數(shù),，當(dāng)ξ<1時(shí)，稱為欠阻尼系數(shù)。

　　在階躍輸入激勵(lì)下,，系統(tǒng)輸出會(huì)出現(xiàn)震蕩現(xiàn)象,，采用拉式變換，得出無因次曲線為：

　　由二階欠阻尼自衡對(duì)象的擬合辨識(shí)方法得出t1=0.003 7 s和t2=0.01 s時(shí)刻的值分別為Y1=38.7 V,，Y2=28.5 V,。

　　由公式:

　　得到K=27.270,用階躍響應(yīng)對(duì)其仿真，如圖3所示,。

　　接著繼續(xù)對(duì)此傳遞函數(shù)進(jìn)行一階慣性對(duì)象的傳遞函數(shù)擬合,，傳遞函數(shù)擬合一般有兩種經(jīng)典方法：切線法和計(jì)算法。下面通過計(jì)算法來辨識(shí)出需要的傳遞函數(shù),。

　　根據(jù)公式：

　　取t1=0.004 5 s,y1*=1.432,t2=0.011 s,y2*=1.08,帶入式(14),、(15)，得到τ=0.001 868 s,，T=0.000 324,。即一階慣性滯后的擬合傳遞函數(shù)如下：

　　3預(yù)測PI控制算法

　　傳統(tǒng)的PID控制算法在控制器參數(shù)整定時(shí)比較麻煩，整定參數(shù)較多,。自1992年Hagglund提出預(yù)測PI控制器的思想,，預(yù)測PID算法得到了逐步的發(fā)展和完善，形成了預(yù)測算法和PID算法融合在一起的控制器,。這種控制器中,，包括預(yù)測控制器和PID 控制器，PID控制器與過程的滯后時(shí)間無關(guān),，根據(jù)以前的控制作用給出現(xiàn)在的控制作用,。這種控制器已經(jīng)成功應(yīng)用于實(shí)際的工業(yè)過程。預(yù)測PI控制器由兩部分組成：PI部分和預(yù)測部分,，總共有5個(gè)參數(shù),，其中3個(gè)為可調(diào)參數(shù)［67］。其結(jié)構(gòu)圖如圖4所示,。

　　假設(shè)控制對(duì)象傳遞函數(shù)為：

　　上式右邊第一項(xiàng)具有PI控制器的結(jié)構(gòu)形式,能夠提高控制器的穩(wěn)定性, 在不同干擾存在和模型發(fā)生變化時(shí), 都能保持良好的控制性能,。第二項(xiàng)可以解釋為：控制器在t時(shí)刻的輸出是基于時(shí)間區(qū)間［t-τ,t］上的輸出預(yù)測而得到的［8］。這種控制器稱為預(yù)測PI控制器(PPI),。引入預(yù)測控制項(xiàng)是為了克服純滯后對(duì)控制的不利影響,。在預(yù)測PI控制器參數(shù)選取上，kp一般選為過程增益的倒數(shù),，T為過程達(dá)到穩(wěn)態(tài)值的時(shí)間常數(shù),，τ為過程的滯后時(shí)間。其中λ是可調(diào)參數(shù),，當(dāng)λ=1時(shí),，系統(tǒng)的開環(huán)與閉環(huán)的響應(yīng)時(shí)間常數(shù)一致,；當(dāng)λ>1時(shí)，系統(tǒng)的閉環(huán)響應(yīng)比開環(huán)響應(yīng)要慢,；當(dāng)λ<1時(shí),，系統(tǒng)的閉環(huán)響應(yīng)比開環(huán)響應(yīng)要快［9］。圖4中的Gc1(s)和Gc2(s)分別為：

　　E(s),、U(s)分別為控制器的輸入和輸出,。由結(jié)構(gòu)可知預(yù)測PI控制算法同時(shí)具有PI算法的功能和預(yù)測功能，對(duì)帶有滯后對(duì)象的系統(tǒng)能夠進(jìn)行有效控制,，而且控制簡單,，參數(shù)調(diào)節(jié)方便［10-11］。

4Boost電路的預(yù)測PI控制仿真及結(jié)果分析

　　利用預(yù)測PI控制算法對(duì)Boost電路進(jìn)行控制,，其控制原理如圖5所示,。

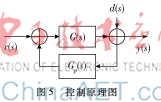
　　其中G(s)為Boost電路的傳遞函數(shù)，Gp(s)為預(yù)測PI控制器,，d(s)為擾動(dòng)項(xiàng),，且由式可知，G(s)傳遞函數(shù)為：

　　基于MATLAB中的Simulink工具包中的仿真工具,，模擬構(gòu)造控制系統(tǒng),，通過對(duì)系統(tǒng)的仿真，可以實(shí)時(shí)觀測控制系統(tǒng)的動(dòng)態(tài)特性,，并對(duì)控制方案進(jìn)行分析,。首先采用傳統(tǒng)PID控制方法對(duì)Boost電路進(jìn)行仿真，得到仿真圖如圖6,。

　　為了檢驗(yàn)預(yù)測PI控制算法在Boost電路中的性能,，將其與傳統(tǒng)PID控制算法進(jìn)行仿真比較。如圖7,。

　　對(duì)比可得,，預(yù)測PI控制算法比傳統(tǒng)PID算法在面對(duì)非最小相位系統(tǒng)對(duì)象時(shí)，穩(wěn)定性和快速性具有良好的效果,，同時(shí)震蕩幅度也比傳統(tǒng)PID要優(yōu)良，并且大幅度縮短了系統(tǒng)響應(yīng)時(shí)間,，提高了系統(tǒng)快速性,。

　　當(dāng)系統(tǒng)達(dá)到穩(wěn)態(tài)后，如果隨機(jī)給穩(wěn)態(tài)系統(tǒng)加上擾動(dòng),，例如在0.3 s時(shí)加上一個(gè)擾動(dòng)項(xiàng),，即加上一個(gè)3 V的階躍信號(hào)充當(dāng)干擾量，以及同樣在0.3 s時(shí)加另外一個(gè)階躍信號(hào)幅值為-3 V的擾動(dòng)項(xiàng),，觀察此時(shí)的預(yù)測PI控制以及傳統(tǒng)PID控制下的Boost電路的波形圖,。仿真結(jié)果如圖8、圖9所示。

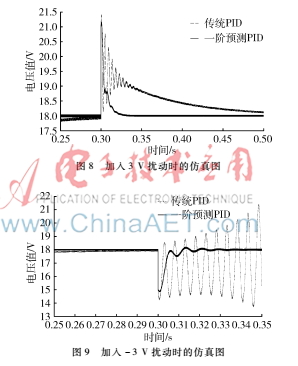
　　通過觀察上述兩圖,，Boost電路在預(yù)測PI控制算法下,，能夠快速穩(wěn)定地達(dá)到穩(wěn)態(tài)值，同時(shí)超調(diào)量小,，動(dòng)態(tài)響應(yīng)優(yōu)越,，而傳統(tǒng)PID算法下的Boost電路，在加上-3 V的擾動(dòng)項(xiàng)下,，會(huì)出現(xiàn)發(fā)散,，不能夠達(dá)到穩(wěn)態(tài)，動(dòng)態(tài)響應(yīng)差,，從而證明了基于一階預(yù)測PI的Boost電路的抗干擾性能和魯棒性比傳統(tǒng)PID優(yōu)越,。5結(jié)論

　　本文針對(duì)DCDC功率變換器中的典型Boost電路的非最小相位行為，提出了基于預(yù)測PI的控制算法,，并在理論上進(jìn)行了研究與分析,。仿真結(jié)果顯示被控系統(tǒng)具有良好的響應(yīng)曲線，并與傳統(tǒng)的PID控制器進(jìn)行了仿真對(duì)比,，通過兩者的響應(yīng)曲線,，表明了預(yù)測PI控制器可以實(shí)現(xiàn)高精度、強(qiáng)魯棒性,、快速性的性能,，從而避免了傳統(tǒng)PID在系統(tǒng)過程中出現(xiàn)的高超調(diào)、震蕩大,、響應(yīng)慢,、穩(wěn)定性差等缺點(diǎn)，說明了預(yù)測PI控制算法比傳統(tǒng)PID在性能上增強(qiáng)了系統(tǒng)的抗干擾能力,，改善了控制性能,，而且在參數(shù)整定方法上比較容易獲得。因此基于預(yù)測PI算法的Boost電路是一種優(yōu)良的控制方案,。而且文中提出的預(yù)測PI控制器可以同時(shí)用在Buck電路和BuckBoost電路中,，是一種新的實(shí)用控制方式。

　　參考文獻(xiàn)

　?。?］ 王淯舒,孫培德,呂蕾.基于自整定模糊PID控制的Buck變換器設(shè)計(jì)與仿真［J］.自動(dòng)化與信息工程,2014, 35(5):39 45.

　?。?］ 馬增輝,劉長良.一類非最小相位系統(tǒng)的PID控制器整定方法［J］.信息與控制,2015,44(2):147 151.

　　［3］ 李鵬波,，胡德文,，張紀(jì)陽．系統(tǒng)辨識(shí)［M］．北京：中國水利水電出版社，2010．

　?。?］ 皇金鋒,劉樹林.Boost變換器的參數(shù)選擇與非最小相位分析［J］.電機(jī)與控制學(xué)報(bào),2014,18(7):51 59.

　?。?］ 徐德鴻.電力電子系統(tǒng)建模及控制［M］．北京：機(jī)械工業(yè)出版社,，2005．

　　［6］ 任正云.預(yù)測PID控制及其在工業(yè)中的應(yīng)用［D］. 上海：上海交通大學(xué),2003．

　?。?］ SCHEI T S. A method for closed loop automatic tuning of PID controllers［J］. Automatica, 1992, 28(3): 587 591.

　?。?］ RAD A B.Predictive PI controller［J］.International Journal of Control,2007,60(5):953 957.

　　［9］ 任正云,，邵惠鶴,，張立群. 幾種特殊動(dòng)態(tài)特性對(duì)象的預(yù)測PI控制［J］.儀器儀表學(xué)報(bào),2004,25(5):617618.

　　［10］ ZHENG D, REN Z Y, FANG J A. Stability analysis of multiple timedelayed system［J］.ISA Transactions,2008, 47(3): 439 447.

　?。?1］ AIRIKKA P.Stability analysis of a predictive PI controller［C］. Control & Automation (MED), 2013 21st Mediterranean Conference on. IEEE, 2013: 1380 1385.