張昊,，葉宇煌

　?。ǜＶ荽髮W(xué) 物理與信息工程學(xué)院，福建 福州 350116）

       摘要：測斜儀在石油勘探,、地質(zhì)勘查等方面已成為一種有力的工具,，但基于磁通門的測斜儀存在著易受磁場干擾的缺點(diǎn)，導(dǎo)致其測量精度降低,，甚至無法工作,。為了解決這一問題,，提出了一種基于捷聯(lián)慣性導(dǎo)航原理的連續(xù)測斜算法。算法利用微慣性傳感器MPU6050獲取姿態(tài)數(shù)據(jù),，采用四元數(shù)方法進(jìn)行姿態(tài)解算,，最終得到鉆探過程中的傾斜角、方位角以及工具面角等數(shù)據(jù),。通過仿真驗(yàn)證,，得到測量誤差曲線。仿真結(jié)果表明,，該算法可以實(shí)現(xiàn)全方位井眼軌跡連續(xù)測量,，提高了測量效率。

　　關(guān)鍵詞：測斜儀,；捷聯(lián)慣性導(dǎo)航,；四元數(shù)；姿態(tài)解算

　　中圖分類號(hào)：TP391.9文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2017.01.005

　　引用格式：張昊,，葉宇煌. 基于微慣性傳感器的測斜儀姿態(tài)算法的研究［J］.微型機(jī)與應(yīng)用,，2017,36（1）：15-17.

0引言

　　隨著科學(xué)技術(shù)的發(fā)展，煤炭開采范圍也越來越大,，復(fù)雜的地質(zhì)環(huán)境使得安全生產(chǎn)問題日益嚴(yán)重,。查明工作面的地質(zhì)構(gòu)造以及精確的工程鉆探，都需要精度高,、穩(wěn)定性好且能全方位測量鉆孔軌跡的測斜儀,。目前存在的測斜儀主要有兩類：一類是基于磁通門的測斜儀，但這種測斜儀在鐵礦豐富的地區(qū)會(huì)受到極大的干擾,，以至于無法工作,；第二類采用機(jī)械式陀螺作為測量單元，雖然不受周圍環(huán)境的影響,，但它只能進(jìn)行靜態(tài)單點(diǎn)測量,，測量時(shí)間長［13］。

　　本文將捷聯(lián)慣性導(dǎo)航應(yīng)用在測斜儀中,，利用測斜儀中的三軸陀螺儀和三軸加速度微慣性傳感器測得姿態(tài)數(shù)據(jù),，輸出的數(shù)據(jù)經(jīng)過姿態(tài)解算，可直接輸出測斜儀的三個(gè)姿態(tài)角信息,。捷聯(lián)慣性導(dǎo)航直接將慣性器件捆綁在載體之上,，不依賴于外界信息，因此具有結(jié)構(gòu)簡單,、體積小,、成本低、可靠性高等優(yōu)點(diǎn)［4］,。

1捷聯(lián)慣性導(dǎo)航原理

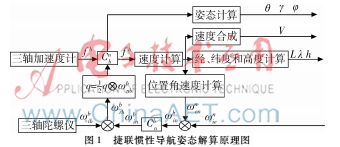
　　由于慣性傳感器是與載體捆綁在一起的,，因此與載體一起運(yùn)動(dòng)，陀螺儀測得的角速度和加速度計(jì)測得的比力都是在載體坐標(biāo)系當(dāng)中的,，因此只有將其中的角速度和比力信息轉(zhuǎn)換到導(dǎo)航坐標(biāo)系中,，才能夠?qū)崿F(xiàn)對(duì)載體姿態(tài)的解算［5］，基本原理如圖1所示,。所以姿態(tài)解算算法是捷聯(lián)慣性導(dǎo)航的關(guān)鍵技術(shù),，解算算法的好壞直接影響導(dǎo)航系統(tǒng)的精度。常見的姿態(tài)解算方法有以下4種［6］：

　?。?）歐拉角法,，當(dāng)俯仰角為90°時(shí)，歐拉微分方程存在著退化問題,，不能全姿態(tài)工作,，只適合應(yīng)用在水平姿態(tài)變化不大的載體上。

　?。?）方向余弦法可以全姿態(tài)工作,，但是需要解算9個(gè)微分方程，計(jì)算復(fù)雜,。

　?。?）四元數(shù)算法只需要求解4個(gè)微分方程，計(jì)算簡便,，但引入不可交換性誤差,，一般不適合于激烈運(yùn)動(dòng)的運(yùn)動(dòng)載體的姿態(tài)解算。

　?。?）等效旋轉(zhuǎn)矢量法,，通過多子樣算法彌補(bǔ)了四元數(shù)算法存在的不可交換性誤差的缺點(diǎn)，適用于高動(dòng)態(tài)運(yùn)動(dòng)載體的姿態(tài)解算,。子樣數(shù)越多,，姿態(tài)解算的精度也就越高，同時(shí)計(jì)算復(fù)雜度也隨之增加,。相比于四元數(shù)法的計(jì)算量增加了30%,。

　　四元數(shù)法和等效旋轉(zhuǎn)矢量法都能夠全姿態(tài)工作且精度高，所以在工程中經(jīng)常用到,。雖然四元數(shù)法相對(duì)于等效旋轉(zhuǎn)矢量法存在不可交換性誤差,，不能在激烈運(yùn)動(dòng)的載體上應(yīng)用，但可以應(yīng)用到低速運(yùn)動(dòng)的測斜儀中,。

　　1.1坐標(biāo)系定義

　　慣性坐標(biāo)系記為i,，原點(diǎn)位于地心，xi指向春分點(diǎn),，zi沿地球自轉(zhuǎn)軸,，yi與xi,、zi軸構(gòu)成右手系。選取地理坐標(biāo)系作為導(dǎo)航坐標(biāo)系,，記為n系,，原點(diǎn)位于載體質(zhì)心，zn分別指向所在地的東,、北,、天。載體坐標(biāo)系記為b系,，xb,、yb、zb分別指向右,、前,、上。

　　1.2坐標(biāo)變換

　　兩坐標(biāo)系間任何復(fù)雜的角位置關(guān)系都可以看作有限次基本旋轉(zhuǎn)的復(fù)合,，變換矩陣等于基本旋轉(zhuǎn)確定的變換矩陣的連乘,，連乘順序依基本旋轉(zhuǎn)的先后次序由右向左排列。所以載體坐標(biāo)系與導(dǎo)航坐標(biāo)系之間的轉(zhuǎn)換可以用下面的矩陣表示：

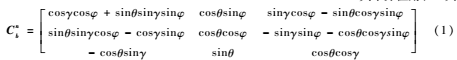　　其中φ為方位角（航向角）,，θ為井斜角（俯仰角）,，γ為工具面角（橫滾角），Cnb稱為載體的姿態(tài)矩陣,。式中Cnb與旋轉(zhuǎn)次序有關(guān),，即當(dāng)旋轉(zhuǎn)角φ、θ,、γ不都為小角時(shí),，對(duì)應(yīng)于不同的旋轉(zhuǎn)次序，坐標(biāo)系n的最終空間位置是不同的,，這就是常說的有限轉(zhuǎn)動(dòng)的不可交換性,。但當(dāng)φ、θ,、γ都為小角時(shí),，忽略小角間的高階小量,式（1）變?yōu)椋?/p>

　　式中，φ,、θ,、γ的單位為弧度。此時(shí)由φ,、θ,、γ構(gòu)成的列向量［φθγ］T可視為三維空間矢量，各分量正負(fù)號(hào)的規(guī)定為：當(dāng)產(chǎn)生小角的旋轉(zhuǎn)方向與坐標(biāo)軸指向相同時(shí)該小角取正，否則取負(fù),。此時(shí)旋轉(zhuǎn)后坐標(biāo)系的最終角位置與旋轉(zhuǎn)次序無關(guān),，這就是常說的無限轉(zhuǎn)動(dòng)與次序無關(guān)［7］。由于直角坐標(biāo)系之間的變換矩陣為單位正交矩陣,，所以如果在坐標(biāo)系b至坐標(biāo)系n的等效旋轉(zhuǎn)中各坐標(biāo)系都保持為直角坐標(biāo)系,，則根據(jù)正交單位矩陣的性質(zhì)有［8］：

　　Cnb=(Cbn)－1=(Cbn)T（3）

　　2四元數(shù)算法

　　四元數(shù)是由4個(gè)元構(gòu)成的數(shù)：

　　q=q1+q2i+q3j+q4k（4）

　　式中，q1,、q2、q3,、q4是實(shí)數(shù),，i、j,、k是相互正交的單位向量,，又是虛單位－1。根據(jù)歐拉定理,，空間中兩坐標(biāo)系的相對(duì)位置,，可以等效為動(dòng)坐標(biāo)系繞某一瞬軸u（單位向量）轉(zhuǎn)過角θ一次完成。u和θ可以用來表示一個(gè)四元數(shù)：

　　2.1四元數(shù)表示的姿態(tài)矩陣

　　式（5）描述了剛體的定點(diǎn)轉(zhuǎn)動(dòng),，即當(dāng)只關(guān)心b系相對(duì)于n系的角位置時(shí),，可認(rèn)為b系是由n系經(jīng)過無中間過程的一次性等效旋轉(zhuǎn)形成的，q包含了這種等效旋轉(zhuǎn)的全部信息：u為旋轉(zhuǎn)瞬軸和旋轉(zhuǎn)方向,，θ為轉(zhuǎn)過的角度,。因此可以確定出b系至n系的坐標(biāo)變換矩陣為：

　　由式（1）與式（6）可以得出:

　　θ主=arcsin(T32)

　　γ主=arctan(－T31/T33)

　　φ主=arctan(T12/T22)（7）

　　其中方位角和工具面角的真值可以按照表1和表2進(jìn)行確定。

　　2.2四元數(shù)的微分方程及求解

　　四元數(shù)的姿態(tài)更新微分方程表示如下：表1方位角的真值T11T21φ0+90°0-－90°++φ主-φ主-+φ主+180°--φ主－180°表2工具面角的真值T33γ主γ++-γ主-+γ主－180°--γ主+180°dqdt=12qωbnb（8）

　　式中ωbnb=ωxωyωzT,。寫成矩陣形式：

　　其中,，ωbnb可由下式計(jì)算得到：

　　ωbnb=ωbib－Cbn(ωnie+ωnen)（11）

　　式中，ωbib為三軸陀螺儀的輸出,，表示載體坐標(biāo)系相對(duì)于慣性坐標(biāo)系的角速度,； ωnie表示地球坐標(biāo)系相對(duì)于慣性坐標(biāo)系e在載體坐標(biāo)系中的角速度；ωnen表示導(dǎo)航坐標(biāo)系相對(duì)于慣性坐標(biāo)系在導(dǎo)航坐標(biāo)系下的角速度,。

　　利用畢卡求解法對(duì)式（10）進(jìn)行解算得：

　　3驗(yàn)證

　　利用MATLAB軟件對(duì)以上算法進(jìn)行仿真驗(yàn)證,。設(shè)計(jì)的方位角、井斜角和工具面角的變化規(guī)律如圖2所示,，初始方位角為68.9°,，初始井斜角為0°，初始工具面角為178°,；采樣頻率為100 Hz,。由于加入儀器誤差后使得誤差來源不明，所以本次仿真實(shí)驗(yàn)?zāi)J(rèn)慣性傳感器的輸出為理想狀態(tài)下的輸出,。通過本文設(shè)計(jì)的算法對(duì)傳感器的輸出進(jìn)行解算,，最終結(jié)果如圖3所示,。　　

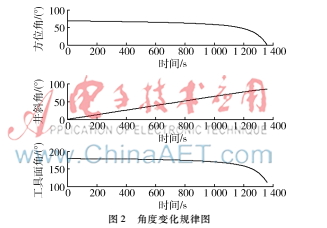
　　由圖3可以看出方位角的理論解算誤差控制在±1°以內(nèi),，井斜角誤差控制在±0.1°以內(nèi),，工具面角誤差控制在±1°以內(nèi)，具有良好的解算精度,，證明本文提出的解算方法有效,。

4結(jié)論

　　本文提出了一種新的基于捷聯(lián)慣性導(dǎo)航原理的連續(xù)測斜算法，并進(jìn)行了模擬仿真,。仿真結(jié)果表明該解算算法可以實(shí)現(xiàn)解算姿態(tài)的功能,，在保證測量精度的同時(shí)，比之前的靜態(tài)測量縮短了測量時(shí)間,，提高了測量的效率,。但該算法在長時(shí)間測量的情況下可能會(huì)出現(xiàn)測量精度降低的情況，這可能是因?yàn)榉e分的累計(jì)誤差造成,，有待進(jìn)一步的研究,。

參考文獻(xiàn)

　　［1］ 謝子殿, 朱秀. 基于磁通門與重力加速度傳感器的鉆井測斜儀［J］. 傳感器與微系統(tǒng), 2004, 23(7):30-33.

　?。?］ NOY K A, LEONARD J G. A new rate gyroscopicwellbore survey system achieves the accuracy and operational flexibility needed for today's complex drilling challenges［C］.SPE/IADC Drilling Conference, Society of Petroleum Engineers, 1997.

　?。?］ 劉宇, 李秋俊, 劉俊. 基于壓電陀螺的快速方位測井短接［J］. 電子測量與儀器學(xué)報(bào), 2007, 21(2):90-94.

　　［4］ 張春慧. 高精度捷聯(lián)式慣性導(dǎo)航系統(tǒng)算法研究［D］. 哈爾濱：哈爾濱工程大學(xué), 2005.

　?。?］ 丁君. 基于微慣性傳感器的姿態(tài)算法研究［D］. 上海：上海交通大學(xué), 2013.

　?。?］ 張露. 基于捷聯(lián)慣導(dǎo)的采煤機(jī)位姿解算算法研究［D］. 西安:西安科技大學(xué), 2014.

　　［7］ 秦永元. 慣性導(dǎo)航［M］. 北京：科學(xué)出版社, 2014.

　?。?］ 彭勁松. 機(jī)載激光捷聯(lián)慣導(dǎo)優(yōu)化算法研究［D］. 西安：西北工業(yè)大學(xué), 2006.