張俊俊,，何良華

　?。ㄍ瑵?jì)大學(xué) 電子與信息工程學(xué)院,，上海 201800）

        摘要：深度學(xué)習(xí)是一類新興的多層神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)算法,，因其緩解了傳統(tǒng)訓(xùn)練算法的局部最小性，故引起機(jī)器學(xué)習(xí)領(lǐng)域的廣泛關(guān)注,。但是,，如何使一個網(wǎng)絡(luò)模型在選取任意數(shù)值的隱藏層節(jié)點數(shù)時都能夠得到一個比較合適的網(wǎng)絡(luò)結(jié)構(gòu)是目前深度學(xué)習(xí)界普遍存在的一個開放性問題,。文章提出了一種能夠動態(tài)地學(xué)習(xí)模型結(jié)構(gòu)的算法——最大判別能力轉(zhuǎn)換法，根據(jù)Fisher準(zhǔn)則來評估隱藏層每一個節(jié)點的判別性能,，然后通過動態(tài)地選擇部分隱層節(jié)點來構(gòu)建最優(yōu)的模型結(jié)構(gòu),。

　　關(guān)鍵詞：深度學(xué)習(xí)；最大判別能力轉(zhuǎn)換法,；Fisher準(zhǔn)則,；深度信念網(wǎng)絡(luò)

　　中圖分類號：TP183文獻(xiàn)標(biāo)識碼：ADOI： 10.19358/j.issn.1674-7720.2017.01.018

　　引用格式：張俊俊，何良華. 動態(tài)深度信念網(wǎng)絡(luò)模型構(gòu)建［J］.微型機(jī)與應(yīng)用,，2017,36（1）：59-61,，65.

0引言

　　深度學(xué)習(xí)可以讓那些擁有多個處理層的計算模型來學(xué)習(xí)具有多層次抽象的數(shù)據(jù)的表示。這些方法在許多方面都帶來了顯著的改善,，包括最先進(jìn)的語音識別,、視覺對象識別、對象檢測和許多其他領(lǐng)域,，例如藥物發(fā)現(xiàn)和基因組學(xué)等,。

　　然而，在很多應(yīng)用問題中,，經(jīng)常會遇到很高維度的數(shù)據(jù),，高維度的數(shù)據(jù)會造成很多問題，例如導(dǎo)致算法運(yùn)行性能以及準(zhǔn)確性的降低,。特征選?。‵eature Selection）技術(shù)的目標(biāo)是找到原始數(shù)據(jù)維度中的一個有用的子集，再運(yùn)用一些有效的算法,，實現(xiàn)數(shù)據(jù)的聚類,、分類以及檢索等任務(wù)。好的特征可以提供數(shù)據(jù)的語義和結(jié)構(gòu)信息,，使簡單的模型結(jié)構(gòu)也能取得良好的學(xué)習(xí)效果,。然而，如何選取恰當(dāng)?shù)奶卣鞑@取一個準(zhǔn)確的模型結(jié)構(gòu)仍然是深度學(xué)習(xí)模型構(gòu)建的一個開放性問題,。近年來很多相關(guān)工作［12］被提出,，使得特征選取越來越多地受到關(guān)注，另外一些關(guān)于數(shù)據(jù)譜分析以及L1正則化模型的研究,，也啟發(fā)了特征選取問題一些新的工作的開展,。并且，隨著計算機(jī)與網(wǎng)絡(luò)的發(fā)展,，人們越來越多地關(guān)注大規(guī)模數(shù)據(jù)的處理問題,，使得研究與應(yīng)用能夠真正銜接在一起。傳統(tǒng)的特征選取方法普遍采用依賴于經(jīng)驗或者模型參數(shù)的調(diào)整，例如dropout［3］,、dropconnect［4］等,。這些方法都要求在模型使用的初始時結(jié)構(gòu)就必須確定下來，并在模型的整個訓(xùn)練過程中結(jié)構(gòu)都不再發(fā)生變化,。這在一定程度上限制了模型的表達(dá)能力,。

　　基于此，本文提出一種能夠動態(tài)地學(xué)習(xí)模型結(jié)構(gòu)的算法——最大判別能力轉(zhuǎn)換法,，來根據(jù)Fisher準(zhǔn)則評估隱藏層每一個節(jié)點的判別性能,，然后通過動態(tài)地選擇部分隱層節(jié)點來構(gòu)建最優(yōu)的模型結(jié)構(gòu)。其中,，對于隱藏層節(jié)點數(shù)目的選取是通過考慮模型計算復(fù)雜度以及信息保留程度權(quán)衡后的計算結(jié)果,。

1深度信念網(wǎng)絡(luò)

　　深度學(xué)習(xí)是具有多層隱藏層的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，這種網(wǎng)絡(luò)具有更好的學(xué)習(xí)特征的能力,，對原始特征具有更本質(zhì)的描述,，從而更利于可視化或分類。其中,，深度信念網(wǎng)絡(luò)［5］（Deep Belief Network, DBN）是比較具有代表性的模型之一,，也是最簡單的深度學(xué)習(xí)模型。為了有效克服深度神經(jīng)網(wǎng)絡(luò)在訓(xùn)練上的難度,，其采用了無監(jiān)督貪婪學(xué)習(xí)的逐層初始化方式（即BP算法）,。

　　深度信念網(wǎng)絡(luò)是一種生成型概率模型，是由多個限制玻爾茲曼機(jī)（Restricted Boltzmann Machine,，RBM）堆疊組成的層次結(jié)構(gòu),。

　　DBN是通過堆疊RBMs而成，如圖1所示,，使用輸入樣本觀測值作為第一層RBM的輸入,，將由輸入訓(xùn)練出的輸出作為第二層RBM的輸入，以此類推,，通過疊加RBM模型完成深度模型的構(gòu)建,。

　　RBM訓(xùn)練模式受物理學(xué)的能量模型啟發(fā)，事物在能量最低時所處的狀態(tài)是最穩(wěn)定的,，于是構(gòu)建RBM的穩(wěn)態(tài)就成了狀態(tài)優(yōu)化的問題,，這一問題可以進(jìn)一步轉(zhuǎn)化為求極值與優(yōu)化的問題。對于圖1所示的RBM模型,，假設(shè)輸入層節(jié)點為v,，隱藏層輸出節(jié)點為h，輸入輸出層之間的權(quán)重為w,，那么輸入層向量v與輸出層向量h之間的能量函數(shù)E為：

　　其中,，a、b分別為對應(yīng)可視層和隱藏層的偏移，V,、H分別表示可視層和隱藏層的節(jié)點數(shù)。那么,，由能量函數(shù)得到可視層v與隱藏層h之間聯(lián)合函數(shù)為：

　　其中尖括號的運(yùn)算表示相對于下標(biāo)的預(yù)期分布內(nèi)積,，由此，log似然函數(shù)梯度權(quán)重的更新規(guī)則如下：

　　Δwij=ε(<vihj>data-<vihj>model)(8)

　　其中ε表示學(xué)習(xí)率,。然而上式中計算后一項需要花費很多額外的時間,，為了減小這種額外花費，對比散度（Contrastive Divergence）方法被用來計算梯度,，所以新的更新規(guī)則如下：

　　Δwij=ε(<vihj>data-<vihj>recon)(9)

　　后一項表明了重構(gòu)后的可視層與隱藏層的期望值,，實踐證明該方法得到充分應(yīng)用后具有良好的特性。相比于傳統(tǒng)的Sigmod信度網(wǎng)絡(luò),，通過以上方式學(xué)習(xí)的RBM具有權(quán)值容易學(xué)習(xí)的優(yōu)點,。

　　深度學(xué)習(xí)是具有多層隱藏層的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，這種網(wǎng)絡(luò)具有更好的學(xué)習(xí)特征的能力,，對原始特征具有更本質(zhì)的描述,，從而更利于可視化或分類。為了有效克服深度神經(jīng)網(wǎng)絡(luò)在訓(xùn)練上的難度,，采用了無監(jiān)督貪婪學(xué)習(xí)的逐層初始化方式,。深度信念網(wǎng)是其中比較具有代表性的模型之一，也是最簡單的深度學(xué)習(xí)模型,。

2結(jié)構(gòu)計算

　　每一個隱藏層節(jié)點代表了映射空間中的一個維度,，將可視層映射到隱藏層的過程就類似于一種空間變換，也就是把源數(shù)據(jù)轉(zhuǎn)換到了一個更加容易區(qū)分的新的映射空間,。然而,，這種空間變換的方式，例如：PCA,、ICA,、LDA等，所產(chǎn)生的各個維度在不同的空間中有不同的判別能力,。

　　故本文基于Fisher準(zhǔn)則［6］,，評估每個節(jié)點的判別能力，然后根據(jù)最大判別能力轉(zhuǎn)換法選取部分隱藏層節(jié)點來構(gòu)成新的映射空間,，剔除冗余或者對判別能力產(chǎn)生副作用的投影維度,，來提高此投影空間判別性能。

　　2.1節(jié)點評估

　　Fisher準(zhǔn)則函數(shù)通過計算每個節(jié)點的類間與類內(nèi)的比值來確定其在此投影空間中每個維度的判別能力,。

　　定義數(shù)據(jù)集中共有N個樣本屬于C類,，每一類分別包含Nc個樣本，uc、u分別表示樣本Xc在第c類的均值以及所有樣本的均值,。第j個特征的Fisher的值表示為：

　　2.2最具判別能力轉(zhuǎn)換法

　　Fisher準(zhǔn)則僅僅能夠判別每個特征的判別性能,，卻無法計算每層隱藏層具體多少個節(jié)點能夠獲取最大的描述能力以及判別能力。本文基于能夠最大程度縮減原始高維輸入樣本與重構(gòu)后的輸入樣本之間的誤差來提取部分特征,，以此來提高模型的整體判別性能,。

　　誤差計算方式如下：

　　其中，xi是原始的輸入樣本,，hjWji是重構(gòu)后的輸入樣本,。

　　W*=argminWR(14)

3實驗結(jié)果

　　實驗從兩方面來驗證最具判別能力轉(zhuǎn)換法（MDT）的有效性以及可行性。第一個實驗基于Iris數(shù)據(jù)庫,，通過對比Laplacian Score［7］方法與Data variance方法來驗證Fisher Score方法的優(yōu)越性能,；第二個實驗是基于Mnist數(shù)據(jù)庫來評估MDT算法。

　　3.1Iris數(shù)據(jù)庫

　　Iris數(shù)據(jù)庫也稱鳶尾花卉數(shù)據(jù)集,，是一類多重變量分析的數(shù)據(jù)集,。數(shù)據(jù)庫包含150個數(shù)據(jù)集，分為3類,，每類50個數(shù)據(jù),，每個數(shù)據(jù)包含4個屬性（F1：sepal length；F2：sepal width,；F3：petal length,；F4：petal width）。大量研究證明對分類起顯著作用的屬性為F3與F4,。

　　Data variance方法被認(rèn)為是最簡單的無監(jiān)督分類算法,，它可以作為一種對特征選擇與提取的標(biāo)準(zhǔn)之一，另一種標(biāo)準(zhǔn)是Laplacian Score,，它是根據(jù)Laplacian Eigenmaps與Locality reserving Projection來評判的,。實驗結(jié)果如圖2所示。

　　圖2顯示,，根據(jù)Data variance標(biāo)準(zhǔn),，特征排序為：F3，F(xiàn)4,，F(xiàn)1,，F(xiàn)2；根據(jù)Laplacian Score排序結(jié)果為：F4,，F(xiàn)3,，F(xiàn)1，F(xiàn)2,；而根據(jù)Fisher Score排序結(jié)果為：F3,，F(xiàn)4,，F(xiàn)1，F(xiàn)2,。由此可知,，F(xiàn)isher Score能夠?qū)崿F(xiàn)比較好的特征評估。

　　3.2Mnist數(shù)據(jù)庫

　　Mnist數(shù)據(jù)庫包含有60 000個訓(xùn)練樣本和10 000個測試樣本,，每個樣本大小為28×28,，共分為10類。

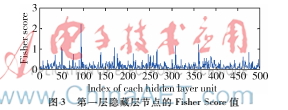
　　本實驗通過對比深度信念網(wǎng)絡(luò)（DBN）不同隱層節(jié)點數(shù)目發(fā)現(xiàn),，當(dāng)?shù)谝浑[層節(jié)點為500,、第二隱層節(jié)點為2 000時,，模型訓(xùn)練效果最好,，誤差最低，結(jié)果如表1表示,?；谠撟顑?yōu)結(jié)構(gòu)，我們希望MDT算法能夠進(jìn)一步降低模型分類誤差,。首先計算出第一層隱藏層中每一個節(jié)點的Fisher Score值,，如圖3所示。

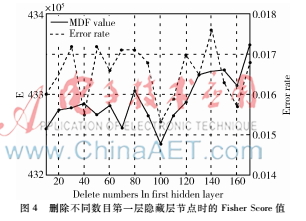
　　然后,，圖4展示了依次刪除第一層隱藏層不同節(jié)點數(shù)目后模型的錯誤率以及MDF值,。最后，發(fā)現(xiàn)刪除100個節(jié)點時,，MDF值最小并且模型的錯誤率也達(dá)到最小,。　　

4結(jié)論

　　本文提出了一種新穎的構(gòu)建DBN模型結(jié)構(gòu)的算法,，其基于Fisher準(zhǔn)則以及最大判別能力轉(zhuǎn)換法來動態(tài)地刪除隱層節(jié)點以達(dá)到優(yōu)化結(jié)構(gòu)的目的,，不同于現(xiàn)有的各種針對DBN模型所做的規(guī)則化算法?；诙鄠€數(shù)據(jù)庫的實驗結(jié)果也證實了本算法確定能夠獲得比較好的隱層節(jié)點數(shù)目,。

參考文獻(xiàn)

　　［1］ HINTON G E,SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks［J］. Science, 2006, 313(5786):504-507.

　?。?］ SALAKHUTDINV R, HINTON G. Semantic hashing［J］. International Journal of Approximate Reasoning, 2009, 50(7):969-978.

　?。?］ HINTON G E, SRIVASTAVA N,KRIZHEVSKY A, et al. Improving neural networks by preventing coadaptation of feature detectors［J］. Computer Science, 2012, 3(4):212-223.

　　［4］ SRIVASTAVA N. Improving neural networks with dropout［J］. Journal of Chemical Information and Modeling, 2015, 53(9):1689-1699.

　?。?］ HINTON G E,OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets［J］. Neural Computation, 1960, 18(7):1527-1554.