朱桂林,張棟良,陳輝
(上海電力學(xué)院 自動(dòng)化工程學(xué)院,上海市電站自動(dòng)化技術(shù)重點(diǎn)實(shí)驗(yàn)室, 上海 200090)
摘要:針對(duì)同一物體不同視角下獲得的三維點(diǎn)云數(shù)據(jù),提出一種基于改進(jìn)特征點(diǎn)對(duì)選取的三維點(diǎn)云配準(zhǔn)方法。在歐氏距離的基礎(chǔ)上選取與目標(biāo)點(diǎn)最近的三點(diǎn)均值為對(duì)應(yīng)點(diǎn),并應(yīng)用鄰域比值法來(lái)剔除錯(cuò)誤點(diǎn),結(jié)合Kd tree提高搜索速度,實(shí)現(xiàn)最終點(diǎn)云配準(zhǔn)。實(shí)驗(yàn)結(jié)果表明,該方法具有可行性,相比傳統(tǒng)ICP算法,其匹配精度和效率明顯提升。
關(guān)鍵詞:點(diǎn)云配準(zhǔn);ICP算法;最近點(diǎn)選取;錯(cuò)誤點(diǎn)剔除
中圖分類(lèi)號(hào):TP391文獻(xiàn)標(biāo)識(shí)碼:ADOI: 10.19358/j.issn.1674-7720.2017.01.022
引用格式:朱桂林,張棟良,陳輝. 基于改進(jìn)特征點(diǎn)對(duì)選取的三維點(diǎn)云配準(zhǔn)[J].微型機(jī)與應(yīng)用,2017,36(1):73-75.
0引言
利用激光掃描儀對(duì)建筑物進(jìn)行掃描,得到其點(diǎn)云信息,從而建立物體的三維模型,成為當(dāng)下研究的熱點(diǎn)[1]。但在實(shí)際操作中往往受到各種限制,無(wú)法一次性精準(zhǔn)地獲得待測(cè)物體的全部點(diǎn)云信息。為了在后期重建過(guò)程中得到較為完整的三維模型,實(shí)際測(cè)量中需要對(duì)待測(cè)物體進(jìn)行多角度、多次數(shù)的測(cè)量并且通過(guò)點(diǎn)云配準(zhǔn)將獲得的點(diǎn)云數(shù)據(jù)變換到同一坐標(biāo)中[2]。
針對(duì)點(diǎn)云配準(zhǔn)過(guò)程,迭代最近點(diǎn)算法(Iterative Closest Point,ICP)[3]是目前比較經(jīng)典的配準(zhǔn)方法。其優(yōu)點(diǎn)是對(duì)初始點(diǎn)云形狀要求低,配準(zhǔn)過(guò)程簡(jiǎn)單,結(jié)果相對(duì)收斂。但是該算法也存在著一些不足,如:要求待配準(zhǔn)兩片點(diǎn)云的數(shù)據(jù)為包含關(guān)系,兩片點(diǎn)云中的數(shù)據(jù)點(diǎn)滿(mǎn)足一一對(duì)應(yīng)關(guān)系;其次隨著點(diǎn)云數(shù)量的增加計(jì)算代價(jià)也相應(yīng)增加;最后在對(duì)應(yīng)點(diǎn)尋找過(guò)程中,僅僅假設(shè)兩片點(diǎn)云中歐氏距離最近的點(diǎn)為所求的對(duì)應(yīng)點(diǎn),由于這種假設(shè)過(guò)于理想化,在實(shí)際操作過(guò)程中可能會(huì)出現(xiàn)錯(cuò)誤的對(duì)應(yīng)點(diǎn),使配準(zhǔn)陷入局部最小值導(dǎo)致配準(zhǔn)失敗。針對(duì)傳統(tǒng)ICP算法的不足,國(guó)內(nèi)外學(xué)者在配準(zhǔn)策略、配準(zhǔn)元素、錯(cuò)誤點(diǎn)剔除以及誤差度量等方面對(duì)算法進(jìn)行了改進(jìn)與優(yōu)化,使傳統(tǒng)ICP算法在性能方面得到提高[47]。
本文在三維點(diǎn)云配準(zhǔn)過(guò)程中分以下兩步:
(1)提出了一種改進(jìn)的特征點(diǎn)對(duì)選取方法,過(guò)程采用Kd tree查找最近點(diǎn)以提高搜索效率。對(duì)于原始點(diǎn)云中的一點(diǎn),尋找其在目標(biāo)點(diǎn)云中歐氏距離最近的三點(diǎn)并計(jì)算三點(diǎn)的平均值,以此作為對(duì)應(yīng)點(diǎn),然后利用鄰域比值的方法來(lái)剔除誤匹配點(diǎn),提高匹配精度,最后結(jié)合四元法[89]求取旋轉(zhuǎn)矩陣R及平移向量T。
(2)根據(jù)計(jì)算得到的初始矩陣R及平移向量T,利用ICP算法對(duì)兩片點(diǎn)云進(jìn)行配準(zhǔn)。
1算法過(guò)程
1.1對(duì)應(yīng)點(diǎn)對(duì)選取和剔除錯(cuò)誤點(diǎn)對(duì)
(1)對(duì)應(yīng)點(diǎn)對(duì)求取
利用Kd tree計(jì)算點(diǎn)集P中任一點(diǎn)pi(i=1,2,...)在目標(biāo)點(diǎn)集Q中與其歐氏距離最近的三個(gè)點(diǎn)q1、q2、q3,分別計(jì)算三點(diǎn)x、y、z的均值構(gòu)成新的坐標(biāo)(=()),pi與構(gòu)成對(duì)應(yīng)點(diǎn)對(duì)(pi)。
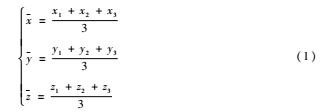
(2)錯(cuò)誤點(diǎn)對(duì)剔除
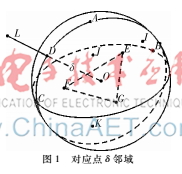
點(diǎn)集采集過(guò)程中不可避免地引入噪聲點(diǎn),因此在對(duì)應(yīng)點(diǎn)的計(jì)算過(guò)程中可能會(huì)產(chǎn)生錯(cuò)誤對(duì)應(yīng)點(diǎn)對(duì),本文采用鄰域點(diǎn)集比值法來(lái)檢驗(yàn)對(duì)應(yīng)點(diǎn)對(duì)是否符合標(biāo)準(zhǔn),并剔除錯(cuò)誤點(diǎn)對(duì)。由對(duì)應(yīng)關(guān)系可知,如果兩個(gè)點(diǎn)是對(duì)應(yīng)點(diǎn)則其在各自δ鄰域內(nèi)所包含的點(diǎn)數(shù)應(yīng)該近似相等。實(shí)驗(yàn)過(guò)程中在點(diǎn)云P和點(diǎn)云Q內(nèi)分別計(jì)算pi與以δ為半徑所構(gòu)成鄰域內(nèi)點(diǎn)的個(gè)數(shù)m和n。若mn=γ(0.9≤γ≤1.1),保留對(duì)應(yīng)點(diǎn)對(duì),否則剔除。如下圖1。
1.2四元數(shù)法求配準(zhǔn)矩陣R和T
對(duì)于原始點(diǎn)云數(shù)據(jù),在求取旋轉(zhuǎn)矩陣R和平移向量T時(shí),采用四元數(shù)法,其計(jì)算過(guò)程如下:
(1) 分別計(jì)算點(diǎn)集{pi}和點(diǎn)集{qi}的質(zhì)心:

(5)求K的特征值并且求解最大特征值所對(duì)應(yīng)的單位特征向量d,d=[d1d2d3d4]T
(6)求解旋轉(zhuǎn)矩陣R
![YZ(QHR3[]()%R4LGTGRR75O.png YZ(QHR3[]()%R4LGTGRR75O.png](http://files.chinaaet.com/images/2017/03/02/6362407783596167248132463.png)
(7)根據(jù)R與T的對(duì)應(yīng)關(guān)系求取平移向量T
T=μq-Rμp(7)
1.3改進(jìn)ICP算法的配準(zhǔn)過(guò)程
ICP算法在本質(zhì)上是使用最小二乘的方法對(duì)待配準(zhǔn)的點(diǎn)云數(shù)據(jù)進(jìn)行最優(yōu)匹配。計(jì)算過(guò)程中重復(fù)進(jìn)行選擇對(duì)應(yīng)關(guān)系點(diǎn)對(duì),計(jì)算最優(yōu)旋轉(zhuǎn)矩陣R和平移矢量T,直到滿(mǎn)足正確的收斂精度函數(shù)E并使E達(dá)到最小值。
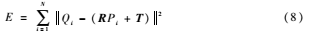
式中,Pi為原數(shù)據(jù)的初始點(diǎn)集;Qi為Pi對(duì)應(yīng)目標(biāo)數(shù)據(jù)點(diǎn)集的最近點(diǎn);R為3×3旋轉(zhuǎn)矩陣;T為3×1平移矢量。
配準(zhǔn)過(guò)程具體如下:
(1) 讀取初始點(diǎn)云并在初始點(diǎn)云中選取點(diǎn)集pi;
(2) 利用Kd tree對(duì)點(diǎn)集p中任一點(diǎn)pi計(jì)算其在點(diǎn)集q內(nèi)歐氏距離最近的三個(gè)點(diǎn)q1、q2、q3,并計(jì)算,過(guò)程對(duì)應(yīng)點(diǎn)對(duì)(pi);
(3)采用鄰域點(diǎn)集比值法剔除不符合條件的對(duì)應(yīng)點(diǎn);
(4)采用四元數(shù)法計(jì)算旋轉(zhuǎn)矩陣R和平移矢量T;
(5)迭代終止判斷:若ek-ek+1<ε,則終止迭代,否則重復(fù)(2)~(5)直至結(jié)果滿(mǎn)足收斂條件。其中ε表示大于零的閾值。
2實(shí)驗(yàn)論證
本實(shí)驗(yàn)采用的實(shí)驗(yàn)數(shù)據(jù)來(lái)自斯坦福兔子(Stanford Bunny),分別選取不同視角下的兩組點(diǎn)云數(shù)據(jù)作為原始點(diǎn)云和目標(biāo)點(diǎn)云,兩片點(diǎn)云的數(shù)量分別為35 947和30 379。實(shí)驗(yàn)平臺(tái)為:CPU 2.70 GHz,內(nèi)存4 GB,Windows7 32位操作系統(tǒng);算法在MATLAB 2011b環(huán)境中實(shí)現(xiàn),實(shí)驗(yàn)選取的ε=0.005。
實(shí)驗(yàn)過(guò)程中為了進(jìn)一步驗(yàn)證本文方法的可行性,減少中間誤差,在與傳統(tǒng)ICP算法比較過(guò)程中,本文分別從迭代次數(shù)和迭代點(diǎn)云數(shù)量?jī)煞矫妫锤牡螖?shù)以及更改點(diǎn)云數(shù)量)進(jìn)行驗(yàn)證。
2.1迭代次數(shù)
為消除實(shí)驗(yàn)過(guò)程中次數(shù)對(duì)結(jié)果的影響,對(duì)于Stanford Bunny操作過(guò)程中分別選取迭代次數(shù)為5次、10次以及15次作為一組參照進(jìn)行對(duì)比驗(yàn)證,實(shí)驗(yàn)結(jié)果如表1。表1不同迭代次數(shù)下兩種方法配準(zhǔn)效果原始數(shù)據(jù)點(diǎn)云圖ICP配準(zhǔn)效果圖本文配準(zhǔn)方法效果圖迭代次數(shù)5次10次15次從表1可得出,在使用相同的初始點(diǎn)云數(shù)據(jù)情況下:(1)迭代次數(shù)相同時(shí),本文所采用的改進(jìn)ICP算法所得出的配準(zhǔn)效果明顯優(yōu)于傳統(tǒng)ICP算法;(2)隨著迭代次數(shù)增加,傳統(tǒng)ICP算法配準(zhǔn)效果逐級(jí)優(yōu)化,但是采用改進(jìn)算法所得到的配準(zhǔn)圖像逐級(jí)優(yōu)化效果更加明顯。
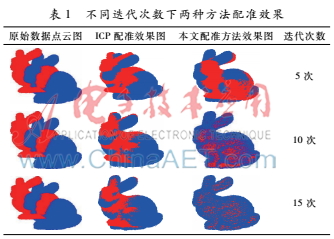
為了進(jìn)一步比較改進(jìn)算法相對(duì)于傳統(tǒng)ICP算法的優(yōu)勢(shì),在基于不同迭代次數(shù)情況下分別從配準(zhǔn)時(shí)間以及配準(zhǔn)誤差兩個(gè)方面進(jìn)行列表對(duì)比,本文采用均方根誤差[10](Root Mean Square,RMS)來(lái)表示配準(zhǔn)誤差,對(duì)比情況如表2。

從表2可以看出,在同一迭代次數(shù)下改進(jìn)算法與傳統(tǒng)ICP算法相比在配準(zhǔn)誤差以及配準(zhǔn)時(shí)間上都得到了明顯優(yōu)化,這種優(yōu)化隨著迭代次數(shù)的增加變得更加明顯,例如迭代次數(shù)為5時(shí),傳統(tǒng)ICP算法配準(zhǔn)時(shí)間為240.37 s,配準(zhǔn)誤差為0.122 4,而改進(jìn)的ICP算法配準(zhǔn)時(shí)間為22.70 s,配準(zhǔn)誤差為0.066 0;當(dāng)?shù)螖?shù)為15時(shí),傳統(tǒng)ICP算法配準(zhǔn)時(shí)間為610.45 s,配準(zhǔn)誤差為0.037 6,此時(shí)改進(jìn)ICP算法配準(zhǔn)時(shí)間僅為40.89 s,配準(zhǔn)誤差為0.002 4。綜上,無(wú)論是在同一迭代次數(shù)的橫向?qū)Ρ冗€是在不同迭代次數(shù)的縱向?qū)Ρ戎校疚牟捎玫呐錅?zhǔn)方法在配準(zhǔn)效果、配準(zhǔn)時(shí)間以及配準(zhǔn)誤差上都要明顯優(yōu)于傳統(tǒng)ICP算法。
2.2迭代點(diǎn)云數(shù)量
為了消除點(diǎn)云數(shù)量對(duì)兩種方法產(chǎn)生的誤差,本文在基于Bunny數(shù)據(jù)基礎(chǔ)上,選取初始點(diǎn)云數(shù)量分別為400點(diǎn)、3 600點(diǎn)、6 400點(diǎn)以及32 400點(diǎn),并在迭代次數(shù)同為15次的基礎(chǔ)上進(jìn)行對(duì)比驗(yàn)證,結(jié)果如表3。
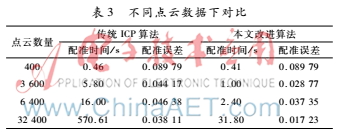
根據(jù)表3,在初始點(diǎn)云數(shù)較少的情況下,改進(jìn)方法與傳統(tǒng)ICP方法相比在配準(zhǔn)時(shí)間和配準(zhǔn)誤差上均有進(jìn)步,但差別并不明顯,如在點(diǎn)云數(shù)為400點(diǎn)時(shí)二者配準(zhǔn)時(shí)間相差為0.05 s,在小數(shù)點(diǎn)后精確5位的情況下配準(zhǔn)誤差同為0.089 79。但是隨著點(diǎn)云數(shù)量的增加,改進(jìn)的ICP算法與傳統(tǒng)ICP算法相比具有明顯優(yōu)勢(shì),例如當(dāng)初始點(diǎn)云數(shù)量為6 400時(shí),傳統(tǒng)ICP算法配準(zhǔn)時(shí)間為16.00 s,配準(zhǔn)誤差為0.046 38,而改進(jìn)ICP算法配準(zhǔn)時(shí)間僅為2.40 s,配準(zhǔn)誤差為0.037 35;當(dāng)初始點(diǎn)云數(shù)量為32 400時(shí),改進(jìn)算法優(yōu)勢(shì)更為突出。由表3數(shù)據(jù)分析可知,在不同點(diǎn)云數(shù)量下改進(jìn)的ICP方法與傳統(tǒng)ICP算法相比,無(wú)論是在配準(zhǔn)時(shí)間還是在配準(zhǔn)誤差上都具有明顯改進(jìn),并且隨著初始點(diǎn)云數(shù)量的增加,本文改進(jìn)方法的優(yōu)勢(shì)彰顯得更為明顯。
3結(jié)論
本文針對(duì)三維點(diǎn)云數(shù)據(jù)配準(zhǔn)耗時(shí)長(zhǎng)、精度低兩方面的不足進(jìn)行了相應(yīng)改進(jìn),提出了一種改進(jìn)特征點(diǎn)對(duì)選取方法,通過(guò)在經(jīng)典點(diǎn)云Standford Bunny數(shù)據(jù)集上與采用傳統(tǒng)ICP算法的配準(zhǔn)結(jié)果相比,在配準(zhǔn)時(shí)間和配準(zhǔn)精度上都有明顯提高。本文對(duì)點(diǎn)云數(shù)據(jù)配準(zhǔn)的優(yōu)化,對(duì)后續(xù)點(diǎn)云網(wǎng)格化以及場(chǎng)景重建提供了算法基礎(chǔ)。
參考文獻(xiàn)
[1] TANG P B,HUBER D, AKINCI B, et al.Automatic reconstruction of asbuilt building information models from laserscanned point clouds:a review of related techniques[J].Automation in Construction,2010,19(7):829-843.
[2] 韓寶昌,曹俊杰,蘇志勛.一種區(qū)域?qū)哟紊系淖詣?dòng)點(diǎn)云配準(zhǔn)算法[J].計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào), 2015,27(2):313-
319.
[3] BESL P J, MCKAY N D. Method for registration of 3D shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):239-256.
[4] Guo Yu, BENNAMOUN M, SHOEL F, et al.3D object recognition in cluttered scenes with local surface features: a survey[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014,36(11):2270-2287.
[5] 楊小青, 楊秋翔,楊劍.基于法向量改進(jìn)的ICP算法[J].計(jì)算機(jī)工程與設(shè)計(jì), 2016, 37(1):169-173.
[6] 許斌, 李忠科,呂培軍,等.基于特征的點(diǎn)云精確配準(zhǔn)算法[J].計(jì)算機(jī)應(yīng)用與軟件, 2013,30(11):112-115.
[7] 張曉娟,李忠科,王先澤,等.基于特征點(diǎn)和改進(jìn)ICP的三維點(diǎn)云數(shù)據(jù)配準(zhǔn)算法[J].傳感器與微系統(tǒng), 2012,31(9):116118.
[8] KUIPERS J B. Quaternions and rotation sequences[M].Sofia: Coral Press,2000:127-143.
[9] HORN B K P.Closed-form solution of absolute orientation using unit quaternions[J].Optical Society of America, 1987,4(4):629-642.
[10] EGGERT D W, LORUSSO A.Estimating 3D rigid body transformations a comparison of four major algorithms[J].Machine Vision and Applications, 1997,9(5):272-290.

