張芝賢,，程繼坤,，武旭娟

　　（沈陽航空航天大學 電子與通信工程學院,，遼寧 沈陽,，110136）

       摘要：雙目立體視覺測量系統(tǒng)是工業(yè)測量中的重要手段，三維重建是雙目立體視覺測量體統(tǒng)中非常重要的一環(huán),?；谝暡钤淼膫鹘y(tǒng)三維重建模型是對雙目立體視覺系統(tǒng)的一種理想化抽象。通過分析由平面到三維點的實際映射過程,，提出了一種更加符合實際數(shù)據的三維重建模型,，異面直線公垂線三維重建方法。該方法通過計算兩攝像機光心與其各自像點構成的兩條空間直線的公垂線,，即兩條異面直線的最小距離點來定位三維空間點,，且其最小距離參數(shù)可有效判斷誤匹配點。通過實驗對該方法進行了驗證,。結果表明該方法可達到傳統(tǒng)視覺三維重建方法的測量精度,，并可有效判斷匹配點是否為誤匹配點。

　　關鍵詞：雙目立體視覺測量,；異面直線公垂線,；誤匹配點；三維立體重構

　　中圖分類號：TP391文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.04.024

　　引用格式：張芝賢，程繼坤,，武旭娟.公垂線法雙目立體視覺三維重建［J］.微型機與應用,，2017,36（4）：80-83.

0引言

　　雙目立體視覺測量是一種基于視差原理的三維非接觸測量技術。由兩臺攝像機在不同的角度下同時獲取待測目標的圖像,，然后利用特征點的圖像坐標根據測量模型重建其三維坐標,，最后通過擬合這些特征點獲取待測目標的三維幾何信息。雙目立體視覺重建技術已經深入到人們生活,、生產和工作的方方面面,，具有重要的理論意義和實用價值。它所涉及的知識面很廣,，是一種綜合性的技術,，有廣闊的發(fā)展前途和廣泛的應用前景［1］。在三維立體重構中,空間點作為三維結構最為基本的組成單位,，在理論方面能夠從點構成線,，從線構成面，隨后通過各個面來形成三維空間結構,。所以,，測量空間點的具體坐標是最為基本的雙目立體視覺內容。雙目立體三維重構也是基于點的三維信息的獲取,。

　　雙目立體視覺利用三角幾何相關原理來對視差進行計算進而獲得物象在三維空間上的信息［2］,。為理解雙目立體的視覺原理，通常假設存在一個結構非常簡單的雙目視覺系統(tǒng)［3］,，兩個攝像機光軸平行并且它們的內參完全相同,，如圖1所示,。這個系統(tǒng)的基線（兩個攝像機光心之間的連線）與第一個攝像機的x軸一致,。

　　而對于構建一般雙目視覺系統(tǒng)，無法嚴格保證兩相機坐標系嚴格平行,。一般測量模型［4］更便于理解雙目立體視覺結構,。如圖2所示，該模型不需要兩個相機坐標系嚴格平行,。

　　對于以上兩種測量模型,，都首先需要進行標定獲得相機的內外參數(shù)，區(qū)別在于理想測量模型需要根據內外參數(shù)將測量系統(tǒng)映射轉化為理想測量系統(tǒng),，而一般測量模型僅需要對圖像做畸變校正,，而后直接利用兩相機的相對位姿關系求得三維點信息。

　　然而由于實際的鏡頭并不是理想的透視成像,，而是帶有不同程度的畸變,，圖像中存在噪聲的干擾影響特征點提取精度等原因，使得空間點所成的像并不是在線性模型所描述的位置,，在實際數(shù)據中這兩條直線并非交于一點而是構成空間異面直線,。另一方面,，對于匹配錯誤的同名點，以上兩種算法的重構過程無法判斷該組同名點是否匹配有誤,。而誤匹配在所有的匹配算法中都是無法完全避免的［5］,。由于誤匹配點的不確定性可能會導致重構三維空間點嚴重偏離實際點，大大影響了系統(tǒng)測量精度,。

　　根據雙目立體視覺的實際數(shù)據,，在一般測量模型基礎上，可將兩條視線即兩相機光心與各自像點的連線視為兩條空間異面直線,。通過求取這兩條異面直線以及異面直線公垂線［6］,，可確定三維重構點的最佳估計位置，同時可根據距離參數(shù)判斷該點是否為誤匹配點,。

1公垂線法三維立體重建

　　1.1攝像機標定與點的坐標系轉換

　　圖像與三維信息之間的對應關系是由攝像機成像的幾何模型決定的,這些幾何模型參數(shù)就是攝像機參數(shù),求解攝像機參數(shù)的過程即攝像機標定的過程［7］,。攝像機標定是雙目立體視覺系統(tǒng)中的重要一環(huán)，是三維立體重構的基礎環(huán)節(jié),。通過攝像機標定一方面獲得成像幾何模型的結構參數(shù)用于三維立體信息的重構,，另一方面是對攝像機存在的鏡頭畸變進行校正確保測量精度。

　　研究中采用張正友提出的基2D平面標定板的標定算法［8］,，并在其原有算法僅考慮鏡像畸變基礎上考慮了切向畸變帶來的影響,，使得畸變校正結果更理想，精度更高,。

　　其中,，k1、k2為徑向畸變系數(shù),，p1,、p2為切向畸變系數(shù)，pd(xd, yd)為實際的圖像坐標,，pu(xu, yu)為不考慮鏡頭畸變的線性模型下的圖像坐標,，即為畸變校正后的圖像坐標。

　　標定獲得相機的內部參數(shù)以及兩相機坐標系間的變換關系H,。根據內參可以確定相機光心與像點在各自坐標下的坐標,，然后根據兩相機坐標系的轉換關系H將所有點統(tǒng)一到同一坐標系下［9］。這里根據方程(2)將所有三維點統(tǒng)一到左相機坐標系下,。

　　其中PR為空間點在右相機坐標系下的空間坐標,，PL為空間點在左相機坐標系下的坐標R為旋轉矩陣，t為右相機坐標系到左相機坐標系的一個平移量,。

　　由此可由一對同名點以及相機各自光心四個點構成雙目立體視覺的兩條視線,，并可將這兩條異面直線在同一坐標系下表示。

　　1.2公垂線法立體重構

　　如圖3所示，兩條視線構成一對異面直線,?？臻g異面直線的最小距離點即為兩條異面直線的公垂線與兩條異面直線的交點。這里是以左相機坐標系為作為系統(tǒng)坐標系,。因此選取左相機的視線與公垂線的交點為三維重構的最佳估計點,。

　　根據P1、O1與P2,、O2構成的兩條視線的直線為：

　　公垂線兩視線的交點分別為：

　　M(x1+m1t1,y1+n1t1,z1+p1t1)

　　N(x2+m2t2,y2+n2t2,z2+p2t2)

　　兩條異面直線的最小距離參數(shù)：

　　選取左相機視線與公垂線交點M為最佳三維重構點,。距離參數(shù)Dist為兩條視線的最小距離。

　　與傳統(tǒng)方法相比公垂線法立體重構除獲得三維重構點外,，還可獲得一個異面直線距離參數(shù),。在理想情況下兩個特征點匹配正確時該距離參數(shù)為零。而實際中匹配正確的也會存在微小的位置偏差,，但這種偏差基本是亞像素級的,，雖然會使距離參數(shù)不為零，但其值在會在一個很小的范圍之內,。當重構點為誤匹配點時,，匹配點對的誤差則是不可預知的，至少是像素級別的,，其可能是幾個,、幾十個甚至上百個像素點，因而距離參數(shù)數(shù)值也急劇增大,。正是因為正確匹配點與誤匹配點在距離參數(shù)數(shù)值上的差異,，所以可將該值作為對誤匹配點進行甄別的一個有效手段。

2三維重構實驗及精度評價

　　本文標定過程采用寬度為500 mm的 Halcon標定板對雙目立體視覺系統(tǒng)進行標定,。標定獲得相機內參如表1,、表2所示，左右兩相機的相對位置關系如表3所示,。

　　實驗中標定板精度在1 μm以內,，因此通過提取標定板中的標志點進行匹配三維重構來驗證公垂線三維重構點的距離精度。實驗中拍攝了標定板8種不同姿態(tài),，并對距離為375 mm的兩標志點進行三維重構，如圖4所示,。

　　利用不同三維重構算法對該對同名點進行三維重構求取距離,，并對三種方法進行精度分析對比，如表4所示,。利用公垂線法三維重構同時可獲得16個點重構的距離參數(shù)Dist,。而后在在雙目系統(tǒng)下利用匹配算法進行特征點的提取與匹配，通過人工識別找出自動匹配點對中的誤匹配點。同樣對重構獲得距離參數(shù)Dist,，并將與正確匹配點對的距離參數(shù)作比較,，如表5所示。

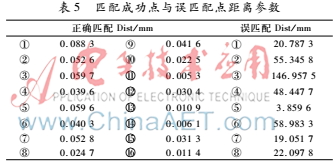
　　由表5可知,，正確匹配點與誤匹配點對距距離參數(shù)Dist有明顯差異,且其值與系統(tǒng)精度重構一致,，在10-5 m波動。而誤匹配點由于誤匹配的隨機性則距離參數(shù)具有較大波動性,，并且其距離參數(shù)要遠遠大于求取正確匹配點的距離參數(shù),，所以根據該依據可有效區(qū)分匹配點中的誤匹配點。

3結論

　　本文基于傳統(tǒng)雙目立體視覺重構方法提出了一種新公垂線雙目立體視覺重構方法,。通過實驗驗證了該方法可達到傳統(tǒng)的三維立體重構方法對空間點的重構精度,。同時利用該方法三維點重構過程中獲得的異面直線的距離參數(shù)來對匹配點進行判斷。通過設置合適閾值可自動篩選出重構點中的誤匹配點將其去除,，不僅可提高測量效率,，而且進一步保證了測量精度。

參考文獻

　?。?］ FUSIELLO A.Uncalibrated euclidean reconstruction:a review［J］.Image and Vision Computing, 2000, 18(67): 555563.［2］ 馬頌德,張正友. 計算機視覺計算機理論與算法基礎［M］.北京: 科學出版社,1998.

　?。?］ 馬桂珍,諶海新,馬丙辰.基于雙目視覺的手術器械跟蹤定位技術［J］.微計算機應用,2005,26(2)：181183.

　　［4］ 邾繼貴,于之靖.視覺測量原理與方法［M］.北京：機械工業(yè)出版社,，2011.

　?。?］ 劉晶晶.基于雙目立體視覺的三維定位技術研究［D］.武漢:華中科技大學,2007.

　　［6］ 呂林根,許子道.解析幾何［M］.北京:高等教育出版社,2007.

　?。?］ 賈云得.機器視覺 ［M］.北京：科學出版社,2005.

　?。?］ Zhang Zhengyou. A flexible new technique for camera  calibration ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence,2000，22（11）：1330 1334.

　?。?］ STEGER C,ULRICH M,WIEDEMANN C.機器視覺算法與應用［M］.楊少榮,，吳迪靖，段德山,，譯.北京：清華大學出版社,，2008．

　　［10］ LENZ R K,TSAI R Y. Techniques for calibration of the scale factor and image center for high accuracy 3D machine vision metrology ［C］. Proceedings of IEEE International Conference on Robotics and Automation, Washington DC：IEEE,，1987：6875.