杜青

　　（南京工程學(xué)院 計(jì)算機(jī)工程學(xué)院,，江蘇 南京 211167）

       摘要：本文以C++語言設(shè)計(jì)了大整數(shù)類,，在類中以數(shù)組存儲(chǔ)大整數(shù)，同時(shí)借鑒分治算法思想實(shí)現(xiàn)了大整數(shù)的乘法運(yùn)算,。算法中將被乘數(shù)與乘數(shù)按照相同位數(shù)進(jìn)行分組,，通過對(duì)每組較小數(shù)值整數(shù)進(jìn)行乘法和加法運(yùn)算而得到大整數(shù)相乘的積。該程序在VC++2015開發(fā)平臺(tái)調(diào)試通過,。測(cè)試結(jié)果表明,，當(dāng)每個(gè)分組數(shù)據(jù)位數(shù)多時(shí)，運(yùn)算速度顯著提高,。

　　關(guān)鍵詞：大整數(shù),；大整數(shù)相乘；分治算法,；類

　　中圖分類號(hào)：TP301文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2017.02.003

　　引用格式：杜青.基于類的大整數(shù)乘法運(yùn)算的實(shí)現(xiàn)［J］.微型機(jī)與應(yīng)用,，2017,36（2）：8-9，13.

　　0引言

　　大整數(shù)是指數(shù)值很大,、超出計(jì)算機(jī)整數(shù)表達(dá)和處理范圍的非負(fù)整數(shù),。一般計(jì)算機(jī)能夠處理的整數(shù)有三種類型，即2字節(jié)（16 bit）,、4字節(jié)（32 bit）和8字節(jié)（64 bit）整數(shù),，其中8字節(jié)整數(shù)取值范圍最大，8字節(jié)無符號(hào)整數(shù)取值范圍是：0～264-1,。當(dāng)整數(shù)值超過整數(shù)范圍的最大值264-1時(shí),，計(jì)算機(jī)無法直接處理。

　　大整數(shù)的乘法運(yùn)算在密碼學(xué)等領(lǐng)域有著廣泛的應(yīng)用,。如著名的公鑰加密算法RSA算法,，大整數(shù)相乘是其中必不可少的運(yùn)算，由于運(yùn)算中使用的密鑰推薦位數(shù)為1 024位,，為了達(dá)到更高安全級(jí)別,，密鑰長(zhǎng)度甚至達(dá)到上萬位,，遠(yuǎn)遠(yuǎn)超出計(jì)算機(jī)所能直接處理的64 bit的整數(shù)范圍。

　　當(dāng)需要對(duì)大整數(shù)進(jìn)行乘法運(yùn)算時(shí),，面臨的問題是：如何存儲(chǔ)大整數(shù)以及如何提高大整數(shù)乘法的運(yùn)算速度,。已有的實(shí)現(xiàn)大整數(shù)乘法的程序中，有的采用累加的方式,，將被乘數(shù)重復(fù)相加若干次,，累加的次數(shù)等于乘數(shù)；有的按照手算的形式,，將乘數(shù)逐位與被乘數(shù)相乘,，并將結(jié)果做位移運(yùn)算后按位求和［1］。當(dāng)被乘數(shù)與乘數(shù)位數(shù)很多時(shí),，這些方法運(yùn)算時(shí)間長(zhǎng),。

　　本文以C++語言設(shè)計(jì)了一個(gè)大整數(shù)類，在類中以數(shù)組存儲(chǔ)大整數(shù),，同時(shí)借鑒分治算法的思想［2］,，將數(shù)值很大的大整數(shù)分解為若干組數(shù)值較小的整數(shù),，通過對(duì)每組較小數(shù)值整數(shù)的運(yùn)算得到大整數(shù)相乘的積,。程序在VC++2015開發(fā)平臺(tái)調(diào)試通過。

1大整數(shù)的存儲(chǔ)

　　由于大整數(shù)位數(shù)多,，若用字符串形式表示,，在做運(yùn)算時(shí)，首先要將表示大整數(shù)的字符串轉(zhuǎn)換成數(shù)值,。轉(zhuǎn)換時(shí)考慮到大整數(shù)的數(shù)值一般超出整數(shù)的取值范圍,，所以采用整型數(shù)組存儲(chǔ)其值［3］。

　　以下給出了大整數(shù)類BigInt的聲明,，類中的數(shù)據(jù)成員uint64_t 類型數(shù)組array用于存放大整數(shù),，uint64_t是64 bit無符號(hào)整數(shù)類型。轉(zhuǎn)換時(shí)從大整數(shù)字符串最低位開始,，每K個(gè)字符為一組,，最高位不足K個(gè)字符時(shí)補(bǔ)0，將每組字符轉(zhuǎn)換為一個(gè)數(shù)值較小的整數(shù),，每個(gè)較小整數(shù)存放到整型數(shù)組的一個(gè)元素中,。類中數(shù)據(jù)成員n為已存放了數(shù)據(jù)的元素個(gè)數(shù)，即分組數(shù),。類聲明代碼如下：

　　#define N 10000//數(shù)組大小

　　#define K 3//每個(gè)分組中包含的字符個(gè)數(shù)

　　class BigInt

　　{public:

　　BigInt();//無參構(gòu)造函數(shù),，將n置0

　　BigInt(string str);//轉(zhuǎn)換構(gòu)造函數(shù)

　　int compare(BigInt num); //比較類對(duì)象大小

　　friend BigInt operator*(BigInt num1, BigInt num2);//重載乘法運(yùn)算符

　　friend int operator>(BigInt num1, BigInt num2);

　　//重載大于運(yùn)算符

　　private:

　　uint64_t array［N］;//存放大整數(shù)的數(shù)組

　　int n;//存放了數(shù)據(jù)的元素個(gè)數(shù)

　　};

　　類中的轉(zhuǎn)換構(gòu)造函數(shù)實(shí)現(xiàn)了將大整數(shù)字符串分組，并將各組字符串轉(zhuǎn)換為數(shù)值存放到array數(shù)組中的操作,。轉(zhuǎn)換構(gòu)造函數(shù)的代碼如下：

　　BigInt::BigInt(string str) //將字符串轉(zhuǎn)換為數(shù)值

　　{int end = str.length() - 1, i;

　　uint32_ttemp,w;//w代表權(quán)重

　　n = 0;

　　i = end;//從最低位開始處理

　　while (i >= 0)

　　{temp = 0;w = 1;

　　for (int k =0;k<K;k++) //K個(gè)字符組成1個(gè)數(shù)

　　{if (str［i］ >= 0&&str［i］ <= 9)

　　{temp = temp + w*(str［i］ - 0);

　　w *= 10; i--;

　　if (i<0)break;

　　}

　　}

　　array［n］ = temp;n++;

　　}

　　for (i = n;i<N;i++) array［i］ = 0; //其他元素置0

　　}　

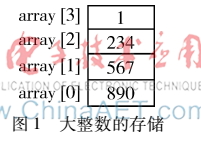
　　當(dāng)K=3時(shí),，字符串“1234567890”在數(shù)組array中存放的形式如圖1所示。

2大整數(shù)乘法的實(shí)現(xiàn)

　　2.1大整數(shù)乘法的算法

　　當(dāng)一個(gè)m位的大整數(shù)X與一個(gè)n位的大整數(shù)Y相乘時(shí)，如按照手算的方式進(jìn)行計(jì)算,，需要將Y的每一位與X的每一位相乘,，共要做m×n次數(shù)據(jù)相乘。如m,、n很大,，則數(shù)據(jù)相乘次數(shù)多，從而使整個(gè)乘法運(yùn)算時(shí)間長(zhǎng),。

　　為了解決這個(gè)問題,，利用分治法的思想，將X,、Y均分解為K位一組的整數(shù)［4］,，即X分解為…xi…x2x1x0，共(m+K-1)/K組數(shù)字,，Y分解為…yj…y2y1y0,，共 (n+K-1)/K組數(shù)字，運(yùn)算時(shí)將由Y分解得到的每一組整數(shù)yj與由X分解得到的每一組整數(shù)xi相乘,。

　　以K=3時(shí),，1234567890與1234567890做乘法運(yùn)算為例，如按手算方式進(jìn)行運(yùn)算,，需做10×10共100次數(shù)據(jù)相乘,，而若將被乘數(shù)與乘數(shù)分解為3位一組的數(shù)字，即各自分解為4組數(shù)字,，如圖2所示,，則只需要完成4×4共16次數(shù)據(jù)相乘，數(shù)據(jù)相乘次數(shù)大大減少,。在進(jìn)行分組數(shù)據(jù)相乘后,，再按組進(jìn)行數(shù)據(jù)相加，從而得到兩個(gè)大整數(shù)乘法運(yùn)算的積,。大整數(shù)分組運(yùn)算過程示意圖如圖2所示,。

　　當(dāng)K較大時(shí)，每組數(shù)據(jù)因位數(shù)增加而數(shù)值變大,，分組數(shù)目隨之減少,，分組數(shù)據(jù)乘法次數(shù)也減少。但當(dāng)K過大時(shí),，每組數(shù)據(jù)與其他組數(shù)據(jù)相乘時(shí)得到的中間結(jié)果可能會(huì)超出整型數(shù)據(jù)的最大值而導(dǎo)致數(shù)據(jù)溢出,。為了防止溢出情況的出現(xiàn)，K的取值不能太大,。由于uint64的最大值是264-1,，因此每組數(shù)字的最大值不能超過232-1,，即4 294 967 295，由此推斷,，每組數(shù)字不能超過9位,，即K要滿足：1≤K≤9。

　　2.2大整數(shù)乘法的實(shí)現(xiàn)

　　m位的大整數(shù)X與n位的大整數(shù)Y進(jìn)行乘法運(yùn)算時(shí),，將yj依次與xi相乘,，保留xi*yj%BASE為中間結(jié)果，yj*xi/BASE為進(jìn)位,，其中BASE的值等于10K,，是運(yùn)算的基［5］。兩個(gè)大整數(shù)相乘后得到的乘積的位數(shù)是m+n或m+n-1［6］,。

　　下面給出了實(shí)現(xiàn)大整數(shù)乘法運(yùn)算的函數(shù)定義,，該函數(shù)是乘法運(yùn)算符重載函數(shù)，已在BigInt類中聲明為友元,。該函數(shù)代碼如下：

　　#define BASE 1000 //運(yùn)算的基

　　BigInt operator*(BigInt num1, BigInt num2)

　　{BigInt temp1, temp2;

　　if (num2>num1)//保證被乘數(shù)大于乘數(shù)

　　{temp1=num1; num1=num2; num2=temp1;}

　　uint64_t num, c;//num存放中間結(jié)果,c為進(jìn)位

　　int maxi, mini, i, j;

　　maxi = num1.n; //被乘數(shù)分組數(shù)

　　mini = num2.n; //乘數(shù)分組數(shù)

　　for (i = 0;i<mini;i++)

　　{c = 0;//進(jìn)位初值為0

　　for (j = 0;j<maxi;j++)

　　{num = num1.array［j］ * num2.array［i］ + c;

　　temp2.array［j+i］+=num%BASE; //做一次

　　//分組相乘之后做分組加法

　　c = num / BASE;

　　if (temp2.array［j + i］ >= BASE)//判斷是

　　//否超出BASE

　　{temp2.array［j+i］=temp2.array［j+i］%BASE;

　　c++;//進(jìn)位加1

　　}

　　}

　　if (c) temp2.array［j + i］ += c; //有進(jìn)位時(shí)

　　}

　　temp2.n = maxi + mini - 1;//設(shè)置乘積的分組數(shù)

　　if (c) temp2.n++; //最后一次運(yùn)算有進(jìn)位時(shí)

　　return temp2;

　　}

　　以上實(shí)現(xiàn)大整數(shù)乘法的函數(shù)中,，做一次分組數(shù)據(jù)相乘之后，將得到的中間結(jié)果做分組加法運(yùn)算,，并且在做分組加法運(yùn)算時(shí),，要判斷加法運(yùn)算的結(jié)果是否溢出，若溢出,，將加法運(yùn)算結(jié)果對(duì)BASE取余數(shù),，同時(shí)進(jìn)位加1。

　　2.3運(yùn)行測(cè)試

　　在VC++2015開發(fā)平臺(tái)運(yùn)行程序,，測(cè)試時(shí)用兩個(gè)4 000位大整數(shù)做乘法，且使該乘法運(yùn)算重復(fù)執(zhí)行1 000次,，測(cè)試當(dāng)K取1,、2、3,、……,、9不同值時(shí)所花費(fèi)時(shí)間，得到結(jié)果如表1所示,。由表1可以看出,，K值增大，大整數(shù)乘法運(yùn)行時(shí)間大大減少,。

3結(jié)論

　　本文以C++類的方式實(shí)現(xiàn)了大整數(shù)的乘法運(yùn)算,，算法中根據(jù)分治法思想，將被乘數(shù)與乘數(shù)按照相同位數(shù)進(jìn)行分組,，通過對(duì)每組較小數(shù)值整數(shù)進(jìn)行運(yùn)算,，從而得到大整數(shù)相乘的結(jié)果,。該程序在VC++2015開發(fā)平臺(tái)調(diào)試通過。實(shí)驗(yàn)結(jié)果表明,，當(dāng)每個(gè)分組數(shù)據(jù)位數(shù)多時(shí),，乘法運(yùn)算速度顯著提高。

　　參考文獻(xiàn)

　?。?］ 周健,李順東,薛丹.改進(jìn)的大整數(shù)相乘快速算法［J］.計(jì)算機(jī)工程,2012,38(16):121-123.

　?。?］ 王曉東. 計(jì)算機(jī)算法設(shè)計(jì)與分析(第3版)［M］. 北京:清華大學(xué)出版社, 2014.

　　［3］ 楊燦,桑波.大整數(shù)乘法運(yùn)算的實(shí)現(xiàn)及優(yōu)化［J］.計(jì)算機(jī)工程與科學(xué),2013,35(3):183-190.

　?。?］ 王念平,金晨輝.用分治算法求大整數(shù)相乘問題的進(jìn)一步分析［J］.電子學(xué)報(bào),2008,36(1):133-135.

　?。?］ 李文化,董克家.大整數(shù)精確運(yùn)算的數(shù)據(jù)結(jié)構(gòu)與基選擇［J］.計(jì)算機(jī)工程與應(yīng)用,2006,42(32):24-26.

　　［6］ 劉覺夫,周娟.大整數(shù)運(yùn)算的基選擇［J］.華東交通大學(xué)學(xué)報(bào),2007,24(2):100102.