馬健超1,2，陳國棟1,2,，周霆1,2

　?。?.福州大學(xué) 物理與信息工程學(xué)院，福建 福州 350116,；2.福州大學(xué) 計(jì)算機(jī)圖像圖形研究所,，福建 福州 350116）

　　摘要：虛擬手術(shù)系統(tǒng)研究是計(jì)算機(jī)圖形學(xué)的一個重要領(lǐng)域，為了提高肌肉纖維紋理合成的真實(shí)感與實(shí)時性,，文章采用了基于場向參數(shù)化的方法,，并結(jié)合最光滑方向場進(jìn)行了三維模型上的肌肉纖維紋理映射與合成，通過布置奇異點(diǎn),，模擬肌肉纖維損傷的狀態(tài),。該系統(tǒng)實(shí)現(xiàn)了場向參數(shù)化的可視化及肌肉纖維紋理合成的簡單交互，實(shí)驗(yàn)結(jié)果表明,，系統(tǒng)的實(shí)時性與真實(shí)感均得到提高,。

　　關(guān)鍵詞：虛擬手術(shù)；場向參數(shù)化,；最光滑方向場,；紋理合成

　　中圖分類號：TP391.41文獻(xiàn)標(biāo)識碼：ADOI： 10.19358/j.issn.1674-7720.2017.09.006

　　引用格式：馬健超，陳國棟,，周霆.基于場向參數(shù)化的肌肉纖維紋理合成研究［J］.微型機(jī)與應(yīng)用,，2017,36（9）：18-21.

0引言

　　隨著現(xiàn)代醫(yī)學(xué)技術(shù)和計(jì)算機(jī)技術(shù)的發(fā)展，借助計(jì)算機(jī)圖形技術(shù)分析處理醫(yī)學(xué)問題成為了醫(yī)學(xué)研究和計(jì)算機(jī)圖形技術(shù)的熱點(diǎn),，虛擬手術(shù)就是其中一個重要的學(xué)科發(fā)展方向,，其具有沉浸性、交互性等特點(diǎn)［1］,。

　　在計(jì)算機(jī)圖形學(xué)中,，紋理的應(yīng)用是增強(qiáng)真實(shí)感的有效方法，對于三維表面紋理合成,，實(shí)現(xiàn)的目標(biāo)是將二維紋理映射到三維表面,，并且不產(chǎn)生走樣和扭曲。現(xiàn)有方法通常是把表面領(lǐng)域通過參數(shù)化方法展平,，然后沿著表面局部坐標(biāo)系進(jìn)行采樣,，將采樣得到的平面領(lǐng)域與樣本紋理的領(lǐng)域進(jìn)行比較［2］。Praun［3］等人提出用重疊紋理技術(shù)來合成三維表面紋理,，該算法需要較多的人工干預(yù)；Wei［4］等人把表面紋理的顏色信息存儲在模型的頂點(diǎn)上,，根據(jù)松弛算法生成方向場來定義三維表面局部坐標(biāo)系,，但合成速度不理想,；Turk［5］等人使用密集模型保存豐富紋理細(xì)節(jié)，對每個目標(biāo)領(lǐng)域進(jìn)行局部參數(shù)化,，合成速度較慢,。這些方法都從圖像特征的統(tǒng)計(jì)相似性來解決問題，但不能很好地繪制出肌肉纖維紋理的特點(diǎn),。骨骼肌由肌腹和肌腱構(gòu)成,，肌腹由大量的橫紋纖維構(gòu)成，不同部位間纖維方向差異較大,，而肌腱由腱腱纖維構(gòu)成［6］,，肌肉損傷的表現(xiàn)為肌肉纖維沿筋膜面羽毛狀擴(kuò)展，或向鄰近肌肉擴(kuò)展［7］,。

　　為了提高虛擬手術(shù)中肌肉纖維仿真的真實(shí)感和實(shí)時性,，本文從幾何學(xué)的角度來看待這個問題，采用最光滑方向場與場向參數(shù)化相結(jié)合,，在Ray［8］等人的全局場面參數(shù)化方法的基礎(chǔ)上,，允許加入新的奇異點(diǎn)，以此來仿真肌肉損傷,，并省略了旋度校正和單位化約束,，使用一個簡單的凸二次能量來規(guī)劃問題，算法速度得到提升,，通過簡單的交互,，可以實(shí)時改變最光滑方向場的方向，從而得到三維模型上不同方向的肌肉纖維紋理,，可應(yīng)用到虛擬手術(shù)中,。

　　本文實(shí)現(xiàn)的整體算法流程如圖1所示，通過讀取三維網(wǎng)格模型,，如OBJ格式,，使用重新定義的狄利克雷能量來獲取最光滑方向場，使用該方向場進(jìn)行參數(shù)化,，得到相應(yīng)的紋理坐標(biāo),，最后使用模型加載庫Assimp及OpenGL等開源庫進(jìn)行紋理的合成。

1最光滑方向場

　　1.12-方向場

　　本文中的方向場指的是單位長度的矢量場,，方向場的度n指的是曲面上每一點(diǎn)有n等間隔分布的方向場,。如圖2所示，左圖為n為1時,，即傳統(tǒng)意義上的場;右圖為n為2時,，稱為2方向場［9］，每一點(diǎn)由兩個方向相反的單位矢量組成。這些方向場通常存在奇異點(diǎn),，即方向場在該點(diǎn)無法光滑地變化,，注意，本文產(chǎn)生的方向場將自動地布置奇異點(diǎn)的個數(shù)與位置,。

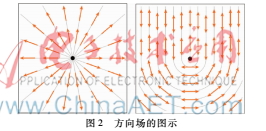
　　本文將曲面M上的一點(diǎn)的切空間視為復(fù)數(shù)域C的副本,，其上的切矢量可用復(fù)數(shù)乘以一個基矢量來表示，若以實(shí)軸為基矢量,，再通過平方,，得到一個不需要考慮單位約束的方向場的表示方法，為：

　　u=z2=ei2kπ,k=0,1(1)

　　1.2光滑能量

　　通過使用狄利克雷能量來測量2方向場ψ的光滑度［10］,，表示協(xié)變導(dǎo)數(shù),，也就是曲面上的列維奇維塔聯(lián)絡(luò)，表示為：

　　但方向場中,，在奇異點(diǎn)處該能量變得無限大,，導(dǎo)致該公式失去意義，而每一個2方向場可寫成一個比例因子與單位方向場的乘積,，即：

　　ψ=aφ(3)

　　將所有的ψ中最小的狄利克雷能量定義為2方向場的能量,，即式(4)，此時奇異點(diǎn)處的能量將變?yōu)榱?，從而解決了上述的問題,。

　　遍歷所有方向場，從而得到全局最小化的方向場,，也就是最光滑方向場,，由于經(jīng)過了縮放的2方向場的集合與2矢量場的集合是沒有區(qū)別的，所以可以替而求解,。

　　這意味著一個最小特征值的問題,，三維網(wǎng)格上所有方向場ψ都是分段線性的，將其表示為基底的復(fù)線性組合,，V代表點(diǎn)集,。

　　式(5)的問題轉(zhuǎn)化為求解特征向量的問題。等式(7)中,，A是一個相對于分段線性基底Ψi的埃爾米特矩陣,，M是埃爾米特質(zhì)量矩陣，使用逆冪迭代法來求解,，得出最光滑方向場,。

　　Au=λMu(7)

　　2場向參數(shù)化

　　2.1坐標(biāo)函數(shù)

　　首先需要選擇參數(shù)化后的坐標(biāo)函數(shù)的表達(dá)形式，Ray［8］等人和Zhang［11］等人提出使用復(fù)數(shù)域的矢量值函數(shù),，其角度分量提供最終的坐標(biāo),，但每一點(diǎn)有一個四階的懲罰項(xiàng)，導(dǎo)致了非凸規(guī)劃問題，所以本算法忽略了這一項(xiàng),，同樣使用一個復(fù)數(shù)域的矢量值函數(shù)ψ,，用其幅角α作為參數(shù)化后的坐標(biāo),，為：

　　α=argψ(8)

　　設(shè)定最光滑方向場為X,，每點(diǎn)的單位化函數(shù)為：

　　φ=eiα(9)

　　角α只沿著方向X以速率ν來變化，通過微分,，得到

　　dφ=iωφ(10)

　　這意味著通過求解該等式可以得到角速度ω,，但需要方向場總是可積的，因此考慮它的L2殘差：

　　其中算子c=d－iω恰好是曲面M上的一個聯(lián)絡(luò),，ε可以被認(rèn)為是在一個復(fù)變函數(shù)上的狄利克雷能量,，所以定義單位化函數(shù)φ能量為比例函數(shù)a下，所有可能的最小的狄利克雷能量：

　　在單位化函數(shù)φ上的能量極小化是等價于在所有復(fù)變函數(shù)ψ上的狄利克雷能量極小化：

　　因此對應(yīng)為一個標(biāo)準(zhǔn)的求解特征值的問題,，ψ為特征函數(shù),，Δs為薛定諤算子。

　　Δsψ=λψ(14)

　　2.2不可定向特征

　　方向場中存在不可定向的點(diǎn),，即在奇異點(diǎn)有不可定向的特征,，引進(jìn)Kalberer［12］等人提出的二次覆蓋的概念。除了奇異點(diǎn)之外,，二次覆蓋看起來就像原曲面的副本,，但算法中并沒有實(shí)際地去構(gòu)造二次覆蓋，只是用這一思想來解決奇異點(diǎn)的問題,。圖3為二次覆蓋于原曲面的示意圖,，MD為二次覆蓋，M為原曲面,，τ稱為片交換函數(shù),，ρ將二次覆蓋映射回原曲面，曲面M上的線場,，在MD上任意選擇其中一個方向的場,。

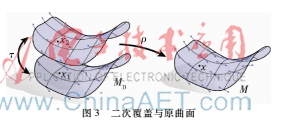
　　2.3離散化

　　三角網(wǎng)格上，每一個頂點(diǎn)i∈V,，用單位切矢量Xi和目標(biāo)線頻率νi∈R+共同定義了矢量Zi=νiXi,，離散化算法的具體步驟如下：

　　輸入：二維單純復(fù)形K（三角網(wǎng)格）。

　　過程：

　?。?）將Z投影到每一條邊上,，得到角位移ω；

　?。?）構(gòu)建類拉普拉斯矩陣A,，元素由ω決定；

　　（3）求矩陣A最小特征值對應(yīng)特征向量ψ ,。

　　輸出：每一個面上,，通過ψ和ω得到計(jì)算紋理坐標(biāo)α。

　　首先求得角位移ωij,，即邊矢量與輸入矢量場的內(nèi)積

　　的平均值,。

　　ωij=∫ijω=12(〈eij,Zi〉+〈eij,Zj〉)(15)

　　然后每個三角形構(gòu)建類余切拉普拉斯矩陣，即薛定諤算子的離散化,。該矩陣A是正定對稱,，與余切拉普拉斯矩陣有相同結(jié)構(gòu)，對于每個正則邊ij∈E,，非對角塊為：

　　Aij=－wij［eiωij］,sij=－1

　?。瓀ij［eiωij］,sij=+1

　　Aji=ATij(16)

　　矩陣A的對角塊為：

　　Aii=∑ij∈E［ωij］(17)

　　塊對角集總質(zhì)量矩陣為B，用Aijk表示三角形ijk的面積,，對角元素為關(guān)聯(lián)三角形總面積的三分之一,。

　　Bii=13∑ijk∈FAijk(18)

　　存在ψi=ai+bii的某個值來使ε最小，用ai,bi∈R值交替組成的一個矢量x,，通過求解式(19)的最小特征值對應(yīng)的特征向量x,，使用喬里斯基分解矩陣A，然后應(yīng)用逆冪法來求解,。

　　Ax=λBx(19)

　　求得ψ后,，如果僅通過式(8)來求最終的坐標(biāo)函數(shù)α，將產(chǎn)生畸變與扭曲,，因此采用旋轉(zhuǎn)形式進(jìn)行調(diào)整,，最終坐標(biāo)為：

　　αjki:=arg(ψi)

　　αkij:=arg(ψi)+σij

　　αijk:=arg(ψi)+σik(20)

3結(jié)果與分析

　　3.1編程環(huán)境與開源庫

　　本課題使用系統(tǒng)為Window 7，編程環(huán)境為VS2012,，處理器為2.40 GHz,，內(nèi)存8 GB，顯卡為AMD Radeon 6550M,。采用了開源庫SuiteSparse來實(shí)現(xiàn)對稀疏矩陣的運(yùn)算,，選用了模型加載庫Assimp，選用的三維模型格式是OBJ格式,，還有OpenGL及其擴(kuò)展庫GLUT和GLEW處理窗口的創(chuàng)建,、基本的交互，使用著色語言GLSL編寫了頂點(diǎn)著色器和片段著色器,。

　　3.2紋理合成結(jié)果與分析

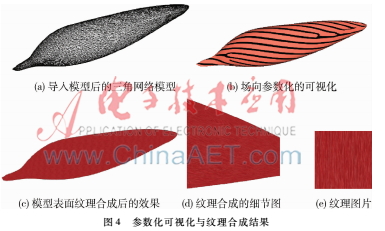
　　圖4展示了整個紋理合成的過程,，使用模型的面片數(shù)為6 142片，（a）為導(dǎo)入模型后顯示的三角網(wǎng)格模型,；（b）為場向參數(shù)化的可視化,，可看到奇異點(diǎn)（分叉點(diǎn)）,；（c）為模型表面紋理合成后的效果；（d）為紋理合成的細(xì)節(jié)圖,，可以看到紋理的方向與方向場一致,；（e） 為所使用的紋理圖片。圖5為圖4的2方向場經(jīng)過旋轉(zhuǎn)90°后的可視化結(jié)果,，從右圖可以看到肌肉纖維紋理的方向已經(jīng)發(fā)生了改變,，但是同樣與方向場方向保持一致。

　　圖6展示的是參數(shù)化中奇異點(diǎn)與紋理合成后細(xì)節(jié)的對比,，使用的模型的面片數(shù)為15 418片,，可以看到紋理在奇異點(diǎn)處發(fā)生了分叉，但總體還是保持連續(xù)的,，以此來模擬肌肉的輕微損傷，左圖為場向參數(shù)化的可視化,，右圖為奇異點(diǎn)處的紋理細(xì)節(jié),。

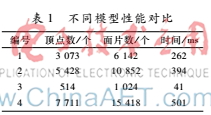
　　通過對不同面片數(shù)的模型進(jìn)行實(shí)驗(yàn)，得到了以下的對比數(shù)據(jù),，表1表明了面片數(shù)從1 K~16 K的幾種情況下,，紋理合成所需要的時間基本控制在0.5 s以內(nèi)，這樣的性能是符合進(jìn)行實(shí)時操作和交互的,。表2通過與其他算法的對比,，列出了部分?jǐn)?shù)據(jù)，表明了本文所使用的算法性能得到提升,，計(jì)算所需時間平均縮短為算法1的35.2%,。

4結(jié)論

　　本文基于場向參數(shù)化的方法，結(jié)合了最光滑方向場,，并使用了一系列開源庫,，實(shí)現(xiàn)了對肌肉纖維紋理的合成，最終的系統(tǒng)能夠?qū)崿F(xiàn)實(shí)時操作與交互,，在保證真實(shí)感的同時,，也證明了所使用算法的性能有較大的提高，為虛擬手術(shù)中肌肉手術(shù)的場景的進(jìn)一步研究提供了條件,。

　　參考文獻(xiàn)

　?。?］ 邢英杰, 張少華, 劉曉冰. 虛擬手術(shù)系統(tǒng)技術(shù)現(xiàn)狀［J］. 計(jì)算機(jī)工程與應(yīng)用, 2004, 40(7):88-90.

　　［2］ 韓建偉. 基于樣本的三維表面紋理快速合成技術(shù)［D］. 杭州：浙江大學(xué), 2009.

　?。?］ PRAUN E,FINKELSTEIN A,HOPPE H. Lapped textures［C］. Proceeding of ACM SIGGRAPH 2000.New York,USA:ACM Press/AddisonWelsey Publishing Co.2000:465-470.

　?。?］ WEI L,LEVOY M. Texture synthesis over arbitrary manifold surfaces［C］.Proceedings of ACM SIGGRAPH 2001.New York,USA:ACM,2001:355-360.

　　［5］ TURK G. Texture synthesis on surfaces［C］. Proceedings of ACM SIGGRAPH 2001.NY, ACM,2001:347-354.

　?。?］ 席占國, 喬亞亞, 沈素紅. 超聲診斷肌肉損傷的臨床價值［J］. 醫(yī)藥前沿, 2014(18):206207.

　?。?］ 劉亞娟, 冉艮龍, 葉倫,等. 大腿肌肉損傷的MRI診斷［J］. 西南國防醫(yī)藥, 2015, 25(11):1222-1224.

　?。?］ RAY N. Periodic global parameterization［J］. Acm Transactions on Graphics, 2006, 25(4):1460-1485.

　　［9］ VAXMAN A, CAMPEN M, DIAMANTI O, et al. Directional field synthesis, design, and processing［C］． SIGGRAPH Asia,， 2016:1-30.

　?。?0］ LIU B B, WENG Y L, WANG J N, et al. Orientation field guided texture synthesis［J］. Journal of Computer Science and Technology, 2013, 28(5):827-835.

　　［11］ ZHANG M, HUANG J, LIU X, et al. A wavebased anisotropic quadrangulation method［J］. Acm Transactions on Graphics, 2010, 29(4):157-166.

　?。?2］ KLBERER F, NIESER M, POLTHIER K. Stripe Parameterization of Tubular Surfaces［M］. Topological Methods in Data Analysis and Visualization, 2010.