0 引言

    電力電子設(shè)備作為電力系統(tǒng)的關(guān)鍵部件,，通常表現(xiàn)為連續(xù)性和離散型相互作用的混雜特性,，對電力系統(tǒng)的可靠性具有重要影響^[1]。電力電子裝置結(jié)構(gòu)日漸復(fù)雜,，其故障類型也越來越多,，為確保電力電子裝置安全、可靠,、高效地運行,，對其進行故障診斷研究并提高故障診斷準確率至關(guān)重要。

    現(xiàn)階段故障診斷方法主要分為基于數(shù)據(jù)驅(qū)動和基于模型的故障診斷方法,，前者需要大量的歷史數(shù)據(jù)作為先驗知識,，后者需要建立系統(tǒng)的準確物理模型^[2]。而在基于模型的故障診斷中,，往往沒有考慮系統(tǒng)的參數(shù)不確定性,，容易造成誤報警。為解決這一問題,，Armengol J等運用區(qū)間算法研究故障檢測與診斷^[3],。Henry和Zolghari提出線性分式變換不確定性模型的濾波器方法進行殘差生成和估計^[4]。Ilyas Rahal M等人建立線性分式變換的混雜鍵合圖模型進行魯棒故障檢測與隔離^[5],。

    本文針對混雜系統(tǒng)的參數(shù)不確定性,，提出運用BG-LFT建立系統(tǒng)參數(shù)不確定性DHBG模型,，通過DHBG產(chǎn)生魯棒殘差和自適應(yīng)閾值，以減少故障診斷的誤報率,。通過仿真來驗證所提出方法在逆變器魯棒故障診斷中的有效性,。

1 基于鍵合圖的系統(tǒng)不確定性建模

1.1 線性分式變換形式

    線性分式變換(Linear Fractional Transformation，LFT)由Redheffer學(xué)者于1960年提出^[6],，在多變量不確定系統(tǒng)的魯棒控制合成領(lǐng)域得到廣泛應(yīng)用,。具有把系統(tǒng)解耦成確定部分和不確定部分的優(yōu)點，是解決結(jié)構(gòu)奇異值問題的有力工具^[7],，為構(gòu)造系統(tǒng)的參數(shù)不確定模型提供了有效的途徑,。模型的LFT結(jié)構(gòu)圖如圖1所示。確定部分用增廣矩陣M表示,，矩陣Δ表示所有的不確定性部分（結(jié)構(gòu)的,、非結(jié)構(gòu)的參數(shù)或建模不確定、測量噪音等）,。w和z分別表示系統(tǒng)的輔助輸入和輔助輸出,；u和y分別表示系統(tǒng)的真實輸入和真實輸出。

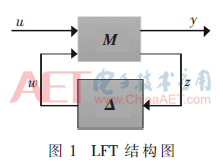
1.2 參數(shù)不確定性的鍵合圖建模

    運用鍵合圖理論進行參數(shù)不確定性魯棒故障診斷,，通過建立系統(tǒng)的診斷鍵合圖模型,，可將解析冗余關(guān)系(Analytical Redundancy Relation，ARR)解耦為確定部分ARR_n=f(SSe,，SSf,，Se，Sf,，MSe,，MSf，u,，θ_n)和不確定部分bn=f(SSe,，SSF，δ_θθ_n),。其中,，一個ARR表示為依賴系統(tǒng)參數(shù)(θ)的約束，SSe和SSf是檢測器對偶化后的測量,，(Se,，Sf,，MSe,，MSf，u)分別表示已知輸入,，θ_n是標(biāo)稱參數(shù),，δ_θ是參數(shù)的不確定性,。ARR的確定部分計算殘差，不確定部分計算實時閾值,。

    參數(shù)的不確定性δ_θ可表示為加性或乘性形式,，如式(1)：

    其中Δ_θ和δ_θ=(Δ_θ)/θ_n分別表示為相對于參數(shù)θ_n標(biāo)稱值的絕對偏差和相對偏差。

    阻抗性R元件的乘性不確定性如圖2,。

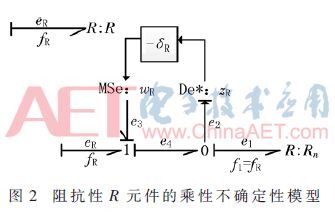
    阻抗型R元件的不確定性表示如下：

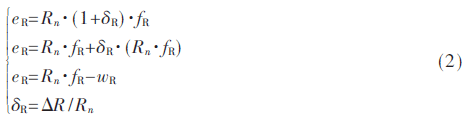
    其中R_n,、δ_R、ΔR,、e_R,、f_R分別表示R元件的標(biāo)稱值、乘性不確定性,、加性不確定性,、勢和流。w_R表示加入?yún)?shù)不確定性后勢的虛擬輸入,。

    鍵合圖模型中的“-”表示半定向箭頭的源指向相應(yīng)的結(jié)點,。符號De^*和Df^*是虛擬傳感器。其他元件的乘性不確定性參照阻抗性R元件,。

2 魯棒解析冗余關(guān)系和殘差估計

    通過以下3個步驟得到系統(tǒng)的魯棒ARR：

    (1)為避免模型的未知初始條件,，鍵合圖模型優(yōu)先分配微分因果關(guān)系。

    (2)基于覆蓋因果路徑,，0和1結(jié)點至少包含一個傳感器,。可推導(dǎo)ARR方程如下：

3 參數(shù)性故障診斷實例仿真

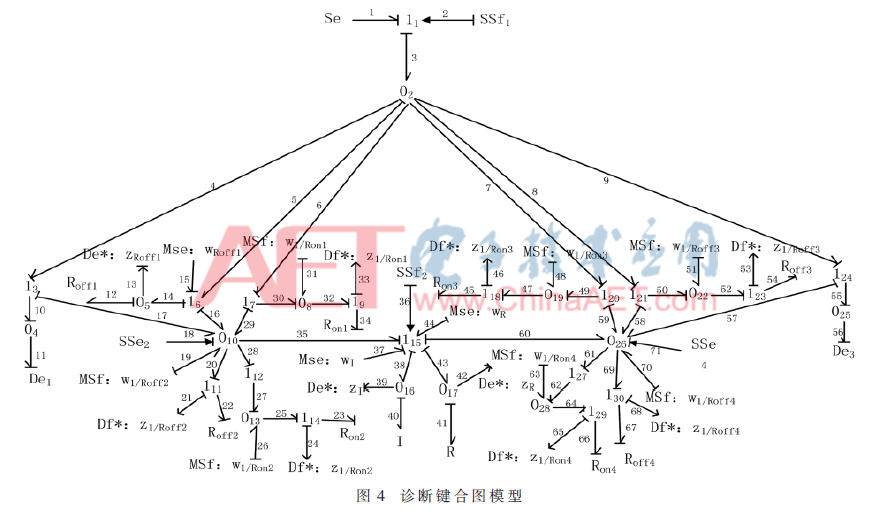
3.1 診斷鍵合圖模型

    單相全橋逆變器共有2個橋臂,，可以看成由兩個半橋電路組合而成,。把V1和V4作為一對，V2和V3作為一對,，成對的兩個IGBT同時導(dǎo)通,，兩對IGBT交替導(dǎo)通180°，結(jié)構(gòu)如圖3所示,。

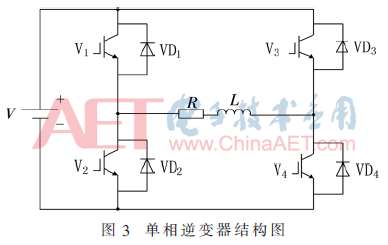
    對單相全橋逆變器進行故障診斷,，需建立其對應(yīng)的診斷鍵合圖模型。因此,，通過引入虛擬勢（流）傳感器將鍵合圖模型中的電壓（電流）作為輸入,，且在診斷模型中需盡可能地將傳感器進行對偶化處理^[9]。而有些傳感器不能產(chǎn)生解析冗余關(guān)系,，不需要將其對偶化^[10],。根據(jù)上述分析，為系統(tǒng)重新分配因果關(guān)系，建立單相全橋逆變器的故障診斷鍵合圖模型,，如圖4所示,。

3.2 魯棒解析冗余關(guān)系

    根據(jù)圖4所示的診斷鍵合圖模型，從而可得到魯棒ARR分別的兩個分離部分：

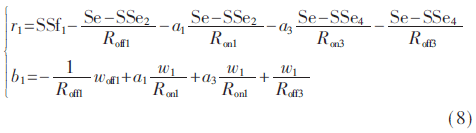
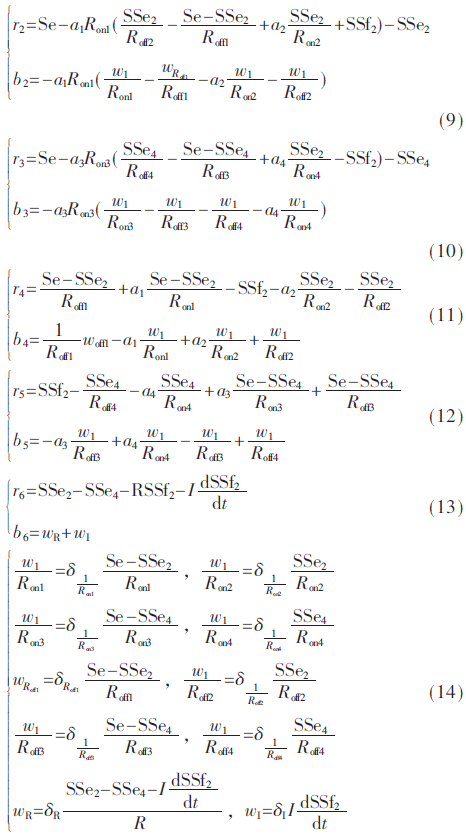
    其中,，Se是已知輸入,，SSe_i和SSf_i是檢測器對偶化后的測量，w_1/Roni,、w_1/Roffi和w_Roffi是各元件參數(shù)所對應(yīng)的虛擬輸入,，δ_Roffi、δ_1/Roffi和δ_1/Roni是各元件參數(shù)的乘性不確定性,。

3.3 仿真結(jié)果

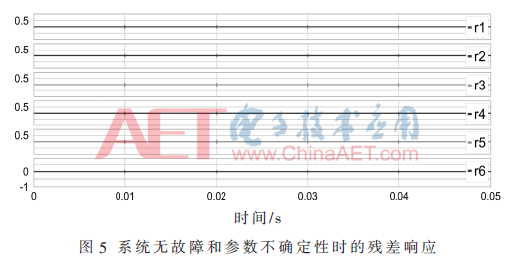
    當(dāng)系統(tǒng)無故障時,，殘差的值近似等于零或者處于小幅度的波動狀態(tài)但不超過閾值的上下界限。若系統(tǒng)中對故障敏感的殘差明顯偏離零值甚至超過閾值的范圍,，則認為系統(tǒng)中有故障發(fā)生并給以報告,。如果殘差在(-δ_θ，δ_θ)范圍內(nèi),，由元器件參數(shù)不確定性對系統(tǒng)或者殘差造成影響不應(yīng)該造成報警,，此時不認為系統(tǒng)或者元器件發(fā)生了故障。

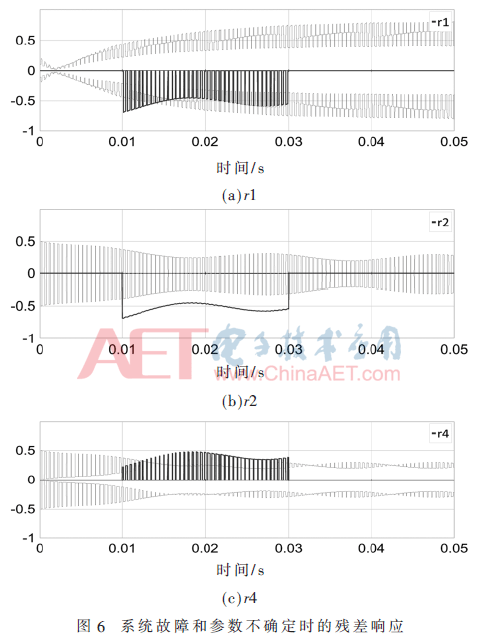
    在仿真中,，參數(shù)的不確定性系數(shù)δ_θ為0.05,。仿真結(jié)果如圖5和圖6所示。圖5表示在系統(tǒng)無故障和所有參數(shù)不確定時,，殘差全為0,。如果殘差超過閾值，則系統(tǒng)故障,。引入元件R_on1參數(shù)性故障,，分析解析冗余關(guān)系可知殘差r₁、r₂和r₄對此故障敏感,，從圖6可看出,，殘差r₁、r₂和r₄明顯超過自適應(yīng)閾值范圍,，觸發(fā)故障警報,，R_on1故障被有效地檢測出。

4 結(jié)論

    本文針對混雜系統(tǒng)中存在參數(shù)不確定性,，傳統(tǒng)的故障診斷方法無法減少誤報警的問題,，提出運用BG-LFT建立系統(tǒng)參數(shù)不確定DHBG模型，結(jié)合自適應(yīng)閾值評價殘差,，對系統(tǒng)進行魯棒故障診斷,，能準確檢測出系統(tǒng)故障,，有效降低誤報率，并在單相全橋逆變器中得到了驗證,，實驗結(jié)果表明該方法是有效的,。

參考文獻

[1] 王文輝,，劉帥,，周東華.混雜系統(tǒng)故障診斷方法綜述[J].系統(tǒng)工程與電子技術(shù)，2006,，28(12)：1853-1857.

[2] 趙文浩,，閻威武.基于數(shù)據(jù)驅(qū)動的故障診斷研究[J].微計算機信息，2010(28)：104-106.

[3] ARMENGOL J,，TRAVE-MASSUYES L,，VEHI J，et al.A survey on interval model simulators and their properties related to fault detection[J].Annual reviews in control,，2000,，24:：31-39.

[4] HENRY D，ZOLGHADRI A.Norm-based design of robust FDI schemes for uncertain systems under feedback control: Comparison of two approaches[J].Control engineering practice,，2006,，14(9)：1081-1097.

[5] RAHAL M I，OULD B B,，MEGHEBBAR A.Hybrid bond graph model based for robust fault detection and isolation[J].Proceedings of the Institution of Mechanical Engineers,，Part I：Journal of Systems and Control Engineering，2016,，230(2)：145-163.

[6] REDHEFFER R M.On a certain linear fractional transformation[J].Studies in Applied Mathematics,，1960，39(1-4)：269-286.

[7] KAM C S,，Dauphin-Tanguy G.Bond graph models of structured parameter uncertainties[J].Journal of the Franklin Institute,，2005，342(4)：379-399.

[8] ROTSHTEIN A P,，POSNER M,，RAKYTYANSKA H B.Cause and effect analysis by fuzzy relational equations and a genetic algorithm[J].Reliability Engineering & System Safety，2006,，91(9)：1095-1101.

[9] TOUATI Y,，MERZOUKI R，BOUAMAMA B O.Robust diagnosis to measurement ucertainties using bond graph approach：application to intelligent autonomous vehicle[J].Mechatronics,，2012,，22(8)：1148-1160.

[10] BORUTZKY W.Bond graphs for modelling, control and fault diagnosis of engineering systems[M].Springer，2017.

作者信息:

彭冬梅,，帕孜來·馬合木提

(新疆大學(xué) 電氣工程學(xué)院,，新疆 烏魯木齊830047)