《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 通信與網(wǎng)絡(luò) > 設(shè)計(jì)應(yīng)用 > 電力通信大數(shù)據(jù)并行化聚類算法研究
電力通信大數(shù)據(jù)并行化聚類算法研究
2018年電子技術(shù)應(yīng)用第5期
曾 瑛,，李星南,，劉新展
廣東電網(wǎng)公司 廣東電網(wǎng)電力調(diào)度控制中心，廣東 廣州510600
摘要： 隨著電力通信技術(shù)的發(fā)展,，產(chǎn)生了大量分布式電力通信子系統(tǒng)以及海量電力通信數(shù)據(jù),，在海量數(shù)據(jù)中挖掘重要信息變得十分重要,。聚類分析作為數(shù)據(jù)并行化處理和信息挖掘的一個有效手段，在電力通信中得到了廣泛的應(yīng)用,。然而,，傳統(tǒng)聚類算法在處理海量電力數(shù)據(jù)時已不能滿足時間性能的要求。針對這一問題,，提出了一種基于MapReduce模型的并行化k-medoids聚類算法,，首先采用基于密度的聚類思想對k-medoids算法初始點(diǎn)的選取策略進(jìn)行優(yōu)化，并利用Hadoop平臺下的MapReduce編程框架實(shí)現(xiàn)了算法的并行化處理,。實(shí)驗(yàn)結(jié)果表明，改進(jìn)的并行化聚類算法與其他算法相比,，減少了聚類時間,，提高了聚類精度，有利于對電力數(shù)據(jù)的有效分析和利用,。
中圖分類號： TP181
文獻(xiàn)標(biāo)識碼： A
DOI：10.16157/j.issn.0258-7998.180780
中文引用格式： 曾瑛,，李星南，劉新展. 電力通信大數(shù)據(jù)并行化聚類算法研究[J].電子技術(shù)應(yīng)用,，2018,，44(5)：1-4，24.
英文引用格式： Zeng Ying,，Li Xingnan,，Liu Xinzhan. Research on parallelization clustering algorithm for power communication[J].Application of Electronic Technique，2018，44(5)：1-4,，24.
Research on parallelization clustering algorithm for power communication big data
Zeng Ying,，Li Xingnan，Liu Xinzhan
Power Dispatching Control Center,，Guangdong Grid Corporation,，Guangzhou 510600，China
Abstract： With the development of power communication technology, a large number of distributed power communication subsystems and massive power communication data have been generated. It is important to mine important information in the vast amounts of data. Cluster analysis, as an effective means of data processing and information mining, has been widely used in power communication. However, the traditional clustering algorithms can not meet the time performance requirements when dealing with massive power data. To solve this problem, a parallel k-medoids clustering algorithm based on MapReduce model is proposed to support the effective analysis and utilization of power data. The algorithm uses density-based clustering method to optimize the selection strategy of k-medoids initial point, and implements the algorithm parallelization using MapReduce programming framework under Hadoop platform. Experimental results show that compared with other algorithms, the improved parallel algorithm reduces the clustering time and improves the clustering accuracy.
Key words : power communication,；clustering,；parallelism；optimization

0 引言

    隨著電力通信網(wǎng)絡(luò)以功能為中心持續(xù)性發(fā)展,，產(chǎn)生了大量分專業(yè),、分功能和分管理域的運(yùn)維管理系統(tǒng)，進(jìn)而導(dǎo)致大量電力數(shù)據(jù)孤島的產(chǎn)生,。如何利用分布式系統(tǒng)更好地處理這些數(shù)據(jù)量巨大且類型復(fù)雜的電力通信運(yùn)維數(shù)據(jù)已成為研究的熱點(diǎn)問題,。聚類分析作為數(shù)據(jù)處理的一個有效手段，支持對大量無序分散數(shù)據(jù)進(jìn)行整合分類從而進(jìn)行更深層次的關(guān)聯(lián)性分析或者數(shù)據(jù)挖掘,，在電力通信網(wǎng)絡(luò)中得到越來越廣泛的應(yīng)用,。同時，分布式系統(tǒng)中并行化處理機(jī)制因其優(yōu)秀的靈活性和高效性逐漸成為數(shù)據(jù)挖掘的一個重要研究方向,。

    國內(nèi)外學(xué)者也越來越對這方面加大關(guān)注,，文獻(xiàn)[1]提出了一種基于DBSACN算法的并行優(yōu)化的聚類算法。文獻(xiàn)[2]中通過計(jì)算距離選擇最中心的k個數(shù)據(jù)點(diǎn)作為初始聚類中心,，然后用k-medoids算法進(jìn)行迭代聚類,，提高了聚類效果，但不適合處理大規(guī)模數(shù)據(jù),；文獻(xiàn)[3]提出了一種蟻群 k-medoids 融合聚類算法,，該算法不需要人為確定類簇數(shù)目和初始聚類中心，提高了聚類效果,，但也僅只適用于小型數(shù)據(jù)集,；文獻(xiàn)[4]采用基于粒計(jì)算的聚類算法，該算法在初始聚類中心的選取過程中的計(jì)算量較大,，且在處理大規(guī)模數(shù)據(jù)時存在時延問題,；文獻(xiàn)[5]提出了將局部搜索過程嵌入到迭代局部搜索過程中的方法，顯著減少了計(jì)算時間,。文獻(xiàn)[6]在Hadoop平臺上實(shí)現(xiàn)了傳統(tǒng)k-medoids聚類算法的并行化處理,，減少了聚類時間，但在初始聚類中心的選取機(jī)制上沒有進(jìn)行改進(jìn),，沒有提高聚類效果,；文獻(xiàn)[7]采用基于核的自適應(yīng)聚類算法,，克服了k-medoids 的初值敏感問題，但是沒有降低算法的時間復(fù)雜度,。

    綜上所述,，k-medoids聚類算法存在初始值敏感、運(yùn)行速度慢,、時間復(fù)雜度較高等問題,，需要對k-medoids算法中初始點(diǎn)選取以及并行化方式進(jìn)行算法優(yōu)化設(shè)計(jì)。

1 k-medoids聚類初始點(diǎn)選取改進(jìn)機(jī)制

    k-medoids算法是一種基于劃分的聚類算法,，具有簡單,、收斂速度快以及對噪聲點(diǎn)不敏感等優(yōu)點(diǎn)，因此在模式識別,、數(shù)據(jù)挖掘等領(lǐng)域都得到了廣泛的應(yīng)用,。k-medoids算法初始中心點(diǎn)的選取十分重要，如果初始中心點(diǎn)選擇的是離群點(diǎn)時,，就會導(dǎo)致由離群點(diǎn)算出的質(zhì)心會偏離整個簇,，造成數(shù)據(jù)分析不正確；如果選擇的初始中心點(diǎn)離得太近,，就會顯著增加計(jì)算的時間消耗,。因此本文算法首先對初始中心點(diǎn)的選取進(jìn)行優(yōu)化?；诿芏鹊木垲惪梢院芎玫胤蛛x簇和環(huán)境噪聲,，所以本文采用基于密度的聚類思想，盡量減少噪聲數(shù)據(jù)對選取初始點(diǎn)的影響,。

    定義1：點(diǎn)密度是對于數(shù)據(jù)集U中的數(shù)據(jù)集的樣本點(diǎn)x,，以x為球心，某一正數(shù)r為半徑的球形域中所包含樣本點(diǎn)的個數(shù),，記作Dens(x),。其中：

wlw1-gs1-4.gif

    本文算法中，首先對每個數(shù)據(jù)點(diǎn)并行計(jì)算點(diǎn)密度,，并將點(diǎn)密度作為該數(shù)據(jù)點(diǎn)的一個屬性,。選取初始聚類中心的具體步驟如下：

    (1)計(jì)算數(shù)據(jù)集中m個數(shù)據(jù)點(diǎn)之間的距離。

    (2)計(jì)算每個樣本點(diǎn)的點(diǎn)密度Dens(xi)以及均值點(diǎn)密度AvgDens,，將點(diǎn)密度大于AvgDens的點(diǎn)即核心點(diǎn)存入集合T中，并記錄其簇中所包含的數(shù)據(jù)點(diǎn),。

    (3)合并所有具有公共核心點(diǎn)的簇,。

    (4)計(jì)算各個簇的類簇密度CDens(ci)，選擇其中k個較大密度的簇,，計(jì)算其中心點(diǎn),，即為初始聚類中心,。

    類簇中心點(diǎn)的計(jì)算方法如下：假設(shè)有一個類簇ci包含m個數(shù)據(jù)點(diǎn){x1，x2,，…,，xm}，則其中心點(diǎn)ni按如式(5)計(jì)算：

    wlw1-gs5-6.gif

    經(jīng)過上述步驟,，可以優(yōu)化初始聚類中心點(diǎn)的選取,，使之后的聚類迭代運(yùn)算更加有效，降低搜索范圍,，大大減少搜索指派的時間,。

2 k-medoids聚類算法并行化設(shè)計(jì)策略

    本文針對k-medoids算法具有初始點(diǎn)選取復(fù)雜、聚類迭代時間久,、中心點(diǎn)選取消耗資源過多等缺點(diǎn),，使用Hadoop平臺下的MapReduce編程框架對算法進(jìn)行初始點(diǎn)的點(diǎn)密度計(jì)算選取并行化、非中心點(diǎn)分配并行化和中心點(diǎn)更新并行化等方面的改進(jìn),。MapReduce分為Map(映射)和Reduce(化簡)兩部分操作,，使用MapReduce實(shí)現(xiàn)算法并行化關(guān)鍵在于Map函數(shù)和Reduce函數(shù)的設(shè)計(jì)。其中Map函數(shù)將可并行執(zhí)行的多個任務(wù)映射到多個計(jì)算節(jié)點(diǎn),，多個計(jì)算節(jié)點(diǎn)對各自被分派的任務(wù)并行進(jìn)行處理,，Reduce函數(shù)則是在各計(jì)算節(jié)點(diǎn)處理結(jié)束后，將計(jì)算結(jié)果返回給主進(jìn)程進(jìn)行匯總,。

2.1 點(diǎn)密度計(jì)算并行化策略

    在點(diǎn)密度的計(jì)算中,，由于一個數(shù)據(jù)點(diǎn)的點(diǎn)密度對其他數(shù)據(jù)點(diǎn)的點(diǎn)密度沒有影響，所以該計(jì)算過程是可以并行化的,。使用MultithreadedMapper在一個JVM進(jìn)程里以多線程的方式同時運(yùn)行多個Mapper,，每個線程實(shí)例化一個Mapper對象，各個線程并發(fā)執(zhí)行,。主進(jìn)程把數(shù)據(jù)點(diǎn)分派給若干個不同的計(jì)算節(jié)點(diǎn)進(jìn)行處理,，計(jì)算節(jié)點(diǎn)將數(shù)據(jù)平均分成k份，且有k個線程,，每個線程中的數(shù)據(jù)點(diǎn)都與數(shù)據(jù)集中所有點(diǎn)進(jìn)行距離計(jì)算,，進(jìn)而計(jì)算出點(diǎn)密度，最后通過Reduce函數(shù)將計(jì)算結(jié)果匯總并輸出,。并行處理使得點(diǎn)密度計(jì)算所用時間大大減少,，提高了算法的執(zhí)行效率。

2.2 非中心點(diǎn)分配及中心點(diǎn)更新并行化策略

    非中心點(diǎn)分配階段的主要工作是計(jì)算各數(shù)據(jù)點(diǎn)到每個中心點(diǎn)的距離,，由于每個數(shù)據(jù)點(diǎn)跟各個中心點(diǎn)距離的計(jì)算互不影響,，所以該計(jì)算過程也是可并行化的。此階段的MapReduce化過程中,，Map函數(shù)主要負(fù)責(zé)將數(shù)據(jù)集里除中心點(diǎn)外的每一個樣本點(diǎn)分配給與其距離最近的聚類中心,，Reduce函數(shù)則負(fù)責(zé)通過計(jì)算更新每一個簇的中心點(diǎn),，按照這個原則迭代下去一直到達(dá)到設(shè)定閾值。主進(jìn)程利用Map函數(shù)把非中心點(diǎn)分配的任務(wù)分派給若干個計(jì)算節(jié)點(diǎn),，每個計(jì)算節(jié)點(diǎn)采用基于Round-Robin的并行化分配策略,。首先把每一個數(shù)據(jù)點(diǎn)看作一個請求，輪詢地分配給不同的線程,，對非中心點(diǎn)和每一個中心點(diǎn)的距離進(jìn)行計(jì)算,，找出最小的距離，然后把該非中心點(diǎn)指派給最小距離所對應(yīng)的中心點(diǎn),。

    因?yàn)檩喸冋{(diào)度算法是假設(shè)所有服務(wù)器中的處理性能都是相同,，并不關(guān)心每臺服務(wù)器當(dāng)前的計(jì)算速度和響應(yīng)速度。因此當(dāng)用戶發(fā)出請求時,，如果服務(wù)間隔的時間變化較大的時候,，那么Round-Robin調(diào)度算法是非常容易導(dǎo)致服務(wù)器之間的負(fù)載發(fā)生不平衡表現(xiàn)。而本文中所運(yùn)用的每個數(shù)據(jù)點(diǎn)都是平等的,，所以不會造成服務(wù)器分配任務(wù)不均的問題,。因此基于Round-Robin的策略是可行的。

    本文算法在實(shí)現(xiàn)聚類的過程中經(jīng)歷了兩次并行化劃分,，分別是非中心點(diǎn)分配和中心點(diǎn)更新過程,。這兩次并行化過程是周而復(fù)始的，直到滿足程序退出的條件才會終止循環(huán),。

3 仿真實(shí)驗(yàn)與結(jié)果分析

    仿真實(shí)驗(yàn)分別使用本文算法,、DBSCAN并行化算法[1]和k-medoids并行化算法[8]進(jìn)行對比試驗(yàn)，證明各個算法的優(yōu)劣性,。為了證明本文算法的有效性,，實(shí)驗(yàn)將分析不同算法的聚類時間、聚類準(zhǔn)確度以及增加線程數(shù)之后的時間消耗,。實(shí)驗(yàn)將在兩種類型的數(shù)據(jù)集上進(jìn)行測試：

    (1)電力數(shù)據(jù)集,。電力通信數(shù)據(jù)的屬性有設(shè)備狀態(tài)、設(shè)備資產(chǎn),、網(wǎng)絡(luò)拓?fù)涞?，其?shù)據(jù)量約為1 GB。

    (2)公有數(shù)據(jù)集,。分別為200數(shù)量級的Northix,、1 000數(shù)量級的DSA、5 000數(shù)量級的SSC和10 000數(shù)量級的GPSS,。

3.1 電力數(shù)據(jù)集實(shí)驗(yàn)結(jié)果分析

    實(shí)驗(yàn)首先設(shè)置6個線程對數(shù)據(jù)集進(jìn)行處理,，三種算法對電力數(shù)據(jù)進(jìn)行聚類的結(jié)果見表1。其中k-medoids并行化算法[8]采用標(biāo)簽共現(xiàn)原則對初始點(diǎn)選取進(jìn)行改進(jìn),，但沒有考慮線程的分配方式,，因此其執(zhí)行效率最差；DBSCAN算法考慮到了初始點(diǎn)的選取,，并采用動態(tài)分配策略實(shí)現(xiàn)并行化,，但在計(jì)算動態(tài)分配過程中增加了一定消耗，因此聚類準(zhǔn)確度和執(zhí)行效率都略有提升,；本文所提出的算法,，既考慮了初始點(diǎn)的合理選取，同時采用簡單有效的并行化分配策略,，以減少計(jì)算和過多資源占用,，因此相對于k-medoids并行化算法和DBSCAN并行化算法執(zhí)行效率大幅提升，準(zhǔn)確度也有所提高,。

wlw1-b1.gif

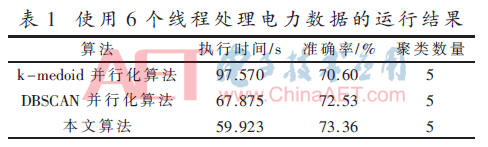
    然后增加線程處理器的數(shù)量至8個,，得到下表的聚類結(jié)果，見表2,。

wlw1-b2.gif

    由表2可得,，使用8個線程時，本文算法比k-medoids并行化算法執(zhí)行時間快了42.64%,，比DBSCAN并行化算法快了24.70%,。

    各類算法增加線程后所用時間相比原算法減少的百分比如圖1。

wlw1-t1.gif

    由圖1可知,，k-medoids并行化算法減少了10.20%,，DBSCAN并行化算法減少了1.68%，本文算法減少了16.13%,，說明本文算法在線程數(shù)增加時,，可以更有效地減少運(yùn)算時間，提高執(zhí)行效率,。

3.2 公有數(shù)據(jù)集實(shí)驗(yàn)結(jié)果分析

    基于Northix,、DSA、SSC和GPSS數(shù)據(jù)集使用5個線程實(shí)現(xiàn)算法的聚類準(zhǔn)確度比較見表3,。

wlw1-b3.gif

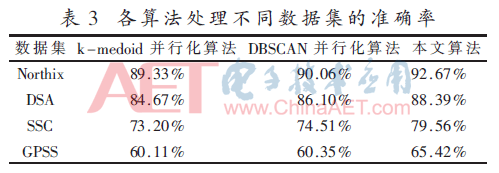
    本文算法的聚類準(zhǔn)確度均高于k-medoids并行化算法和DBSCAN并行化算法,，并且在處理較大數(shù)量級的數(shù)據(jù)集時，本文算法準(zhǔn)確度更占優(yōu)勢,。不同數(shù)據(jù)集上各算法的執(zhí)行時間如圖2,。

wlw1-t2.gif

    根據(jù)圖2，隨著數(shù)據(jù)量的增大,，三種算法執(zhí)行效率差異逐漸增大,，本文算法性能明顯優(yōu)于k-medoids并行性算法和DBSCAN并行算法。接著對三個算法使用7個線程時的執(zhí)行時間進(jìn)行比較,，如圖3所示,。

wlw1-t3.gif

    從圖3中可以看出,，使用7個線程在1 000、5 000,、10 000數(shù)據(jù)級時,，本文算法執(zhí)行時間明顯優(yōu)于其他兩個算法。

3.3 實(shí)驗(yàn)小結(jié)

    仿真實(shí)驗(yàn)可知,，在同一線程數(shù)時,，本文算法比對比算法聚類準(zhǔn)確率高，執(zhí)行時間短,；在線程數(shù)增加時，本文算法執(zhí)行時間顯著降低,；隨著數(shù)據(jù)量的增長,，本文算法在保證更高準(zhǔn)確度的基礎(chǔ)上，執(zhí)行時間優(yōu)勢逐漸凸顯,。

4 結(jié)論

    本文針對電力通信數(shù)據(jù)的聚類處理問題,，提出基于密度的聚類思想對k-medoids算法初始點(diǎn)的選取策略進(jìn)行優(yōu)化，并利用MapReduce編程框架實(shí)現(xiàn)了算法的并行化處理,。通過仿真實(shí)驗(yàn)表明本文提出的優(yōu)化算法可行有效,，并具有較好的執(zhí)行效率。在接下來的研究中可以考慮線程數(shù)小于聚類數(shù)時的優(yōu)化分配策略,，進(jìn)一步提高算法性能,。

參考文獻(xiàn)

[1] 蔡永強(qiáng)，陳平華,，李惠.基于云計(jì)算平臺的并行DBSCAN算法[J].廣東工業(yè)大學(xué)學(xué)報,2016,，33(1)：51-56.

[2] PARK H S，JUN C H.A simple and fast algorithm for k-medoids clustering[J].Expert System with Applications,，2009,，36(2)：3336-3341.

[3] 趙燁，黃澤君.蟻群K-medoids融合的聚類算法[J].電子測量與儀器學(xué)報,，2012,，26(9)：800-804.

[4] 馬菁，謝娟英.基于粒計(jì)算的k-medoids聚類算法[J].計(jì)算機(jī)應(yīng)用,，2012,，32(7)：1973-1977.

[5] 吳景嵐，朱文興.基于k中心點(diǎn)的迭代局部搜索聚類算法[J].計(jì)算機(jī)研究與發(fā)展,，2004,，41(Z)：246-252.

[6] Jiang Yaobin，Zhang Jiongmin.Parallel k-medoids clustering algorithm based on Hadoop[C].Proceedings of the IEEE International Conference on Software Engineering and Service Sciences，2014：649-651.

[7] 孫勝,，王元珍.基于核的自適應(yīng)k-medoid聚類[J].計(jì)算機(jī)工程與設(shè)計(jì),，2009，30（3）：674-677.

[8] 馬曉慧.一種改進(jìn)的可并行的K-medoids聚類算法[J].智能計(jì)算機(jī)與應(yīng)用,，2015：874-876.



作者信息:

曾  瑛,，李星南，劉新展

（廣東電網(wǎng)公司 廣東電網(wǎng)電力調(diào)度控制中心,，廣東 廣州510600）

此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。