0 引言

    恒流源是輸出穩(wěn)定電流以驅(qū)動負載工作的電源，常應(yīng)用在半導(dǎo)體光源^[1],、物性型敏感器件^[2],、充電裝置^[3]等領(lǐng)域中，而恒流源輸出電流的好壞,，直接影響光學(xué)測量精度和應(yīng)用對象使用壽命,。因此，對恒流源的研究存在積極的現(xiàn)實意義,。在對恒流源系統(tǒng)的研究中,，文獻[4]采用雙級恒流源硬件電路，用以降低電流噪聲的干擾,，并應(yīng)用于固態(tài)激光器,；文獻[5]通過諧振開關(guān)反饋控制MOS管，以解決負載的過流問題,。上述對恒流源的研究,，注重通過電路設(shè)計解決電流控制過程中產(chǎn)生的問題，但忽略了非理想狀態(tài)下系統(tǒng)噪聲和測量噪聲的存在,，以至于影響了恒流源系統(tǒng)的電流輸出效果,。

    Kalman濾波算法可以有效解決控制過程中由噪聲干擾引起的誤差^[6],，分數(shù)階PID（Fractional Order Proportional Integral Differential，F(xiàn)OPID）在溫度系統(tǒng)^[7],、生物反應(yīng)器^[8]等應(yīng)用中控制效果顯著,。為改善恒流源的輸出效果，本文提出將Kalman濾波算法與FOPID控制策略相結(jié)合,，構(gòu)建Kalman-FOPID控制器,，并對恒流源電路進行數(shù)學(xué)建模，在利用MATLAB對Kalman-FOPID控制器的控制效果驗證的基礎(chǔ)上,，進行硬件測試。實驗結(jié)果表明,，Kalman-FOPID控制器能夠有效濾除系統(tǒng)中的噪聲干擾,，提高電流的輸出精度，使系統(tǒng)穩(wěn)定可靠,。

1 恒流源系統(tǒng)與數(shù)學(xué)建模

1.1 恒流源系統(tǒng)結(jié)構(gòu)

    恒流源系統(tǒng)結(jié)構(gòu)如圖1所示,，用戶輸入設(shè)定電流值，主控芯片根據(jù)設(shè)定值輸出占空比為D的PWM波,，經(jīng)驅(qū)動電路控制BUCK電路中MOS管通斷,，以調(diào)整加在負載兩端的電壓，而流過負載的電流值經(jīng)電流采樣,、A/D轉(zhuǎn)換為數(shù)字量后送入主控芯片內(nèi),，主控芯片根據(jù)電流設(shè)定值與實際值的偏差調(diào)整PWM的占空比，以實現(xiàn)流過負載電流的穩(wěn)定,。

1.2 恒流源系統(tǒng)的數(shù)學(xué)模型

    本文恒流源電路是基于BUCK電路來實現(xiàn)的,，通過控制MOS管的通斷改變負載兩端的電壓，以使流過負載的電流保持恒定,，在忽略電感電阻和電容電阻條件下,，電路原理圖如圖2所示。

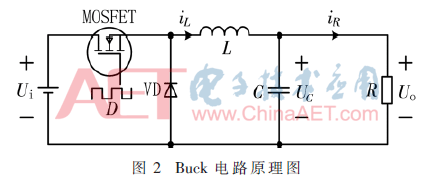
    設(shè)恒流源的輸入電壓為U_i,，驅(qū)動MOSFET的PWM波占空比為D,，周期為T，電感電流為i_L,，電容電壓為U_C,，負載R兩端電壓為U_O，流過負載電流為i_R,。通過增大電感L,，使BUCK電路工作在連續(xù)工作模式下。在任意t∈[t_i-1,，t_i]時刻,，i=1,，2，3…,，有：

    (1)在t∈[t_i-1,，DT+t_i-1]時，PWM波為高電平,，驅(qū)動MOS管導(dǎo)通,，此時電路的狀態(tài)空間方程為：

2 Kalman-FOPID控制器設(shè)計

2.1 FOPID控制算法

    FOPID的頻域形式為：

    式中K_p、K_i,、K_d為比例,、積分、微分系數(shù),，λ,、μ分別是積分、微分的階數(shù),。IOPID是FOPID在λ=1,、μ=1的特殊情況，有固定的整定方法,，實現(xiàn)簡單,，但只有3個可調(diào)參數(shù)；FOPID有5個可調(diào)參數(shù),，雖然整定方法復(fù)雜,，但參數(shù)設(shè)置靈活，控制效果較好,，且魯棒性強,。FOPID在時域的形式為：

2.2 Kalman-FOPID控制器

    Kalman-FOPID控制系統(tǒng)框圖如圖3所示。將電流設(shè)定值x與實際值y的偏差e送入FOPID控制器中,，輸出u在受系統(tǒng)噪聲q的干擾后驅(qū)動BUCK電路中MOS管通斷,，使負載工作；對負載電流采樣時,，采樣值與實際值之間存在測量噪聲r,，利用Kalman濾波算法降低噪聲q和r的影響，使電流實際值y準(zhǔn)確反饋到控制器,，以實現(xiàn)閉環(huán)控制,。

    Kalman-FOPID控制算法流程：

    (1)對恒流源系統(tǒng)的傳遞函數(shù)進行z變換，得到離散型線性系統(tǒng)時域形式：

    (4)根據(jù)設(shè)定值與觀測值的誤差e采用FOPID控制算法調(diào)整輸出z_k,；

    (5)測量更新：

    計算Kalman增益K_k：

    更新誤差協(xié)方差P_k：

    (6)重復(fù)步驟(3)到步驟(5),，進行下一次Kalman-FOPID控制，直到輸出電流滿足系統(tǒng)要求,。

3 實驗分析

    為了探究 Kalman-FOPID控制器對存在系統(tǒng)噪聲和測量噪聲干擾的恒流源系統(tǒng)的控制效果,，采用MATLAB軟件依次使用IOPID,、FOPID、Kalman-IOPID,、Kalman-FOPID 4種控制策略進行仿真,，比較4種控制策略之間的控制效果，并利用硬件驗證Kalman-FOPID應(yīng)用在恒流源系統(tǒng)的可行性和控制效果,。

3.1 仿真研究

    根據(jù)恒流源系統(tǒng)的數(shù)學(xué)模型,，設(shè)計參數(shù)為：U_i=12 V，L=2 H,，C=4 400 μF,，R=10 Ω，Ts=0.000 1 s,，仿真時間為1 s,。此時系統(tǒng)的流控型傳遞函數(shù)為：

    恒流源系統(tǒng)中存在的系統(tǒng)噪聲與測量噪聲，是利用MATLAB的隨機函數(shù)rand()產(chǎn)生的,，幅值為0.000 2。Kalman濾波算法中的參數(shù)初始化為：Q=1,、R=1,；各控制器的參數(shù)采用粒子群算法尋優(yōu)并結(jié)合試驗法得出最優(yōu)值，具體如表1所示,。

    當(dāng)控制系統(tǒng)輸入為階躍響應(yīng),，幅值為1 A時，4種控制策略響應(yīng)曲線及特性如下：

    (1)IOPID與FOPID響應(yīng)曲線

    IOPID與FOPID在響應(yīng)過程中受隨機噪聲的干擾,，每次仿真的結(jié)果各不相同,，圖4是仿真結(jié)果之一，為了比較IOPID和FOPID的控制效果,，連續(xù)仿真50次,，統(tǒng)計各自最大超調(diào)量偏差、0.1 s后響應(yīng)過程的最大波動誤差,，統(tǒng)計結(jié)果如圖5所示,。

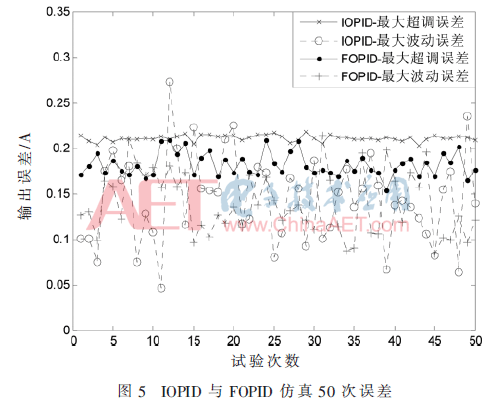
    在多次仿真過程中，IOPID響應(yīng)曲線在0.000 5 s達到最大超調(diào)量,，且超調(diào)量比較穩(wěn)定,；FOPID響應(yīng)曲線在0.001 2 s達到最大超調(diào)量，超調(diào)量波動較大,，但總體小于IOPID的最大超調(diào)量,；IOPID與FOPID在響應(yīng)時間0.1 s后的最大波動誤差變化都比較大。因此,，IOPID與FOPID在有噪聲干擾的恒流源系統(tǒng)中控制效果較差,。

    (2)Kalman-IOPID與Kalman-FOPID響應(yīng)曲線

    Kalman-IOPID與Kalman-FOPID中Kalman濾波算法可以有效降低隨機噪聲的干擾,，多次仿真的結(jié)果相同，響應(yīng)曲線如圖6所示,。

    根據(jù)圖6仿真曲線,，控制策略的上升時間t_r、穩(wěn)態(tài)時間t_s,、穩(wěn)態(tài)誤差e_ss的參數(shù)如表2所示,。與Kalman-IOPID相比，Kalman-FOPID上升時間t_r較長,，但從響應(yīng)到穩(wěn)態(tài)的時間為0.338 8 s,，小于Kalman-IOPID的0.636 0 s，并且穩(wěn)態(tài)誤差也較小,。因此,，Kalman-IOPID與Kalman-FOPID可以有效控制存在噪聲的恒流源系統(tǒng)，其中Kalman-FOPID從響應(yīng)到穩(wěn)態(tài)的時間短,，穩(wěn)態(tài)誤差小,。

    通過采用MATLAB進行仿真研究可知，Kalman濾波算法可以降低隨機噪聲對系統(tǒng)的影響,，將Kalman濾波算法與FOPID控制策略相結(jié)合的Kalman-FOPID控制器理論上可以控制存在噪聲干擾的流控型恒流源系統(tǒng),，并取得較好控制的效果。

3.2 硬件測試

    為進一步驗證Kalman-FOPID算法控制效果,，根據(jù)圖1設(shè)計恒流源電路,，采用Kalman-FOPID控制算法，硬件測試過程如下：

    (1)當(dāng)設(shè)定電流較小時,，為了降低采樣電阻的影響,，選擇較大的負載電阻。選取阻值為16.8 Ω,，依次設(shè)定電流值,，測量數(shù)據(jù)如表3所示。

    (2)當(dāng)設(shè)定電流較大時,，為使系統(tǒng)輸出較大電流,，負載電阻應(yīng)當(dāng)較小。調(diào)整負載電阻為8.2 Ω時,，不同設(shè)定電流值的測量數(shù)據(jù)如表4所示,。

    由測量數(shù)據(jù)可知，在小電流控制時,，負載電阻為16.8 Ω時最大電流誤差為0.04 mA,；在大電流輸出時，負載電阻為8.2 Ω時最大電流誤差為0.53 mA。電流的設(shè)定值與實際值誤差較小,，表明Kalman-FOPID控制策略可應(yīng)用于恒流源系統(tǒng)中,，并且有效降低系統(tǒng)中噪聲干擾，輸出電流穩(wěn)定,、控制精度高,。

4 結(jié)論

    本文針對恒流源系統(tǒng)中存在的系統(tǒng)噪聲和測量噪聲的干擾問題，提出了將Kalman濾波算法和FOPID控制策略相結(jié)合,，構(gòu)建Kalman-FOPID控制器,，在建立以BUCK電路為核心的流控型恒流源系統(tǒng)數(shù)學(xué)模型的基礎(chǔ)上，合理設(shè)置參數(shù),，利用MATLAB模擬噪聲干擾,，進行恒流源的控制仿真。仿真結(jié)果表明Kalman-IOPID和Kalman-FOPID可以降低系統(tǒng)中噪聲的干擾,，輸出電流的控制性能參數(shù)較好,，其中Kalman-FOPID到達穩(wěn)態(tài)的時間較短、穩(wěn)態(tài)誤差較小,。通過搭建恒流源硬件控制系統(tǒng)實驗電路,，通過調(diào)整負載情況，觀察測量電流輸出,，實驗結(jié)果表明電流穩(wěn)定性好,、控制精度高，能夠應(yīng)用于對電流輸出要求高的工業(yè)場所,，尤其是對電流變化敏感的半導(dǎo)體光源,，對其亮度質(zhì)量的控制和使用壽命的延長起到促進作用,。

參考文獻

[1] CHEN K,，XIAO P，JOHNSEN A,，et al.Turn-on optimization for class D series-parallel LCC-type constant current high-power LED driver design based on traditional fluorescent control IC[J].IEEE Transactions on Power Electronics,，2016，31(7)：4732-4741.

[2] 許偉明,，李瑜煜,，葉健聰.熱電材料電阻率測量的專用恒流源[J].實驗室研究與探索，2016,，35(7)：143-148.

[3] TRAN D H,，VU V B,，CHOI W.Design of a high efficiency wireless power transfer system with intermidiate coils for the on-board chargers of electric vehicles[J].IEEE Transactions on Power Electronics,，2018,，33(1)：175-187.

[4] DUDZIK G.Ultra-stable, low-noise two-stage current source concept for electronics and laser applications[J].IET Circuits Devices & Systems，2017，11(6)：613-617.

[5] LIN H,，HSIAO K C.Development of load constant current model using feedback-controlling resonant switching algorithm for overload protection[J].IET Circuits Devices & Systems,，2017，11(6)：656-665.

[6] 楊輝,，郝麗娜,，陳洋，等.針對氣動肌肉仿生肘關(guān)節(jié)抖振現(xiàn)象的Kalman-PID控制[J].控制理論與應(yīng)用,，2017,，34(4)：477-482.

[7] 秦君琴，李興財,，楊有貞.分數(shù)階PID控制器在蔬菜大棚溫度控制中的應(yīng)用研究[J].西南大學(xué)學(xué)報(自然科學(xué)版),，2016，38(1)：179-182.

[8] ESTAKHROUIYEH M R,，VALI M,，GHARAVEISI A.Application of fractional order iterative learning controller for a type of batch bioreactor[J].IET Control Theory & Applications，2016,，10(12)：1374-1383.

[9] PETRAS I.Fractional-order nonlinear controllers: Design and implementation notes[C].Carpathian Control Conference.IEEE,，2016：579-583.

作者信息：

曹珍貫，余俊峰,，李智威

（安徽理工大學(xué) 電氣與信息工程學(xué)院,，安徽 淮南232001）