0 引言

    無(wú)線射頻識(shí)別(Radio Frequency Identification，RFID)是一種利用射頻識(shí)別方式進(jìn)行無(wú)線非接觸雙向通信的自動(dòng)識(shí)別技術(shù),。隨著物聯(lián)網(wǎng)技術(shù)的日益成熟,，RFID技術(shù)得到了快速的發(fā)展，但其存在的問(wèn)題也越來(lái)越凸顯出來(lái),。目前RFID技術(shù)的主要問(wèn)題包括：標(biāo)準(zhǔn)不統(tǒng)一問(wèn)題,、數(shù)據(jù)安全問(wèn)題、電磁干擾問(wèn)題,、標(biāo)簽碰撞問(wèn)題等,，其中標(biāo)簽碰撞問(wèn)題嚴(yán)重制約著RFID的發(fā)展，如何有效解決標(biāo)簽碰撞問(wèn)題是RFID技術(shù)研究的重點(diǎn)和難點(diǎn),。目前解決標(biāo)簽碰撞問(wèn)題的防碰撞算法主要分為兩類^[1]：基于樹類的確定性算法和基于ALOHA類的隨機(jī)性防碰撞算法,。

    基于樹類的確定性算法分為二進(jìn)制樹(Binary Search Tree，BT)類和查詢樹(Query Tree,，QT)類算法,。在BT類算法中，讀寫器逐時(shí)隙生成隨機(jī)數(shù)0和1,，進(jìn)而形成新的路徑來(lái)識(shí)別標(biāo)簽,。在QT類算法中，讀寫器根據(jù)標(biāo)簽ID的二進(jìn)制樹狀結(jié)構(gòu)特點(diǎn),，形成唯一響應(yīng)路徑的策略來(lái)識(shí)別標(biāo)簽,。學(xué)者們根據(jù)樹類算法的特點(diǎn)，提出大量改進(jìn)的防碰撞算法^[2-6],，但仍產(chǎn)生大量的空閑和碰撞時(shí)隙,。基于ALOHA的隨機(jī)性算法^[7-11]采用時(shí)隙隨機(jī)分配的工作方式,，執(zhí)行過(guò)程相對(duì)簡(jiǎn)單,，易于實(shí)現(xiàn)。當(dāng)前該類算法又主要分為動(dòng)態(tài)幀時(shí)隙算法(Dynamic Frame Slot Aloha,，DFSA）和Q算法,。前者通過(guò)將幀長(zhǎng)設(shè)定為估計(jì)標(biāo)簽數(shù)量的近似值，使系統(tǒng)以最高的效率識(shí)別標(biāo)簽,，標(biāo)簽數(shù)量估算精度和幀長(zhǎng)的動(dòng)態(tài)調(diào)整是制約DFSA算法識(shí)別效率的主要原因,。后者避免了待識(shí)別標(biāo)簽數(shù)量的估計(jì),，同時(shí)解決了DFSA算法在識(shí)別幀中不能動(dòng)態(tài)調(diào)整幀長(zhǎng)的問(wèn)題，但其使用單一的調(diào)整因子不能單獨(dú)考慮空閑時(shí)隙和碰撞時(shí)隙,。

    本文針對(duì)DFSA類算法對(duì)幀長(zhǎng)調(diào)整的不靈敏性以及Q算法中Q值調(diào)整的高計(jì)算復(fù)雜度，提出了基于連續(xù)時(shí)隙探測(cè)的RFID防碰撞算法(Continuous Slot Detection,，CSD),。CSD算法引入了時(shí)隙探測(cè)的概念，通過(guò)判斷識(shí)別幀中連續(xù)時(shí)隙的應(yīng)答情況,，動(dòng)態(tài)調(diào)整幀長(zhǎng),。仿真結(jié)果顯示，與其他防碰撞算法相比,，CSD算法具有較低的識(shí)別時(shí)延和較快的識(shí)別速度,，并且在較多標(biāo)簽存在的環(huán)境下有明顯優(yōu)勢(shì)。

1 連續(xù)時(shí)隙探測(cè)的防碰撞算法

1.1 CSD算法思想

    針對(duì)DFSA類算法對(duì)幀長(zhǎng)調(diào)整的不靈敏性以及Q算法中Q值調(diào)整的高計(jì)算復(fù)雜度,，本文提出的CSD算法主要有以下兩個(gè)方面的改進(jìn)：

    (1)緩解標(biāo)簽識(shí)別初始階段的標(biāo)簽與幀長(zhǎng)不匹配問(wèn)題,。對(duì)于DFSA算法，無(wú)論當(dāng)前時(shí)隙是空閑還是碰撞,，讀寫器都要查閱完整個(gè)時(shí)隙才能調(diào)整幀長(zhǎng),，因此在標(biāo)簽與幀長(zhǎng)不匹配的初始階段，DFSA無(wú)法迅速根據(jù)標(biāo)簽數(shù)量調(diào)整幀長(zhǎng),。CSD算法結(jié)合理論分析和實(shí)驗(yàn)推導(dǎo),，在大規(guī)模標(biāo)簽群下，通過(guò)判斷初始條件下待識(shí)別幀起始3個(gè)連續(xù)時(shí)隙的應(yīng)答狀況,，迅速調(diào)整幀長(zhǎng),，使系統(tǒng)工作在最優(yōu)狀態(tài)。

    (2)降低浮點(diǎn)數(shù)運(yùn)算的計(jì)算復(fù)雜度,。計(jì)算機(jī)中所有的數(shù)據(jù)均以二進(jìn)制形式表示,，浮點(diǎn)數(shù)也不例外。當(dāng)在大規(guī)模標(biāo)簽群時(shí),，讀寫器多次對(duì)浮點(diǎn)參數(shù)進(jìn)行近似計(jì)算,，不僅造成誤差累加，而且降低系統(tǒng)的識(shí)別效率,。CSD算法利用判斷幀中連續(xù)3個(gè)時(shí)隙的狀態(tài)替代浮點(diǎn)參數(shù)c調(diào)整幀長(zhǎng),，降低了運(yùn)算量，加快了識(shí)別速度,。

1.2 CSD算法關(guān)鍵參數(shù)的確定

    為了詳細(xì)描述CSD算法,，現(xiàn)定義以下概念：

    定義1 標(biāo)簽幀長(zhǎng)比α為待識(shí)別標(biāo)簽數(shù)量n與識(shí)別幀長(zhǎng)F的比值：

    定義2 單位碰撞標(biāo)簽量β_k為連續(xù)碰撞時(shí)隙內(nèi)的每個(gè)時(shí)隙的標(biāo)簽量，k為連續(xù)狀態(tài)相同的時(shí)隙個(gè)數(shù),。

    定義3 η_k表示連續(xù)k個(gè)空閑時(shí)隙發(fā)生的概率,。

    定義4 γ_k表示連續(xù)k個(gè)碰撞時(shí)隙發(fā)生的概率,。

    定義5 連續(xù)碰撞時(shí)隙計(jì)數(shù)器(Continuous Collision Slot Count，CCSC)用于統(tǒng)計(jì)連續(xù)碰撞時(shí)隙的數(shù)量,；連續(xù)空閑時(shí)隙計(jì)數(shù)器(Continuous Idle Slot Count,，CISC)用于統(tǒng)計(jì)連續(xù)空閑時(shí)隙的數(shù)量。

1.2.1 連續(xù)空閑時(shí)隙數(shù)量的確定

    標(biāo)簽的碰撞問(wèn)題從數(shù)學(xué)的角度上說(shuō)是一個(gè)多重伯努利實(shí)驗(yàn)問(wèn)題,。理論條件下一個(gè)時(shí)隙內(nèi)出現(xiàn)r個(gè)標(biāo)簽可以記為：

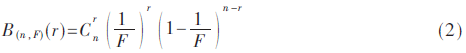
    因此,，對(duì)于幀長(zhǎng)中k個(gè)連續(xù)時(shí)隙全部為空閑的概率為：

    采用Python 2.7對(duì)式(5)進(jìn)行描點(diǎn)，得到了在不同k值下標(biāo)簽幀長(zhǎng)比α與連續(xù)個(gè)空閑時(shí)隙發(fā)生的概率η_k之間的關(guān)系,，如圖1所示,。

    從圖1中可以看出，α與η_k成反比關(guān)系,，α值越大,，η_k值越小，這是因?yàn)楫?dāng)標(biāo)簽的數(shù)量大于幀長(zhǎng)時(shí),，每一個(gè)時(shí)隙內(nèi)平均存在的標(biāo)簽數(shù)量不少于1個(gè),，因此出現(xiàn)連續(xù)空閑時(shí)隙的概率是不斷減小的；同時(shí),，在相同α值下,，k與η_k也成反比關(guān)系。

    當(dāng)α>0.75,，k≥3時(shí),，有：

    即當(dāng)α≤0.75時(shí)，結(jié)合式(6),、式(8)和式(9),，k=η_min(i)，i≥3,，即k=3,。因此，可認(rèn)定當(dāng)幀中出現(xiàn)連續(xù)3個(gè)空閑時(shí)隙時(shí),，此時(shí)的幀長(zhǎng)與待識(shí)別標(biāo)簽數(shù)量不匹配,，需要重新調(diào)整幀長(zhǎng)識(shí)別。

    文獻(xiàn)[9]中已證明,，當(dāng)待識(shí)別的幀長(zhǎng)F與標(biāo)簽數(shù)量n近似相等時(shí),，系統(tǒng)會(huì)得到最大的識(shí)別效率。結(jié)合式(8)和式(9),，以F/2的標(biāo)簽估計(jì)誤差小于F時(shí)的誤差,，即標(biāo)簽的數(shù)量近似于F/2，則調(diào)整當(dāng)前幀長(zhǎng)為F/2，得到最佳的系統(tǒng)效率,。

1.2.2 連續(xù)碰撞時(shí)隙數(shù)量的確定

    根據(jù)式(2),，對(duì)于幀長(zhǎng)中出現(xiàn)連續(xù)k個(gè)碰撞時(shí)隙的概率γ_k可計(jì)算為：

    為了便于描述β的取值范圍，同時(shí)考慮到β₁,，β₂,，…，β_k的值遠(yuǎn)小于待識(shí)別標(biāo)簽的數(shù)量,，現(xiàn)令β₁,，β₂，…,，β_k∈[2,，t],，t<<n,，對(duì)式(12)進(jìn)行描點(diǎn)，得到了在不同k值下α與γ_k成反比關(guān)系,，如圖2所示,。

    從圖2(a)中可以看出，當(dāng)k=2,，α→2時(shí),，無(wú)論t取何值，γ₂的值都近似為1,，即標(biāo)簽的數(shù)量為幀長(zhǎng)兩倍的條件下,，識(shí)別幀中一定出現(xiàn)兩個(gè)連續(xù)碰撞時(shí)隙；從圖2(c)中可以看出,，當(dāng)k=4時(shí),，在無(wú)論t取何值，γ的值都很小趨近于0,，這是因?yàn)楫?dāng)有α值較小時(shí),，發(fā)生連續(xù)碰撞的概率本來(lái)就是小概率事件，而當(dāng)α值較大時(shí),，其值又受限于β的取值,。

    對(duì)于k=3，當(dāng)α>1.5,，t≥10時(shí),，有：

    當(dāng)幀中出現(xiàn)連續(xù)3個(gè)碰撞時(shí)隙時(shí)，以2·F的標(biāo)簽估計(jì)誤差小于F時(shí)的誤差,，即標(biāo)簽的數(shù)量接近2·F,，則調(diào)整當(dāng)前幀長(zhǎng)為2·F，得到最佳的系統(tǒng)效率。

2 仿真實(shí)驗(yàn)與分析

    本節(jié)利用計(jì)算機(jī)仿真的實(shí)驗(yàn)結(jié)果驗(yàn)證本文提出的算法,。標(biāo)簽數(shù)目分別為100,，200，…,，1000,。每設(shè)置1次標(biāo)簽數(shù)目，實(shí)驗(yàn)重復(fù)100次取平均值,。本文主要從識(shí)別時(shí)延,、最優(yōu)幀平均查詢次數(shù)和識(shí)別速度3個(gè)方面分析CSD算法。

2.1 識(shí)別時(shí)延

    在常規(guī)標(biāo)簽群下(標(biāo)簽數(shù)量從100～1 000遞增變化),，將CSD算法與傳統(tǒng)的DFSA算法和Q算法的識(shí)別時(shí)延進(jìn)行比較,，對(duì)比結(jié)果如圖3所示。因?yàn)镃SD算法通過(guò)對(duì)連續(xù)時(shí)隙的探測(cè),，利用幀長(zhǎng)調(diào)整規(guī)則,，迅速調(diào)整到最優(yōu)幀長(zhǎng)。在標(biāo)簽數(shù)量為1 000時(shí),，CSD算法的總時(shí)隙數(shù)為2 911個(gè),，比LB、Schoute,、Vgot和QA分別降低了12%,、10%、9%和4%,。

2.2 最優(yōu)幀平均查詢次數(shù)

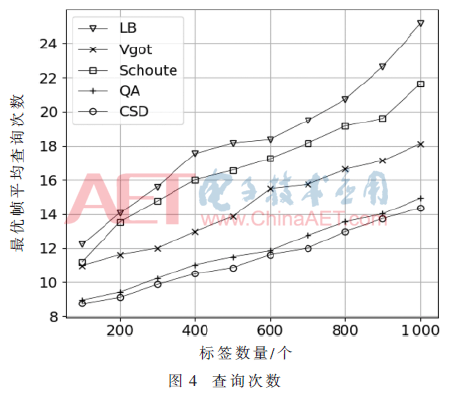
    在常規(guī)標(biāo)簽群下(標(biāo)簽數(shù)量從100～1 000遞增變化),，將CSD算法與傳統(tǒng)的DFSA算法和Q算法的最優(yōu)幀平均查詢次數(shù)進(jìn)行對(duì)比，最優(yōu)幀平均查詢次數(shù)定義為系統(tǒng)從初始幀長(zhǎng)調(diào)整到最優(yōu)幀長(zhǎng)下讀寫器重發(fā)布幀長(zhǎng)調(diào)整命令的次數(shù),，對(duì)比結(jié)果如圖4所示,。可以看出,，CSD算法要優(yōu)于其他算法,。在標(biāo)簽量為1 000時(shí)，CSD算法比QA算法和Vgot算法分別減少了6%和22%的查詢次數(shù),。

2.3 識(shí)別速度

    在常規(guī)標(biāo)簽群下(標(biāo)簽數(shù)量從100～1 000遞增變化),，將CSD算法與傳統(tǒng)的DFSA算法和Q算法的識(shí)別速度進(jìn)行對(duì)比，對(duì)比結(jié)果如圖5所示,。LB算法和Schoute算法的讀取速度分別約為250和260,，QA算法的讀取速度約為290，而CSD算法的讀取速度最快,，約為310,，比LB算法、Schoute算法、QA算法分別提高了24%,、19%,、6%。

3 結(jié)論

    本文提出了基于連續(xù)時(shí)隙探測(cè)的RFID防碰撞算法CSD,。該算法利用數(shù)學(xué)模型及描點(diǎn)方式得出通過(guò)判斷3個(gè)連續(xù)時(shí)隙的狀況,，動(dòng)態(tài)調(diào)整幀長(zhǎng)，解決了DFSA類算法對(duì)幀長(zhǎng)調(diào)整的不靈敏性以及Q算法中Q值調(diào)整高計(jì)算復(fù)雜度的缺點(diǎn),。仿真結(jié)果顯示,，在標(biāo)簽數(shù)量為1 000的條件下，CSD算法比QA算法減少了4%的識(shí)別時(shí)延,、降低了6%的查詢次數(shù)以及提升了6%的標(biāo)簽識(shí)別速度,。

    本文通過(guò)數(shù)學(xué)模型推導(dǎo)出了識(shí)別幀中出現(xiàn)不同數(shù)量連續(xù)時(shí)隙的概率，對(duì)于求值都采用數(shù)據(jù)描點(diǎn)的方式,，因此下一步的工作是優(yōu)化數(shù)學(xué)模型的求值方法,，進(jìn)而能夠通過(guò)理論方式求出其解。

參考文獻(xiàn)

[1] FINKENZELLER K.RFID Handbook：Radio-frequency identification fundamentals and applications(Second Edition)[M].England：John Wiley and Sons,，2003.

[2] JIA X,，F(xiàn)ENG Q,，YU L.Stability analysis of an efficient anti-collision protocol for RFID tag identification[J].IEEE Transactions on Communications,，2012，60(8)：2285-2294.

[3] SHIN J,，JEON B,，YANG D.Multiple RFID tags identification with M-ary query tree scheme[J].IEEE Communications Letters，2013,，17(3)：604-607.

[4] 吳躍前,，辜大光，范振粵,，等.RFID系統(tǒng)防碰撞算法比較分析及其改進(jìn)算法[J].計(jì)算機(jī)工程與應(yīng)用,，2009(3)：210-213.

[5] 黃瓊，凌江濤,，張敏,，等.LRST：低冗余搜索樹防碰撞算法[J].通信學(xué)報(bào)，2014,，35(6)：110-116.

[6] LAI Y C,，HSIAO L Y，CHEN H J,，et al.A novel query tree protocol with bit tracking in RFID tag identification[J].IEEE Transactions on Mobile Computing,，2013，12(10)：2063-2075.

[7] 任守綱，楊帆,，徐煥良.一種雙權(quán)重參數(shù)的RFID防碰撞Q值算法研究[J].計(jì)算機(jī)科學(xué),，2014，41(4)：256-259.

[8] 吳海鋒,，曾玉.RFID動(dòng)態(tài)幀時(shí)隙ALOHA防沖突中的標(biāo)簽估計(jì)和幀長(zhǎng)確定[J].自動(dòng)化學(xué)報(bào),，2010，36(4)：620-624.

[9] 任守綱,，楊帆,，王浩云，等.基于判決門限的RFID防碰撞Q值算法[J].計(jì)算機(jī)科學(xué),，2014,，41(8)：154-157.

[10] 張小紅，張留洋.RFID防碰撞時(shí)隙應(yīng)變協(xié)處理算法研究[J].電子學(xué)報(bào),，2014,，42(6)：1139-1146.

[11] 楊帆，徐煥良,，謝俊,，等.基于雙空閑因子的RFID防碰撞算法研究[J].計(jì)算機(jī)工程與科學(xué)，2016,，38(7)：1440-1446.

作者信息:

楊  帆1,，任守綱2，郝水俠1,，周  俊3,，袁培森2

(1.江蘇師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，江蘇 徐州221116,；

2.南京農(nóng)業(yè)大學(xué) 信息科學(xué)技術(shù)學(xué)院,，江蘇 南京210095；

3.南京農(nóng)業(yè)大學(xué) 江蘇省智能農(nóng)業(yè)裝備重點(diǎn)實(shí)驗(yàn)室,，江蘇 南京210031)