0 引言

    DC-DC開關變換器在電力電子工業(yè),、軍工系統(tǒng)中有著十分廣泛的應用^[1],。并且手持式電子設備、移動手機等用電設備對供電電源的輕載效率,、瞬態(tài)響應特性以及負載范圍提出了更高的要求^[2],。因此，對開關DC-DC變換器控制決策的改進成為了越來越多的科研工作者研究的重點,，并促使大量科研工作者對數字DC-DC控制進行研究,，取得了相當大的成果。

    文獻[3]為了提高DC-DC變換器的瞬態(tài)響應性能,，設計了一款基于數字預測的模糊PID控制器,，通過預測機制實現了瞬態(tài)響應的提高，并通過數字FPGA控制器進行驗證,；文獻[4]基于數字PID控制設計了一款高精度的可調LED恒流驅動器,，詳細介紹了恒流源的設計過程，但沒有對于數字PID參數的設計進行詳細分析,；文獻[5]基于數字PID提出了混合控制模式的策略,，通過對輸入電壓和電流波形進行控制，較好地實現了功率因數校正,，DC-DC Boost變換器轉換效率達到91%,；文獻[6]基于可編程門陣列（FPGA）實現了DC-DC Buck變換器的數字控制，通過對廣義比例積分（GPI）控制器和比例積分微分（PID）控制器進行比較,，得出了GPI控制在擾動抑制方面有更好的動態(tài)響應,；文獻[7]提出了一種基于微處理器的電流跟蹤數字控制，實現了在輸入電壓突變,、負載突變以及啟動過程中具有較好的動態(tài)性能,；文獻[8]、[9]提出非線性PID數字控制,，通過仿真驗證了在不同負載變化下的啟動瞬態(tài)響應,，非線性變換器有著更好的補償性能。

    本文在以上研究的基礎上,，擴寬數字PID控制的應用范圍,，基于對輸出電壓的采樣分析,，提出多組PID切換數字控制補償的方法。通過切換PID數字控制使得控制器可以快速響應負載或輸入電壓的變化,，同時能夠保證有良好的穩(wěn)態(tài)性能,。本文以Buck變換器為例，分析了多組PID切換數字控制器的性能,，研究和分析了其瞬態(tài)響應特性,。最終通過理論分析和仿真對比驗證了多組PID切換數字控制器具有優(yōu)越的穩(wěn)態(tài)性能和瞬態(tài)響應。

1 DC-DC Buck模型分析

    在DC-DC轉換器中,，輸出電壓是輸入線電壓,、占空比和負載電流的函數，期望在諸如輸入電壓或負載電流的突然變化之類的擾動情況下具有恒定的輸出電壓^[10],。圖1給出了Buck變換器的電路圖,。

    在式(1)中給出了Buck變換器的輸出控制小信號傳遞函數，并利用標準的狀態(tài)空間平均法得到了該函數^[9],。

    由式(2)通過MATLAB繪制開環(huán)Buck的伯德圖如圖2所示,，由圖2可知，系統(tǒng)穿越頻率為1.941 7 kHz,，同時開環(huán)Buck的相位裕度為21.9°,，增益裕度無窮大。并且由于Buck變換器輸出電壓采樣和占空比更新之間存在一個固定的周期延遲,，由函數建模，其中T為數字控制器對電壓的采樣周期(20 ?滋s),。圖3所示為帶有延遲時間的Buck變換器傳遞函數的伯德圖,。通過圖3可以得出系統(tǒng)的穿越頻率沒有發(fā)生變化，但相位裕度變?yōu)?.92°,，增益裕度為20.1 dB,。

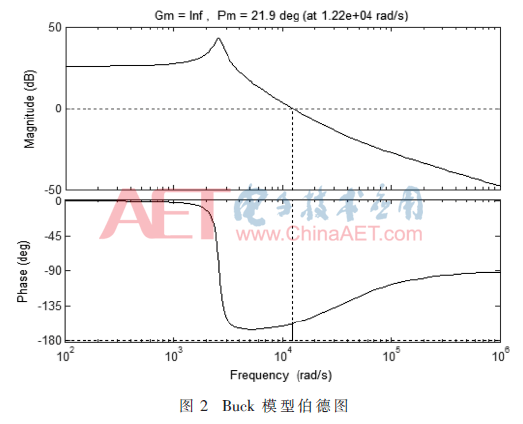
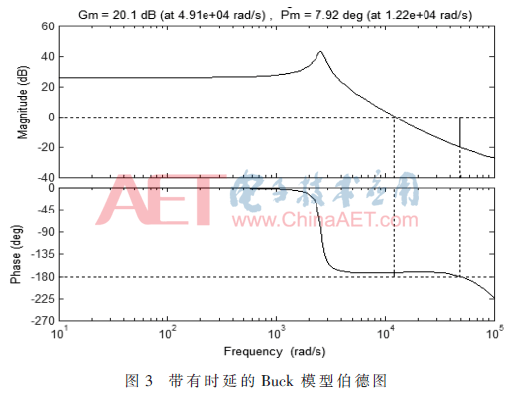
    圖3伯德圖顯示系統(tǒng)具有較小的相位裕度。因此必須要設計相應的補償器,，以確保低頻率的增益足夠高,，使得穩(wěn)態(tài)誤差最小。由文獻[11]可知在工程領域,，相位裕度Ψ_m(ω_c)=45°表示系統(tǒng)具有足夠的相位裕度,。因此補償系統(tǒng)后的相位裕度應大于45°才足以滿足瞬態(tài)響應的要求。同時,，由文獻[12]可知在工程領域中,，通常認為增益裕度K_g≥10 dB時，系統(tǒng)具有足夠的增益裕度,。本文在接下來的章節(jié)里對數字PID補償器進行了設計,。

2 數字PID設計

    如圖4所示反饋電壓信號通過與數字電壓基準作差,，得出差值作為驅動變換器占空比的控制信號，然后通過比例積分微分（PID）控制器計算更新占空比,。式(3)給出了PID控制規(guī)律的基本輸入/輸出關系的微分方程,，并由式(4)給出模擬PID控制器的傳遞函數^[10，13],。

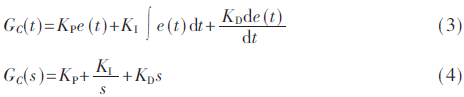
    以上公式中,，K_P是比例增益，K_I是積分增益,，K_D是微分增益,。

    PID控制器的設計在連續(xù)時間域，通過使用向后積分法（Euler法則）^[14],，可以得到式（5）所示離散時間傳遞函數變換后的差分方程^[5],。

    在式(5)中，u(k)為第k次采樣計算更新所得占空比,， e(k)為第k次的誤差,。 e(k)由式(6)計算所得，即基準電壓值與第k次輸出電壓值的誤差,。式中 e(k)- e(k-1)表示的是第k次的誤差和第k-1次的誤差差值,。    

    如圖5所示，為了使Buck電路系統(tǒng)保持良好的暫態(tài)響應和穩(wěn)態(tài)響應,，通過設計兩組PID控制器增益切換的方式補償系統(tǒng),。其中一種用于暫態(tài)期間使用為PIDI，另一種用在穩(wěn)態(tài)期間使用為PIDII,。暫態(tài)期間使用的PIDI控制器增益使其具有較高的相位裕度(≥45°)和較高的帶寬,，此PIDI設計系統(tǒng)將會產生較快的瞬態(tài)響應和較好的穩(wěn)態(tài)響應。穩(wěn)態(tài)期間使用的PIDII控制器增益使其相位裕度高于暫態(tài)相位裕度,，帶寬低于暫態(tài)期間的帶寬,，此PIDII設計系統(tǒng)將會產生較慢的瞬態(tài)響應，但是會使穩(wěn)態(tài)響應更好,。兩組PID的切換取決于第k次采樣的誤差值e(k)的大小,， 設定一個Δ值，若|e(k)|＞Δ則切換到PIDI,，若|e(k)|≤Δ則切換到PIDII,。通過PID之間的切換確定新的PWM，從而使得系統(tǒng)能夠快速地響應負載和輸入電壓的變化,，同時保持良好的穩(wěn)態(tài)性能,。

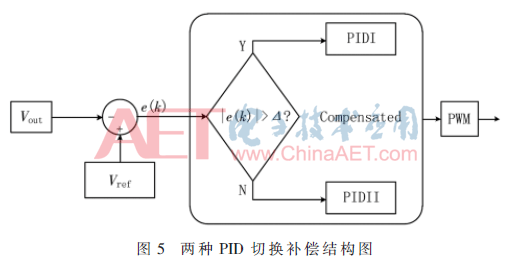
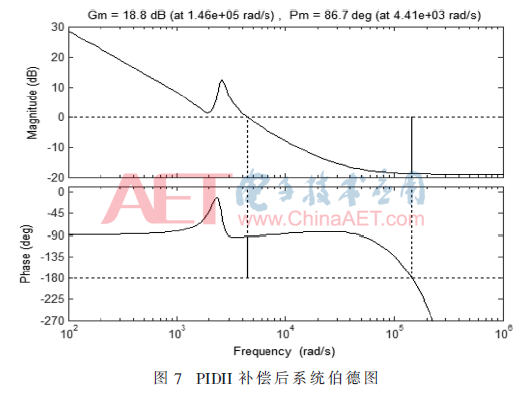
    由式（7）給出PIDI的傳遞函數，并對加入PIDI補償環(huán)節(jié)的系統(tǒng)進行伯德圖繪制,。由圖6所示,，可以得出系統(tǒng)的增益裕度K_g1=12.3 dB≥10 dB,，有足夠的增益裕度；系統(tǒng)的相位裕度Ψ_m1(ω_c)=84.4°≥45°,，有足夠的相位裕度,；系統(tǒng)穿越頻率ω_c1=1.41×10³ Hz。由式(8)給出PIDII的傳遞函數,，并對其系統(tǒng)進行伯德圖繪制,。由圖7所示，可以得出系統(tǒng)的增益裕度K_g2=18.8 dB≥10 dB,，有足夠的增益裕度,；系統(tǒng)的相位裕度Ψ_m2(ω_c)=86.7°≥45°，有足夠的相位裕度,；系統(tǒng)穿越頻率ω_c2=7.018×102 Hz,。由于穿越頻率ω_c表征系統(tǒng)的響應速度，ωc越大,，系統(tǒng)的響應速度越快,，因此PIDI的系統(tǒng)響應速度比PIDII的響應速度更快。同時由于相位裕度越大,，系統(tǒng)超調量越小,，因此PIDI的系統(tǒng)超調大于PIDII的系統(tǒng)超調。

3 仿真

    仿真的具體實現方式為：利用MATLAB/Simulink中的電氣模塊搭建仿真模型,。搭建電氣電路的時候,，利用模塊化方法，將Buck電路封裝為“DC-DC Buck Converter”子模塊,，PID補償環(huán)節(jié)封裝為“Compensated”子模塊,，使搭建的模型條理清晰，如圖8所示,。

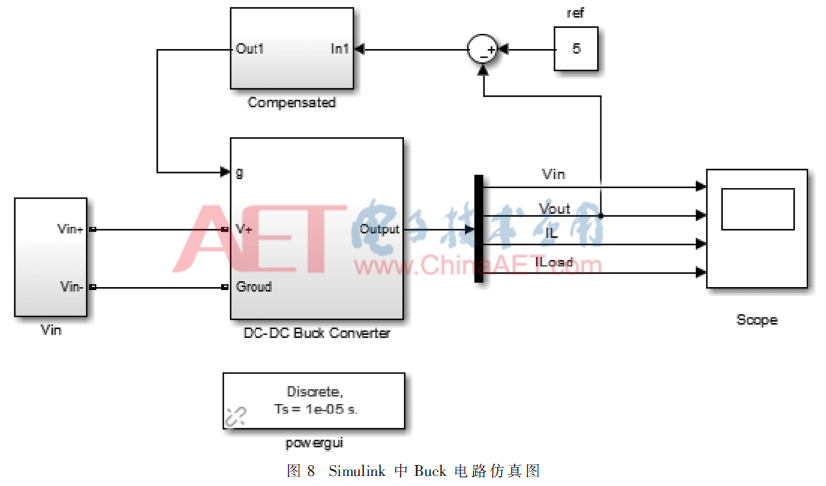
    圖8中“Compensated”子系統(tǒng)的Simulink PID切換補償仿真見圖9，“In1”輸入的為輸出電壓與參考電壓的誤差e(k),，經飽和模塊“Saturation”,，延時模塊“Transport Delay”，再經模塊“Abs”對誤差e(k)取絕對值,，在“Switch”模塊中設置“Threshold”值為0.2（即Δ=0.2 V）,，當|e(k)|＞0.2 V時PIDI模塊與PWM模塊連接產生方波，當|e(k)|≤0.2 V時PIDII模塊與PWM模塊連接產生方波,。 

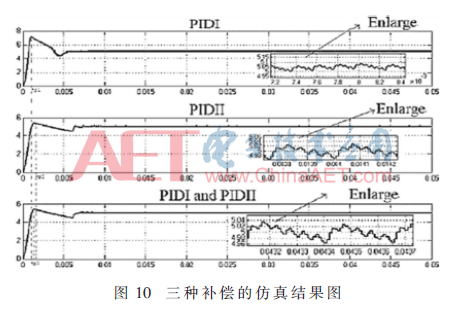
    如圖10所示,，通過仿真結果圖中的峰值時間t_p1＜t_p3＜t_p2可以得出：當只有PIDI作為補償控制時，輸出響應最快,，但同時峰值為7.5 V,，超調量σ₁=50%較大,，進入穩(wěn)態(tài)時紋波最大為0.1 V，穩(wěn)態(tài)誤差較大,；當只有PIDII作為補償控制時,，輸出信號較PIDI慢，同時峰值為5.4 V,，超調量σ₂=8%＜σ₁,，進入穩(wěn)態(tài)時紋波最大為0.03 V，穩(wěn)態(tài)誤差較??；當PIDI和PIDII切換模式作為補償控制時，輸出信號響應比PIDI慢但快于PIDII,，同時峰值約為5.45 V,，超調量σ₂＜σ₃=9%＜σ₁。通過對圖10中“PIDI and PIDII”穩(wěn)態(tài)部分進行放大,，可以得出當系統(tǒng)進入穩(wěn)態(tài)時的波紋最大為0.04 V,，系統(tǒng)電壓輸出精度高達99%以上。 

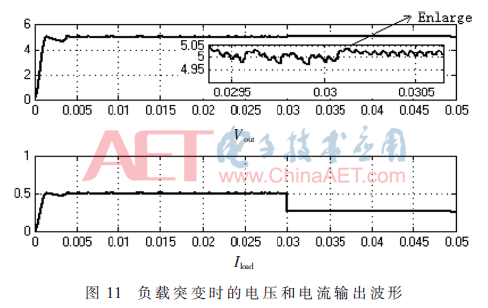
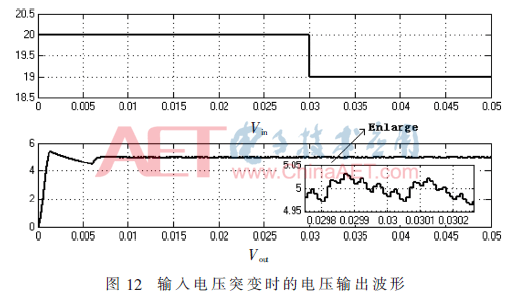
    如圖11所示,，當不改變電路其他參數的情況下,，負載電阻發(fā)生突變時，可以得出切換數字PID控制時的電路負載調整率為2%,。如圖12所示,，當不改變電路其他參數的情況下，輸入電壓突變時,，將穩(wěn)態(tài)時的輸出電壓波形圖進行放大,，可以求得輸入電壓突變情況下的系統(tǒng)電壓輸出精度高達98%以上。進一步仿真還可驗證得出,，當輸入電壓在6 V~30 V范圍內,，要求輸出參考電壓5 V的情況下，電壓實際輸出誤差率小于等于2%,。  

4 結論

    本文提出切換PID控制器改善Buck變換器穩(wěn)態(tài)性能的方法,。數字PID控制可以根據輸出電壓誤差的絕對值進行切換，這既可以實現快速的瞬態(tài)響應,，也可以產生更好的穩(wěn)態(tài)性能,。本文在Simulink中搭建仿真模型，通過Buck變換器進行測試,，仿真結果表明：(1)在保持良好的瞬態(tài)響應的同時,，可以獲得良好的穩(wěn)態(tài)性能；(2)當負載發(fā)生變化時，可以獲得較好的負載調整率,；(3)當輸入電壓發(fā)生變化時,，輸出電壓誤差率小于等于2%。

參考文獻

[1] 羅曉曙,，汪秉宏,，陳關榮，等.DC-DC buck變換器的分岔行為及混沌控制研究[J].物理學報,，2003(1)：12-17.

[2] 許麗君,，沙金，許多,，等.開關DC-DC變換器電容電流脈沖序列控制[J].電工技術學報,，2016，31(18)：100-107.

[3] 孫大鷹,，徐申,，孫偉鋒，等.Buck型DC-DC變換器中數字預測模糊PID控制器的設計與實現[J].東南大學學報(自然科學版),，2014,，44(5)：897-901.

[4] 付賢松，李圓圓,，孔旭東,，等.高精度可調光DC-DC恒流源的設計[J].電工技術學報，2015,，30(S1)：69-74.

[5] LIOU W R,，LACORTE W B，CABEROS A B,，et al.A programmable controller IC for DC/DC converter and power factor correction applications[J].IEEE Transactions on  Industrial Informatics,，2013，9(4)：2105-2113.

[6] ZURITA-BUSTAMANTE E W,，LINARES-FLORES J,，GUZMAN-RAMIREZ E，et al.A comparison between the GPI and PID controllers for the stabilization of a DC-DC “Buck” converter: A field programmable gate array implementation[J].IEEE Transactions on Industrial Electronics,，2011,，58(11)：5251-5262.

[7] 劉健，程紅麗,，王立,，等.電流跟蹤數字控制的Buck DC-DC變換器[J].電工技術學報,，2011,，26(8)：50-56，63.

[8] YOUSEFZADEH V，CHOUDHURY S.Nonlinear digital PID controller for DC-DC converters[C].2008 Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition,，IEEE,，2008：1704-1709.

[9] HE M，XU J.Nonlinear PID in digital controlled buck converters[C].Applied Power Electronics Conference,，Apec 2007-Twenty Second IEEE.IEEE,，2007：1461-1465.

[10] GUO L.Implementation of digital PID controllers for DC-DC converters using digital signal processors[C].IEEE International Conference on Electro/information Technology.IEEE，2007：306-311.

[11] MOHAN N,，UNDELAND T M,，ROBBINS W P.Power electronics：converters,applications,and design[M].John Wiley & Sons，1989.

[12] 解光軍,，程心.DC-DC開關變換器的建模與設計[M].北京：科學出版社,，2015.

[13] ASTROM K J，HAGGLUND T.PID controllers：theory, design,，and tuning[M].1995,，1-55617-516-7.

[14] OGATA K.Discrete-time control systems(2nd ed.)[M].Prentice-Hall，Inc.,，1995.

[15] 趙成勇,，李路遙，翟曉萌,，等.新型模塊化高壓大功率DC-DC變換器[J].電力系統(tǒng)自動化,，2014，38(4)：72-78.

[16] OCAYA R O,，WIGDOROWITZ B.Application of finite state machines in hybrid simulation of dc-dc converters[C].Africon.IEEE,，2007：1-4.

[17] ZULUETA E，RICO T.Hybrid modeling of open loop DC-DC converters[J].Ingeniare Revista Chilena De Ingeniería,，2003,，11(2)：41-47.

[18] LI H，YE X. Sliding-mode PID control of DC-DC converter[C].2010 5th IEEE Conference on Industrial Electronics and Applications,，2010：730-734.

[19] 楊汝,，張波.DC-DC buck變換器時間延遲反饋混沌化控制[J].物理學報，2007,，56(7)：3789-3795.

[20] VISWANATHAN K,，SRINIVASAN D，ORUGANTI R.A universal fuzzy controller for a non-linear power electronic converter[C].IEEE International Conference on Fuzzy Systems,，2002.Fuzz-Ieee.IEEE,，2002：46-51.

作者信息:

吳志強，于蓮芝,，孔夢君

（上海理工大學 光電信息與計算機工程學院,，上海200093）