0 引言

    聲信號處理技術(shù)影響聲納系統(tǒng)對目標(biāo)的遠(yuǎn)程感知、探測,、定位以及識別的能力,，涉及的關(guān)鍵技術(shù)主要有方位估計(Direction of Arrival，DOA)^[1-3]和波束形成,。本文聚焦具有高分辨能力的DOA估計方法,，以期改善多目標(biāo)的檢測與跟蹤性能，從而進一步提高聲納系統(tǒng)的遠(yuǎn)程感知能力,。

    超分辨方位估計是指突破方位分辨瑞利限的一種方法,，子空間類算法是其中典型的超分辨方法之一,。子空間類算法主要通過對陣列輸出協(xié)方差矩陣進行特征值分解，以構(gòu)成相互正交的信號子空間和噪聲子空間,。子空間類算法通常分兩種：一種是以多重信號分類算法(MUltiple SIgnal Classification,，MUSIC)^[4]為典型代表的噪聲子空間算法，另一種是以旋轉(zhuǎn)不變子空間算法^[5-6](Estimation of Signal Parameter via Rotational Invariance Techniques,，ESPRIT)為典型代表的信號子空間算法,。MUSIC算法利用陣列流形向量與噪聲子空間的正交特性來實現(xiàn)超分辨方位估計，ESPRIT算法則利用數(shù)據(jù)協(xié)方差矩陣中信號子空間的旋轉(zhuǎn)不變特性給出目標(biāo)方位的估計值,，且ESPRIT算法計算量較MUSIC算法小,。

    由于MUSIC算法和ESPRIT算法在估計目標(biāo)方位時，均假設(shè)噪聲為加性白噪聲,，故噪聲協(xié)方差矩陣可以寫為噪聲方差與單位矩陣的乘積形式,。然而，各陣元接收的實際環(huán)境噪聲可能是相關(guān)的,，并且由于風(fēng)成噪聲和遠(yuǎn)處航船噪聲等因素的影響,，環(huán)境噪聲強度的空間分布也可能具有方向性^[7]。為此,，本文通過建立非均勻環(huán)境噪聲的信號處理模型,，引入稀疏譜擬合算法，提出了一種基于稀疏譜擬合的超分辨估計算法,，從而有效提高非均勻噪聲環(huán)境下的超分辨方位估計性能,。

1 非均勻環(huán)境噪聲模型

    考慮陣列流形為a(θ)∈C^M×1陣元個數(shù)為M的水聽器陣列接收K個遠(yuǎn)場窄帶入射信號，根據(jù)窄帶陣列信號處理模型,，在假設(shè)噪聲與信號不相關(guān)的條件下,，數(shù)據(jù)協(xié)方差矩陣表示為：

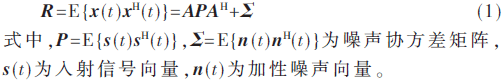
    通常認(rèn)為水聽器陣列的各陣元噪聲是互不相關(guān)的，一般假設(shè)n(t)為零均值的高斯白噪聲,，即E{n(t)n^H(t)}=σ²I,，σ²為噪聲方差。此假設(shè)模型對于電路系統(tǒng)的熱噪聲也適用,，然而在實際環(huán)境噪聲條件下,，各陣元接收到的環(huán)境噪聲可能是相關(guān)的，其空間分布也可能是不均勻的,。為了更加客觀地表示環(huán)境噪聲場信息,，通過使用線性噪聲模型(Linear Noise Model)^[8-9]，認(rèn)為環(huán)境噪聲是空間非均勻分布的噪聲場,，并假定噪聲強度是方位角θ的函數(shù),。

    給定采樣時間t，噪聲強度可看作是一個隨機變量v(θ,，t),。此時,，陣元接收噪聲波形為：

式中，

2 基于稀疏譜擬合的超分辨方位估計

    本節(jié)利用建立的非均勻環(huán)境噪聲模型,，引入稀疏譜擬合(Sparse Spectrum Fitting,，SpSF)算法，提出了一種基于稀疏譜擬合的超分辨方位估計算法,。

    假定空間非均勻環(huán)境噪聲條件下,，利用式(8)的線性噪聲模型，對式(11)兩邊進行矩陣向量化運算可得^[10]：

式中,，λ為正則因子,。

    由式(15)可知，DN-SpSF算法對環(huán)境噪聲信息進行參數(shù)化擬合,，進而實現(xiàn)方位估計,。

3 試驗驗證

3.1 DN-SpSF算法方位譜估計

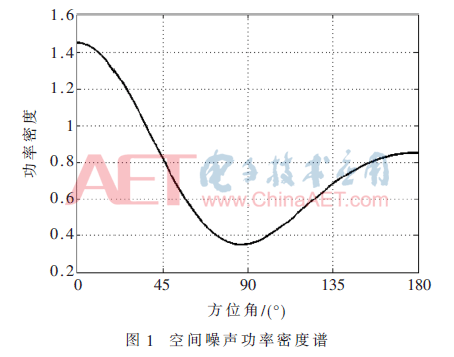
    考慮兩個遠(yuǎn)場窄帶信號分別從45°和90°入射到一個半波長間隔的10陣元均勻直線陣上，假定端射方向為0°與180°,，入射信號的功率均為0 dB，且入射信號間互不相關(guān),?？臻g噪聲功率密度函數(shù)ε(θ)如圖1所示，生成噪聲所用的模型階數(shù)為3階,，相應(yīng)的傅里葉級數(shù)展開系數(shù)為η=[1.5,，0，0.2,，0,，0.4，0,，0.1]^T,。總的快拍數(shù)等于陣元數(shù)的10倍,，即T=100,。SpSF和DN-SpSF兩種算法中，取正則參數(shù)λ為2,。觀測空間從0°變化到180°,，并以0.1°為步長間隔。也就是說,，掃描網(wǎng)格點數(shù)為Ω=1 801,，而信號個數(shù)為K=2，故Ω>>K,，滿足稀疏信號處理模型的條件,。仿真時信噪比為-10 dB,，DN-SpSF算法中使用的線性噪聲模型階數(shù)與生成噪聲所用模型階數(shù)都為3階。

    信噪比定義為第一個信號功率與參考陣元接收噪聲功率的比值,，即：

    對比了常規(guī)波束形成(Conventional Beamforming,，CBF)、SpSF和DN-SpSF三種估計算法,，相應(yīng)方位譜如圖2所示,。由圖可以看出，CBF算法由于受到非均勻環(huán)境噪聲的影響,，具有很高的旁瓣級,，且旁瓣走勢也與空間噪聲功率密度譜走勢一致。SpSF和DN-SpSF算法由于利用了信號模型的稀疏特性,，其方位估計性能明顯優(yōu)于CBF算法,，旁瓣級也被控制在更低的水平上。由于SpSF算法的旁瓣走勢也與空間噪聲功率密度譜走勢一致,，這導(dǎo)致方位譜估計的信號功率嚴(yán)重失真,。DN-SpSF算法利用了線性噪聲模型，故具有最低的旁瓣水平和最高的空間分辨能力,，空間噪聲功率密度譜的影響基本被屏蔽,。

3.2 正則參數(shù)λ對DN-SpSF的影響

    仿真條件同3.1，對SpSF和DN-SpSF算法進行Monte Carlo實驗,，正則參數(shù)取值范圍從0.5變化到3,，以0.1為步長間隔，獨立試驗次數(shù)200次,，信噪比0 dB,。

    DOA估計的均方根誤差(Root-Mean-Square Error，RMSE)定義為：

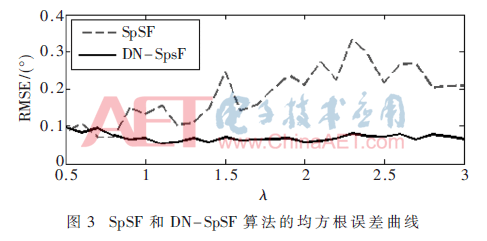
    圖3給出了SpSF和DN-SpSF算法在不同正則參數(shù)取值條件下方位估計的RMSE,?？梢钥闯觯诜蔷鶆颦h(huán)境噪聲背景條件下,，DN-SpSF算法較SpSF算法具有更低的RMSE,，且SpSF算法的RMSE值隨著正則參數(shù)的變化在很窄的數(shù)值范圍內(nèi)變動，說明DN-SpSF算法對正則參數(shù)的取值較SpSF算法更為穩(wěn)健,。

3.3 線性噪聲模型階數(shù)選取對DN-SpSF算法性能的影響

    仿真條件同3.1,，DN-SpSF算法所用的線性噪聲模型階數(shù)取值從1階連續(xù)增加到5階，同時分別在信噪比在0 dB和-5 dB條件下對DN-SpSF算法重復(fù)進行200次獨立試驗,，正則參數(shù)取為2,。

    選取不同線性噪聲模型的階數(shù)，并將相應(yīng)的RMSE列于表1中。當(dāng)DN-SpSF算法中使用線性噪聲模型階數(shù)的取值接近或者大于生成噪聲功率密度譜的階數(shù)（仿真時生成噪聲功率密度譜的階數(shù)為3階）時,，RMSE的值近似不變,，并且明顯小于1階噪聲模型的情況。正如式(9)和式(10)所示,，考慮到在實際感興趣的海洋環(huán)境中,，空間噪聲功率密度ε(θ)通常是一個隨著方位角θ緩慢變化的平滑函數(shù)，傅里葉級數(shù)展開的高階項系數(shù)近似為零,。因此,，傅里葉級數(shù)展開的低階項是影響噪聲空間譜擬合性能的關(guān)鍵因素，式(8)中線性噪聲模型的階數(shù)L通常為一個較小的數(shù)值,。在海上實驗數(shù)據(jù)處理時,，選取模型階數(shù)為5階，且認(rèn)為5階已足夠包含主要的低階傅里葉級數(shù)展開項,。

3.4 海上試驗驗證

    本小節(jié)使用DN-SpSF算法進行水下聲源的DOA估計,，并與傳統(tǒng)的CBF算法和SpSF算法進行對比，進一步說明了DN-SpSF算法在非均勻海洋環(huán)境條件下的方位估計性能,。

    海上試驗時,，進行水聲信號采集用的是一條32陣元的均勻線列陣，試驗季節(jié)在秋季,，試驗地點為南海某海域,。32陣元均勻線列陣的陣元間距為4 m，水平置于海面以下50 m處,。兩條實驗船分別記為A和B，在陣列的遠(yuǎn)場范圍沿著直線軌跡進行運動,，相應(yīng)的位置關(guān)系和運動軌跡示意圖如圖4所示,。

    觀測空間Θ=[0°，180°]以0.5°為步長間隔劃分掃描網(wǎng)格,，端射方向為0°和180°方向,。試驗數(shù)據(jù)處理時，關(guān)注的帶寬在100 Hz到200 Hz的低頻段,，采樣頻率為f_S=2 048 Hz,，快速傅里葉變換的點數(shù)取2 048個采樣點。整個數(shù)據(jù)時間長度取為60 min,，積分時間設(shè)為20 s,，每個積分時間內(nèi)數(shù)據(jù)被劃分為20個時間快拍，且使用50%作為快拍數(shù)據(jù)重疊率,。

    圖5中給出了算法CBF,、SpSF和DN-SpSF的時間方位歷程，其中DN-SpSF算法使用5階線性噪聲模型，SpSF和DN-SpSF算法的正則參數(shù)均為0.5,。兩艘實驗船軌跡和一些其他干擾均顯示在圖5(a)～圖5(c)中,。依據(jù)實驗船提供的GPS信息，實驗船A從大約150°的角度方向運動到180°的水聽器基陣端射方向,，然后接著運動到大約90°的正橫方向,。當(dāng)目標(biāo)出現(xiàn)在端射附近時，DOA的估計性能急劇下降,，這是由于在端射附近,，水聽器基陣的等效孔徑尺度將嚴(yán)重下降。與此同時,，實驗船B從大約60°方向運動到大約150°方向,，并且由近及遠(yuǎn)運動，相應(yīng)的目標(biāo)強度反映在空間譜圖的幅度上,。

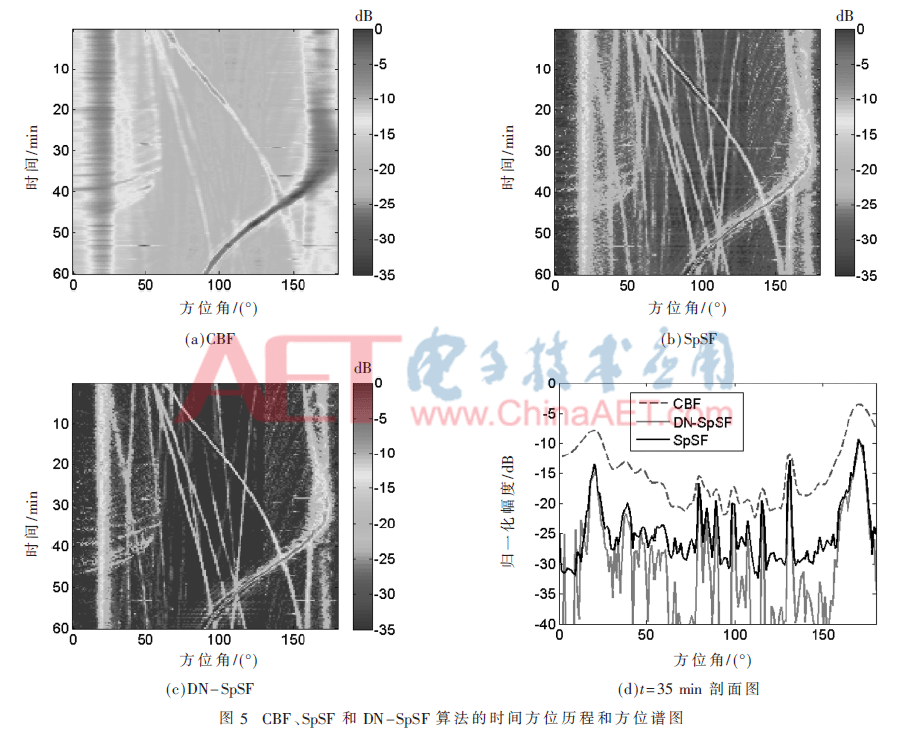
    如圖5所示,，由于利用了信號模型的稀疏性，SpSF和DN-SpSF算法的時間方位歷程圖明顯優(yōu)于CBF算法,。容易看出,，在前30 min的時間方位歷程圖上，SpSF和DN-SpSF算法估計的實驗船B的空間方位較CBF算法分辨能力更高,。然而,，實際的環(huán)境噪聲由于風(fēng)成噪聲和遠(yuǎn)處航船噪聲影響，通常是非均勻的,。如圖5(c)所示,，利用線性噪聲模型，DN-SpSF算法較SpSF算法可以獲得更低的旁瓣水平,。圖5(d)是上述算法在t=35 min時的方位譜圖,，DN-SpSF算法在實驗船A和B中間的空間角度范圍內(nèi)的平均旁瓣級為-36.7 dB，明顯小于SpSF算法的-28 dB,。同時,，圖5(d)中使用SpSF算法得到實驗船A和B的信號強度估計值分別為-12.86 dB和-9.42 dB；使用DN-SpSF算法得到實驗船A和B的信號強度估計值分別為-13.02 dB和-9.32 dB,。因此,，DN-SpSF算法可以獲得和SpSF算法估計信號強度一致的方位譜圖，并且DN-SpSF算法具有更低的旁瓣級,，這進一步驗證了DN-SpSF算法具有更好的環(huán)境適應(yīng)性,。

4 結(jié)論

    考慮到各陣元接收到的實際環(huán)境噪聲可能是相關(guān)的，并且由于風(fēng)成噪聲和遠(yuǎn)處航船噪聲等因素,，環(huán)境噪聲強度的空間分布也可能具有方向性,，因此本文提出了基于稀疏譜擬合的超分辨方位估計算法。該算法利用信號方位的稀疏性和線性噪聲模型擬合誤差的l1，l2范數(shù)聯(lián)合最小化實現(xiàn)非均勻環(huán)境噪聲條件下的超分辨方位估計,。仿真試驗討論了正則參數(shù)和線性噪聲模型階數(shù)對算法的性能影響,，海上試驗數(shù)據(jù)處理有效驗證了基于稀疏譜擬合的超分辨估計算法的性能。

參考文獻

[1] 唐建生.運動目標(biāo)輻射噪聲的寬帶波束形成研究[D].西安：西北工業(yè)大學(xué),，2006.

[2] 馮杰.穩(wěn)健波束形成與高分辨率方位估計技術(shù)研究[D].西安：西北工業(yè)大學(xué),，2006.

[3] 楊益新.聲吶波束形成與波束域高分辨方位估計技術(shù)研究[D].西安：西北工業(yè)大學(xué)，2002.

[4] SCHMIDT R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,，1986,，34(3)：276-280.

[5] ROY R，PAULRAJ A,，KAILATH T.ESPRIT-a subspace rotation approach to estimation of parameters of cisoids in noise[J].IEEE Transactions on Acoustics Speech & Signal Processing,，1986，34(5)：1340-1342.

[6] ROY R,，KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Transactions on Acoustics Speech & Signal Processing,，1989，37(7)：984-995.

[7] HAMSON R M.The modelling of ambient noise due to shipping and wind sources in complex environments[J].Applied.Acoustics,，1997,，51(3)：251-287.

[8] FRIEDLANDER B，WEISS A J.Direction finding using noise covariance modeling[J].IEEE Transactions on Signal Processing,，1995,，43(7)：1557-1567.

[9] OTTERSTEN B，STOICA P,，ROY R.Covariance matching estimation techniques for array signal processing applications[J].Digital Signal Processing,，1998，8(3)：185-210.

[10] YANG L,，YANG Y,，WANG Y.Sparse spatial spectral estimation in directional ambient noise environment[J].Journal of the Acoustical Society of America，2016,，140(3)：EL263-EL268.

作者信息:

郭曉明，吳姚振,，喬正明

（中國人民解放軍海洋環(huán)境保障基地籌建辦公室,，北京100088）