0 引言

    武器火控系統(tǒng)精度由火控系統(tǒng)和導(dǎo)彈制導(dǎo)系統(tǒng)兩個(gè)方面的精度組成,，慣導(dǎo)系統(tǒng)可以提供火控系統(tǒng)所需接收的導(dǎo)航信息，并且又是導(dǎo)彈制導(dǎo)系統(tǒng)的重要組成部分,，因而慣導(dǎo)系統(tǒng)的可靠性對保證火控系統(tǒng)的精度起著重要的作用,。慣導(dǎo)系統(tǒng)的可靠性主要取決于其中慣性儀表的可靠性，所以為了提高可靠性,，最早采用的方法是提高單個(gè)元器件的可靠性,，即設(shè)計(jì)具有大的平均無故障時(shí)間(MTBF)的元器件。這一方法要求更高的加工工藝及更好的加工材料,，并且對系統(tǒng)可靠性的提高極為有限。因此,，采用冗余技術(shù)^[1-11]使系統(tǒng)滿足可靠性的要求成為行之有效的方法,。這種高可靠性不是建立在嚴(yán)格要求元器件和生產(chǎn)工藝的質(zhì)量上，而是建立在“冗余”的設(shè)計(jì)上,，允許系統(tǒng)內(nèi)部存在故障,，通過容錯(cuò)設(shè)計(jì)消除故障的影響,，使系統(tǒng)仍能給出正確的結(jié)果。敖銀輝等人[1]對基于連續(xù)時(shí)間MDP模型的維護(hù)策略產(chǎn)出的效益進(jìn)行闡述,。本文通過結(jié)合MDP(Markov Decision Process)馬爾可夫決策過程算法理論的研究成果,，考慮所設(shè)計(jì)INU(Inerrtial Navigation Unit)慣性導(dǎo)航設(shè)備的可靠度與期望節(jié)約成本總體指標(biāo)意義下，采用霍華特(Howard)策略迭代法給出求解最優(yōu)INU冗余度的計(jì)算方法^[2],。

1 可靠度指標(biāo)及計(jì)算方法

    在可靠性理論中,，可靠度是指系統(tǒng)、元件等在規(guī)定的條件下和規(guī)定的時(shí)間內(nèi)正常工作的概率^[3-4],，記為R(t)或R₀(t),。

    文獻(xiàn)[3]指出，相對于INU而言,，配置結(jié)構(gòu)的最基本原則是線性不相關(guān),，即要求任意2個(gè)傳感器的測量軸不共線，任意3個(gè)傳感器的測量軸不共面,。從而,，對于INU中陀螺儀冗余配置，只要有3個(gè)以上單自由度陀螺儀能正常工作,，INU就能準(zhǔn)確輸出,。假設(shè)N個(gè)陀螺儀是同類型、統(tǒng)計(jì)獨(dú)立的,，而系統(tǒng)其他部件都是理想的,，可得N個(gè)單自由度陀螺儀冗余INU的可靠度R(t)為；

    由于安裝平臺復(fù)雜,，實(shí)際應(yīng)用中對INU需要定期檢測維修,，這里假設(shè)檢測維修時(shí)間間隔為0.5年，陀螺儀平均無故障時(shí)間(MTBF)為1萬小時(shí),，則根據(jù)式(3)可計(jì)算得到陀螺儀單元在維修間隔時(shí)間內(nèi)的可靠度為：

2 基于MDP的INU可靠度增強(qiáng)模型

2.1 MDP算法描述

    考慮MDP中最基本的離散時(shí)間馬爾可夫決策過程(DTMDP),。DTMDP考慮的是五元組^[12-13]：{S，A(i),，p_ij(a),，r(i，a),，V,，i，j∈S,，a∈A(i)},，各元的含義為：

    (1)S稱為系統(tǒng)的狀態(tài)空間，是系統(tǒng)所有可能的狀態(tài)所組成的非空狀態(tài)集,，它可以是有限的,、可列的或任意非空集,。

    (2)對狀態(tài)i∈S，A(i)是在狀態(tài)i處非空的可用的決策集,。

    (3)當(dāng)系統(tǒng)在決策時(shí)刻點(diǎn)t處于狀態(tài)i,，采取決策a∈A(i)時(shí)，則系統(tǒng)在下一決策時(shí)刻點(diǎn)t+1時(shí)處于狀態(tài)j的概率為p_ij(a),，它與決策時(shí)刻t無關(guān),。

    (4)當(dāng)系統(tǒng)在決策時(shí)刻點(diǎn)t處于狀態(tài)i，且采取決策a∈A(i)時(shí),，系統(tǒng)于本階段獲得的報(bào)酬為r(i,，a)。

    (5)V為準(zhǔn)則函數(shù),，也稱目標(biāo)函數(shù),。MDP常見的決策目標(biāo)函數(shù)有總報(bào)酬準(zhǔn)則、無限折扣準(zhǔn)則以及無限平均準(zhǔn)則等,。

    系統(tǒng)在t時(shí)刻的決策規(guī)則π_i是一概率分配函數(shù),，它決定可行決策集A(i)中各個(gè)決策取為實(shí)際決策a的概率，策略π是指一個(gè)決策規(guī)則列π={π_i},。文中采用MDP中常見的Markov策略^[6],。

2.2 MDP模型描述

    根據(jù)INU冗余結(jié)構(gòu)配置的特點(diǎn)，把考慮INU即時(shí)可靠度與期望節(jié)約成本總體指標(biāo)最大意義下最優(yōu)INU冗余度的整個(gè)選擇過程進(jìn)行狀態(tài)分解,，并表示為以下馬氏決策過程的參數(shù)形式：

    (1)決策時(shí)刻與周期

    前述分析中,，假設(shè)檢測維修時(shí)間間隔為0.5年，由于此檢測維修時(shí)間間隔已包含在單個(gè)陀螺儀的可靠度R₀(t)中,，因此可以無量綱時(shí)間t來描述,，如取t=0，1,，2,，…，且僅在這些時(shí)刻觀察系統(tǒng)的狀態(tài),。例如,，第一個(gè)階段所經(jīng)歷的時(shí)間為時(shí)間區(qū)間[0，1],。

    (2)狀態(tài)與決策集

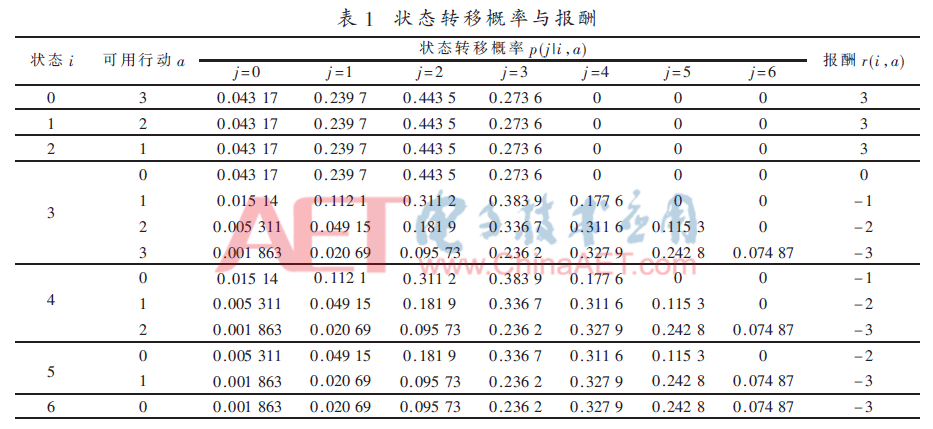
    INU冗余結(jié)構(gòu)中,，以在某一觀察時(shí)刻INU中正常工作的陀螺儀個(gè)數(shù)為狀態(tài)變量參數(shù)。設(shè)第k階段觀察到的所有可能狀態(tài)所組成的集合為X(k),，即X(k)={x₁(k),，x₂(k)，…，x_n(k)},，其中x_i(k)(i=0，1,，…,，6；k=1,，2,，…，∞)表示在第k階段初INU中處于正常工作狀態(tài)的陀螺儀個(gè)數(shù)i的期望值?，F(xiàn)有公開文獻(xiàn)中,，INU冗余結(jié)構(gòu)中單個(gè)自由度陀螺的最多冗余配置通常為5或6個(gè)^[7-8]，所以這里狀態(tài)選擇最大期望值為6,，所有期望狀態(tài)均列于表1,。

    在第k階段初始狀態(tài)為i時(shí)，所采取的決策記為a_k(i),，A_k={a_k(i)}為第k階段初始狀態(tài)為i時(shí)的決策集合,。令決策集A(i)={0，1,，2,，3}，即a_k(i)可選擇0,、1,、2、3,，分別表示在k時(shí)刻INU中增加0,、1、2,、3個(gè)冗余度,。

    狀態(tài)0的決策集為獨(dú)點(diǎn)集A(0)={3}，表示增加3個(gè)冗余度,，以使INU滿足系統(tǒng)準(zhǔn)確輸出的最低要求,；同理，狀態(tài)1的可用決策集為A(1)={2},，狀態(tài)2的可用決策集為A(2)={1},。狀態(tài)3的可用決策集A(3)={0，1,，2,，3}。為保證各時(shí)刻狀態(tài)i期望值不大于7，狀態(tài)4的可用決策集A(4)={0,，1,，2}，狀態(tài)5的可用決策集為A(5)={0,，1},，狀態(tài)6的可用決策集為A(6)={0}。

式中,，z為單個(gè)陀螺儀的代價(jià)權(quán)值,，表示增加陀螺將增加系統(tǒng)成本；P₀表示INU在檢測時(shí)間間隔內(nèi)能夠使系統(tǒng)準(zhǔn)確輸出的概率,，y為P₀的相應(yīng)報(bào)酬權(quán)值,。表1中給出了僅考慮期望節(jié)約成本的報(bào)酬取值。

    (4)目標(biāo)函數(shù)

    決策目標(biāo)函數(shù)定為無限階段折扣模型,，且折扣因子為β=0.9,。系統(tǒng)決策優(yōu)化準(zhǔn)則即是在滿足系統(tǒng)準(zhǔn)確輸出要求的前提下，使INU即時(shí)可靠度與期望節(jié)約成本總體指標(biāo)期望值最大^[12-13],。

3 試驗(yàn)分析性能評價(jià)

    策略迭代(policy iteration)算法也稱為策略空間逼近法,，它是求解折扣MDP的一個(gè)有效方法^[9-11]。策略迭代法分兩步進(jìn)行,，即策略求值與策略改進(jìn),。策略求值就是要求出最優(yōu)INU冗余度策略的一組相對值，策略改進(jìn)就是要確定每次迭代的最優(yōu)決策,。每個(gè)階段的最優(yōu)決策不斷迭代,，直到第k步與第k+1步迭代有A_k=A_k+1時(shí)計(jì)算結(jié)束，則A_k為最優(yōu)INU冗余度策略,，此時(shí)INU冗余度即為最低要求的INU冗余度,。

    假設(shè)INU冗余結(jié)構(gòu)中陀螺可靠度遵守二項(xiàng)分布，根據(jù)式(1),、式(4)可得在各狀態(tài)下采取不同決策的狀態(tài)轉(zhuǎn)移概率,，見表1。狀態(tài)轉(zhuǎn)移概率根據(jù)表1可以更加直接地了解決策選擇過程,。

    根據(jù)2.2節(jié)建立的模型,，利用策略迭代算法，編制了最優(yōu)INU冗余度選擇算法的MATLAB程序,。利用這個(gè)算法,，可對考慮INU即時(shí)可靠度與期望節(jié)約成本總體指標(biāo)意義下的目標(biāo)函數(shù)T(z，P₀)進(jìn)行求解,，計(jì)算出在不同的回報(bào)函數(shù)權(quán)值影響下,，應(yīng)該確定的系統(tǒng)最優(yōu)INU冗余度。下面通過實(shí)際驗(yàn)證證明本文提出的算法的合理性。

3.1 只考慮系統(tǒng)準(zhǔn)確輸出情況下的期望節(jié)約成本,，令y=0,，z=-1

    將表1中計(jì)算條件代入程序，得到策略迭代運(yùn)算結(jié)果如下：

    初始策略：F₁=[0 0 0 0 0 0 0]

    第一次迭代結(jié)果：F₂=[3 2 1 0 0 0 0]

    第二次迭代結(jié)果：F₃=[3 2 1 0 0 0 0]

    由計(jì)算知,，經(jīng)過2次迭代,，INU冗余度策略集合F₂=F₃，因此F^*=[3 2 1 0 0 0 0]是考慮INU期望節(jié)約成本意義下,，INU長期運(yùn)行下的最優(yōu)配置策略，即INU結(jié)構(gòu)中有3個(gè)陀螺儀,，恰好滿足系統(tǒng)準(zhǔn)確輸出最低要求,，驗(yàn)證了算法的合理性。

3.2 考慮INU即時(shí)可靠度與期望節(jié)約成本總體指標(biāo),，令y=100,，z=-1

    將計(jì)算條件代入程序，可以得到策略迭代運(yùn)算結(jié)果如下：

    初始策略：F₁=[0 0 0 0 0 0 0]

    第一次迭代結(jié)果：F₂=[3 2 1 1 0 0 0]

    第二次迭代結(jié)果：F₃=[3 2 1 1 0 0 0]

    由計(jì)算知,，經(jīng)過2次迭代,，INU冗余度策略集合F₂=F₃，因此F^*=[3 2 1 1 0 0 0]是考慮INU即時(shí)可靠度與期望節(jié)約成本總體指標(biāo)意義下,，INU長期運(yùn)行下的最優(yōu)配置策略,，即INU結(jié)構(gòu)中有4個(gè)陀螺儀。

    綜合上述兩種不同優(yōu)化指標(biāo),，可見提高INU可靠度要求后,，算法得出INU冗余結(jié)構(gòu)相對單純考慮成本指標(biāo)時(shí)須增加INU冗余度，從而算法可為INU冗余結(jié)構(gòu)設(shè)計(jì)提供合理的建議,。

4 結(jié)論

    本文在分析INU可靠度指標(biāo)和計(jì)算方法的基礎(chǔ)上,，構(gòu)建了INU冗余度馬氏決策控制模型，利用策略迭代算法進(jìn)行驗(yàn)證分析得出：基于INU即時(shí)可靠度與期望節(jié)約成本總體指標(biāo)或單獨(dú)指標(biāo)意義下,，運(yùn)用馬氏決策控制模型得出的最優(yōu)INU冗余度是節(jié)約成本最高或可靠度與期望節(jié)約成本總體指標(biāo)最高的,，且能夠滿足系統(tǒng)準(zhǔn)確輸出的要求。驗(yàn)證分析中的具體數(shù)據(jù)是通過實(shí)際情況真實(shí)獲得的,，因此用該模型計(jì)算出的結(jié)果具有較高的參考價(jià)值,，能夠?yàn)镾INS冗余可靠性設(shè)計(jì)提供建議。

參考文獻(xiàn)

[1] 敖銀輝,，王翠芬.基于連續(xù)時(shí)間MDP模型和隨機(jī)決策的維護(hù)周期[J].電子技術(shù)應(yīng)用,，2016，42(3)：123-126.

[2] 馮玎,，林圣,，張奧，等.基于連續(xù)時(shí)間馬爾可夫退化過程的牽引供電設(shè)備可靠性預(yù)測方法研究[J].中國電機(jī)工程學(xué)報(bào)，2017,，37(7)：1937-1946.

[3] 吳彩華,，馬建朝，魏海濤,，等.基于Markov鏈的軟件可靠性早期評估研究[J].空軍預(yù)警學(xué)院學(xué)報(bào),，2014，28(3)：199-202.

[4] 周圍正,，李學(xué)峰.單機(jī)五陀螺捷聯(lián)慣導(dǎo)系統(tǒng)重構(gòu)算法研究[J].航天控制,，2017，35(2)：3-7.

[5] 程建華,，董金魯.一種對稱斜置式四陀螺慣導(dǎo)冗余配置方案[J].傳感器與微系統(tǒng),，2015，34(2)：16-19,，27.

[6] 杜海東,，曹軍海，吳緯,，等.基于仿真的復(fù)雜系統(tǒng)可靠性冗余分配優(yōu)化設(shè)計(jì)[J].系統(tǒng)仿真學(xué)報(bào),，2016，28(3)：648-653.

[7] 王虎軍.冗余技術(shù)提高PLC控制系統(tǒng)可靠性的研究[J].計(jì)算機(jī)測量與控制,，2015,，23(12)：4016-4018.

[8] 李興偉，白博,，周軍.多模冗余可重構(gòu)計(jì)算機(jī)可靠性研究[J].計(jì)算機(jī)測量與控制,，2017，25(7)：309-312,，316.

[9] 張志偉.機(jī)載電子設(shè)備冗余設(shè)計(jì)與可靠性分析[J].光電技術(shù)應(yīng)用,，2017，32(3)：66-69.

[10] 劉玉寶,，秦貴和.面向可靠性冗余優(yōu)化的自適應(yīng)差分進(jìn)化算法[J].吉林大學(xué)學(xué)報(bào),，2016，54(1)：70-76.

[11] 王躍鋼,，楊家勝,，文超斌，等.一種針對冗余配置捷聯(lián)慣導(dǎo)的導(dǎo)彈初始對準(zhǔn)算法[J].導(dǎo)彈與航天運(yùn)載技術(shù),，2014(1)：65-69.

[12] 郁湧,，黃宇鑫，陳浩.基于構(gòu)件的可信軟件系統(tǒng)冗余機(jī)制及可靠性分析[J].計(jì)算機(jī)系統(tǒng)應(yīng)用,，2018,，27(1)：66-71.

[13] 王杜偉,，陶軍.基于半馬爾可夫過程容錯(cuò)導(dǎo)航系統(tǒng)可靠性分析的化簡[J].自動化與儀器儀表，2015(1)：154-156.

作者信息:

馮  楠1,，張  黎2

(1.92941部隊(duì)41分隊(duì),，遼寧 葫蘆島125000；2.61905部隊(duì),，遼寧 沈陽110000)