肖健,邵翠蘭
(廣東科技學(xué)院,廣東 東莞 523083)
摘要: 在信息論中,數(shù)據(jù)壓縮是數(shù)據(jù)處理的難題之一,尤其是圖像無(wú)損壓縮。JPEG-LS算法是公認(rèn)的灰度圖像有效的壓縮算法。然而,對(duì)于計(jì)算機(jī)繪制的灰度圖像(如CAD、SOLIDWORK等),其壓縮效率低,限制了JPEG-LS的廣泛應(yīng)用。提出一種基于兩步編碼法的圖像有效壓縮算法,即建模和編碼,算法與JPEG-LS灰度圖像壓縮標(biāo)準(zhǔn)進(jìn)行對(duì)比實(shí)驗(yàn),實(shí)驗(yàn)結(jié)果證明該算法提高了壓縮效率。
關(guān)鍵詞: 圖像壓縮;低熵源;預(yù)測(cè)誤差;圖像編碼;冗余度
0引言
數(shù)據(jù)壓縮是信息論的難題之一,解決方案有若干種[1],預(yù)測(cè)誤差編碼是圖像無(wú)損壓縮最常見(jiàn)的算法之一,基于這種思想算法總體方案可分為兩步:建模和編碼。使用類(lèi)圖像的模型,從上一數(shù)據(jù)預(yù)測(cè)該點(diǎn)的強(qiáng)度來(lái)計(jì)算有效圖像數(shù)據(jù)估計(jì)值。編碼步驟包括計(jì)算預(yù)測(cè)誤差,即實(shí)現(xiàn)與預(yù)測(cè)的強(qiáng)度差,壓縮采用二進(jìn)制表示。圖像壓縮方案首先使用日落算法實(shí)現(xiàn)[2],算法有多種變形,如單通道,其預(yù)測(cè)誤差和編碼一次完成;雙通道變型,先計(jì)算所有誤差,再進(jìn)行編碼[3]。對(duì)于灰度圖像,在算法復(fù)雜性和壓縮效率比率最佳方案公認(rèn)為是JPEGLS無(wú)損壓縮標(biāo)準(zhǔn)[4]。基于JPEGS標(biāo)準(zhǔn)算法進(jìn)行預(yù)測(cè)當(dāng)前點(diǎn)的強(qiáng)度,當(dāng)前點(diǎn)k是連續(xù)鄰接點(diǎn),用k比特?cái)?shù)表示(稱(chēng)為上下文),當(dāng)前點(diǎn)的強(qiáng)度、編碼的預(yù)測(cè)和編碼的整個(gè)過(guò)程可以分為三步[56]:
(1)計(jì)算當(dāng)前點(diǎn)的上下文,引用上一強(qiáng)度值(x);
(2)當(dāng)前點(diǎn)強(qiáng)度值()的預(yù)測(cè)源于上的值;
(3)ε=-x為計(jì)算預(yù)測(cè)誤差的概率模型參數(shù),使用步驟(1)和(2)及誤差編碼得到的數(shù)據(jù)。設(shè)誤差ε是兩邊幾何分布[56],關(guān)于某個(gè)對(duì)稱(chēng)值呈現(xiàn)指數(shù)衰減分布,概率模型分別用上下文表示,分布對(duì)稱(chēng)中心可以移動(dòng)使它接近于0[7]。
p(ε)=C(θ,d)θ|ε+d|(1)
當(dāng)ε=0,±1,±2…是預(yù)測(cè)誤差時(shí),參數(shù)取值范圍0<θ<1,0≤d≤1/2,其特征分布對(duì)稱(chēng)中心C(θ,d)歸一化因子由式(2)給出:

灰度圖像JPEG-LS壓縮算法優(yōu)于其他算法,然而對(duì)于計(jì)算繪制的灰度圖像,JPEG-LS算法效率低,限制了JPEG-LS的廣泛應(yīng)用。對(duì)于計(jì)算繪制的圖像,值為0時(shí)預(yù)測(cè)誤差ε的概率顯著高于照片圖像。ε使用RiceGolomb編碼對(duì)字符編碼[8]。在計(jì)算繪制圖像的情況下,其中一串零的概率足夠大,低熵源編碼算法是有效解決此類(lèi)型圖像的方案。
編碼低熵源算法已得到證明[8],它提供任意預(yù)定的冗余,同時(shí)保留編碼器和解碼器中一般方法相同的存儲(chǔ)器,算法的編碼和解碼率顯著提高[910]。
1預(yù)測(cè)誤差有效編碼算法
預(yù)測(cè)誤差構(gòu)造一個(gè)高效編碼算法,由一個(gè)低熵源貝努利源Sε與預(yù)測(cè)誤差值的字母表生成字符序列Aε={ε|ε∈[-n,n]},概率分布P(ε)由式(3)給出:
P(ε)=(1-θ)θε2θ,ε≠0;P(0)=1-θ(3)
式(3)是由式(1)和式(2)概率分布產(chǎn)生,令d=12(當(dāng)d=0和d=12時(shí),式(1)概率分布中心點(diǎn)為0[7])。考慮以上情況,實(shí)際上ε+dd,即令|ε+d|≈|ε|。
設(shè)
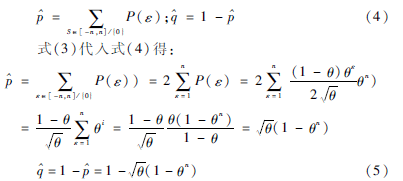
預(yù)測(cè)誤差ε序列編碼分為兩步驟:第1步,一個(gè)簡(jiǎn)單的代碼壓縮源生成消息,且作為結(jié)果輸出序列編碼在第2步中使用一個(gè)更復(fù)雜的代碼編碼。源是一個(gè)低熵源,在第1步之后,輸入序列長(zhǎng)度明顯減少,提供原始消息字符編碼的總時(shí)間減小。第2步,使用目前已知算法中最有效的算術(shù)編碼。考慮編碼的第1步,字符輸入序列劃分成長(zhǎng)度l=1/塊(子字符串),其中由式(4)給出。如果一個(gè)塊的誤差值僅有零值,則這個(gè)塊的編碼為0,如果一個(gè)塊包含誤差值至少有一個(gè)非零值(用k表示,-1≤|k|≤n),則該碼字長(zhǎng)度等于l+1:這個(gè)塊的開(kāi)頭碼字為某個(gè)特殊字符k,后跟相同塊長(zhǎng)度l。在這種情況下,第l+1在開(kāi)頭的碼字加字符k是有必要的,這表明在位于k后面長(zhǎng)度l塊中不可能是字符表觀。
例如,設(shè)A={0,1,2},P(0)=6/7,P(1)=2/21,P(2)=1/21,預(yù)測(cè)誤差序列的編碼為000000000001000 102000。
由式(4)得出=1/7,l=3的結(jié)果,編碼序列形式 000 1001 0 21020第1步編碼后得到序列,在編碼第1步之后,令z1z2…zs。(zi∈A,A={k|-n≤k≤n})。
第2步編碼是編碼算法,在序列z1z2…zs選擇長(zhǎng)度為l的塊后跟隨任意特殊字符k,特殊字符0和k不包含在塊中,序列z1z2…zs表示成:
0…0kz1…zll0…0kz′1…z′ll編碼方案描述如下:
特殊字符0和k(-n≤k≤n)由編碼器k0分別用l和1-l概率編碼,在式(4)中定義。
考慮長(zhǎng)度為l的塊z1z2…zs內(nèi)字符編碼,令z1…zi-1=0…0i-1(i=1,2,…,l),判斷字符zi的概率,位于第i個(gè)位置后i-1字符0的表觀,則有:
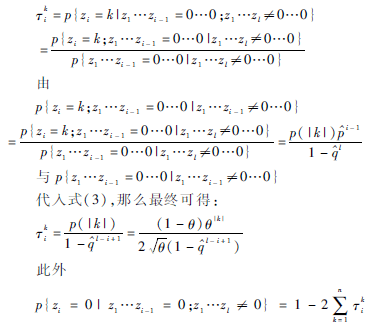
因此,塊z1…zl中,在第i位置字符zi之后出現(xiàn)i-1個(gè)零表觀,由編碼器Ki用概率Γki編碼,因?yàn)樽址鸎和1-2∑nk=1Γki為零。最后,塊中z1…zl字符位于任意字符k之后,由編碼器k^以初始概率和p(|k|)分別為0和k編碼[12],其中p(|k|)由式(3)給出。概率Γki不存儲(chǔ)在編碼器和解碼器之中,而是采用遞歸計(jì)算[1112]。首先,z1分別用字符0與k以Γk1和1-2∑nk=1τk1概率編碼,當(dāng)z1=k時(shí),則所有的字符接字符k以編碼器k^用初始概率p(|k|)和分別以k和0編碼。否則,計(jì)算Γk2,字符z2用Γk2和1-2∑nk=1τk2概率分別以k與0編碼[13]。因此,塊z1…zl中的字符編碼分為兩步執(zhí)行。
(1)計(jì)算Γki,字符zi用Γki和1-2∑nk=1τki概率編碼。
(2)如果zi=k,則所有的字符接zi以概率和p(|k|)編碼;否則,算法前移下一字符并返回到步驟(1)[1416]。
用遞推公式Γki計(jì)算:

下一塊的字符用相同方式編碼,編碼每一新塊之前用初始數(shù)據(jù)進(jìn)行更新。
使用之前步驟序列,考慮下面的編碼結(jié)構(gòu)。令:
p(0)==6/7
p(1)=2/21,p(2)=1/21,=1/7,l=3
編碼序列為:

這個(gè)序列表示為:
特殊字符使用編碼器k0用以下概率編碼
p(z1)=p(z2)=p(z3)=p(z8)=p(z13)=(6/7)3=216/343
p(z4)=p(z9)=1-(6/7)3=127/343
第1塊z5z6z7的字符串編碼如下。由式(6)可得:
![UO9(Z`BN%0IPZJ]E24JH8CC.jpg UO9(Z`BN%0IPZJ]E24JH8CC.jpg](http://files.chinaaet.com/images/2016/05/24/6359972520756200001672084.jpg)
所以,z7=1,由編碼器k3以τ13=2/3概率編碼。第2塊z10z11z12的字符串以相同的方式編碼。因?yàn)?τ11)-1=38198,z10=1也遵循編碼器k1以τ11=98/381概率編碼,余下的字符串z11和z12由編碼器k^以概率p(z11)=p(0)=6/7和p(z12)=p(2)=1/21編碼。編碼器與解碼器存儲(chǔ)大小以及所提出方法的編碼與解碼比率的特點(diǎn)在定理1中來(lái)描述[17]。
定理1設(shè)有一低熵源貝努利Sε,用字母表Aε={ε|ε[-n,n]}生成預(yù)測(cè)誤差序列,以概率分布p(ε)由式(3)和一些r(0<r<1)給出。第(1)步,令這個(gè)源用上述l=1/(<1/2)進(jìn)行編碼,其由式(4)給出。第(2)步,冗余r=r/2,總的冗余不超過(guò)r,并且編碼器與解碼器V(Sε)總的存儲(chǔ)器大小和一個(gè)符號(hào)T(Sε)編碼與解碼平均時(shí)間滿足不等式:
V<C1log1,T<C2·log(1r)·loglog(1r)·logloglog(1r)+C3
其中C1、C2和C3為常數(shù)。
證明:總編碼冗余量R=l′T。
l′=l1/l編碼是第1步之后獲得的代碼平均長(zhǎng)度(每個(gè)字符),當(dāng)僅有字符0組成的塊出現(xiàn),概率可表示為l=(1-)l,因此有:
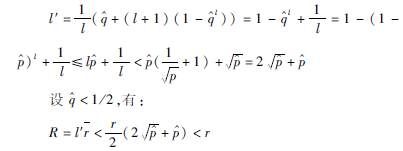
即總?cè)哂嗔坎怀^(guò)r。對(duì)該方法的平均編碼和解碼時(shí)間進(jìn)行評(píng)估,第(1)步序列字符壓縮編碼花費(fèi)時(shí)間等于

因此,計(jì)算量的時(shí)間Γki用在第(2)步不超過(guò)

乘以平均代碼長(zhǎng)度l′得第(2)步編碼的總時(shí)間,考慮第(1)步的時(shí)間等于0(1),發(fā)現(xiàn)對(duì)于所提出的方法,一個(gè)字符編碼和解碼平均時(shí)間滿足下式:

2算法實(shí)驗(yàn)結(jié)果
定理1給出了該方法有效性總體思想,然而更加實(shí)際意義是如何使所提出的方法對(duì)真實(shí)數(shù)據(jù)影響的問(wèn)題。用Waterloo Repertoire GreySet1標(biāo)準(zhǔn)圖像集對(duì)算法的性能進(jìn)行測(cè)試實(shí)驗(yàn),所有圖像尺寸為256×256像素,測(cè)試使用聯(lián)想PC的配置如下:CPU為IntelPentium(R) Dual-core,主頻為2 GHz,內(nèi)存2 GB,操作系統(tǒng)Windows 7。用JPEGLS標(biāo)準(zhǔn)對(duì)兩種算法進(jìn)行比較。表1和表2是兩種算法比較結(jié)果,圖像壓縮k(bit)和時(shí)間t(s)的程度要求編碼器來(lái)壓縮圖像,在這種情況下壓縮程度是指對(duì)應(yīng)于原圖像(未壓縮)中的一個(gè)字節(jié)(8 bit)的壓縮文件中的比特?cái)?shù)。換言之,如果L是原始文件的大小,L1是壓縮文件的大小,那么壓縮程度為8(L1/L)。一組計(jì)算機(jī)繪制圖像壓縮結(jié)果在表1中列出,另一組照片圖像壓縮數(shù)據(jù)在表2中列出。
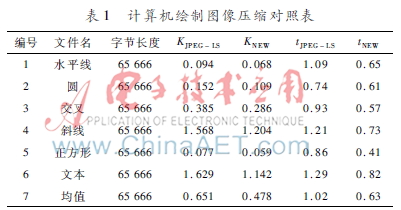
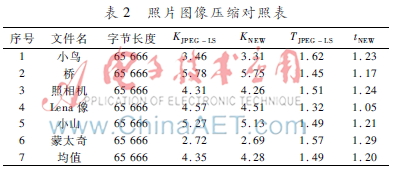
表1表明,計(jì)算機(jī)繪制圖像壓縮程度平均大于JPEGLS算法27%,編碼率提高約37%。對(duì)于照片圖像(如表2所示),新算法平均提高約2%,與JPEGLS算法相比,編碼率仍然較高,提高約21%。實(shí)驗(yàn)結(jié)果表明,算法提供了良好的壓縮比,證明所提出的算法是高效的。
3結(jié)論
本文所提出的基于兩步編碼有效算法經(jīng)實(shí)驗(yàn)證明,計(jì)算機(jī)繪制圖像編碼的壓縮比和編碼率明顯增加,分別提高27%和37%,超過(guò)JPEG算法。可應(yīng)用于地圖、地球表面的衛(wèi)星圖像和網(wǎng)頁(yè)圖形等實(shí)際領(lǐng)域。對(duì)于固定位置和固定數(shù)目的像素進(jìn)行預(yù)測(cè)公式較簡(jiǎn)單,預(yù)測(cè)的像素點(diǎn)能充分利用。
參考文獻(xiàn)
[1] TROFIMOV V K. Efficiency of outputuniform coding of bernoulli sources for unknown message statistics[J]. Avtometriya, 2010,46(6):3239.
[2] TODD S, LANGDON G. G, RISSANEN J. Parameter reduction and context selection for compression of the grayscale images[J]. IBM J. Res. Develop, 2013,29(2):188193.
[3] HOWARD P G, VITTER J S. Fast and efficient lossless image compression[C]. In Proc. IEEE Data Compression Conference, Snowbird, Utah, 2012: 351360.
[4] WEINBERGER M J, SEROUSSI G, SAPIRO G. The LOCOI lossless image compression algorithm: principles and standardization into JPEGLS[J]. IEEE Transacation on Image Process, 2013,9(8):13101324.
[5] NETRAVALI A, LIMB J O. Picture coding: a review[J]. Proceedings of the IEEE 1980,68(3): 366406.
[6] REININGER R C, GIBSON J D. Distributions of the twodimentional DCT coefficients for images[J]. IEEE Transacations on Communicatons, 2013,31(6):835839.
[7] MERHAV N, SEROUSSI G, WEINBERGER M J. Optimal prefix codes for sources with twosided geometric distributions[J]. IEEE Transacations on Information Theory, 2013,46(1):121135.
[8] RYABKO B J, SHAROVA M P. Fast coding of lowentropy sources[J]. Probl. Peredachi Information, 2010,35(1): 4961.
[9] RYABKO YA B, FIONOV A N. Homophonic coding with logarithmic memory size[M]. In Algorithms and Computation, Springer, Berlin, 2009:253262.
[10] WITTEN I H, NEAL R M, CLEARY J G. Arithmetic coding for data compression communication[J]. ACM, 1987,30(6):520540.
[11]Library of images for testing and demonstration of data compression algorithms[EB/OL].[20120112](20160105). http://cdb.paradiceinsight.us/corpora/Corpus% 20Waterloo/GreySet1/?C= N;O=A.
[12] 王鳳, 萬(wàn)智萍. 基于閾值與人眼特性的小波圖像壓縮算法[J]. 圖學(xué)學(xué)報(bào), 2013,34(6): 8086.
[13] 褚靜, 徐安成, 張美鳳. 基于DWTLSSVM的圖像壓縮算法[J]. 計(jì)算機(jī)工程與應(yīng)用, 2013,40(14):156159.
[14] 楊曉,劉俊杰, 楊學(xué)友.基于ROI編碼的任意尺寸測(cè)量圖像的壓縮方法[J]. 計(jì)算機(jī)工程與應(yīng)用,2013,40(4): 1417.
[15] 陽(yáng)婷,官洪運(yùn),章文康,等. 基于小波變換的圖像壓縮算法的改進(jìn)[J]. 計(jì)算機(jī)與現(xiàn)代化, 2014,40(10):123126.
[16] 田馳.小波Contourlet變換圖像壓縮算法[J]. 長(zhǎng)春工業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版) , 2014,40(4):8991.
[17] 陳鴻,柏森,劉博文.混沌和小波變換的圖像加密壓縮算法[J]. 重慶大學(xué)學(xué)報(bào), 2014,40(6):6570.

