0  引言

    在如今清潔能源尤其是風(fēng)力發(fā)電大規(guī)模發(fā)展的大背景下,，風(fēng)力發(fā)電的建模問(wèn)題十分重要^[1-2]。但在平臺(tái)上實(shí)現(xiàn)每臺(tái)風(fēng)機(jī)的詳細(xì)建模,，不僅在電網(wǎng)的角度考慮沒(méi)有必要,，而且會(huì)帶來(lái)非常巨大的計(jì)算與任務(wù)量。因此,，等值建模在風(fēng)電場(chǎng)并網(wǎng)研究甚至在整個(gè)風(fēng)力發(fā)電中都是十分重要的,。風(fēng)電場(chǎng)的建模分為穩(wěn)態(tài)建模和動(dòng)態(tài)建模，考慮到風(fēng)能的特性以及我們所需求的前提下,，動(dòng)態(tài)建模更加符合要求,。其中，聚合法又是動(dòng)態(tài)建模的有效解決方法,。

    文獻(xiàn)[3]提出用單機(jī)表征法對(duì)風(fēng)電場(chǎng)進(jìn)行等值建模,，但是在對(duì)風(fēng)電場(chǎng)的并網(wǎng)運(yùn)行時(shí)，因?yàn)轱L(fēng)電場(chǎng)內(nèi)部的風(fēng)速差異以及其他的因素,，單機(jī)表征法會(huì)產(chǎn)生較大的誤差,。文獻(xiàn)[4]用風(fēng)機(jī)機(jī)組簡(jiǎn)化模型進(jìn)行風(fēng)電場(chǎng)等值，以風(fēng)能利用系數(shù)為指標(biāo)將發(fā)電機(jī)轉(zhuǎn)速-功率特性線性化處理,。但由于等值過(guò)程中做了若干假設(shè)和忽略處理,，模型的精度不夠。文獻(xiàn)[5]在研究風(fēng)電場(chǎng)等值建模時(shí),，只考慮了等效風(fēng)速,。然后根據(jù)等效風(fēng)速求得風(fēng)電場(chǎng)輸出。文獻(xiàn)[6]則是基于PQ節(jié)點(diǎn)法,，將風(fēng)電場(chǎng)先分群后進(jìn)行潮流計(jì)算,。

    本文針對(duì)大型機(jī)組風(fēng)電場(chǎng)，在動(dòng)態(tài)建模和聚合法的前提下提出一種應(yīng)用改進(jìn)的猴群算法的風(fēng)電場(chǎng)等值建模方法,，并在DIgSILENT軟件平臺(tái)進(jìn)行仿真驗(yàn)證,，仿真結(jié)果證明了該方法的有效性。

1  風(fēng)電場(chǎng)的單機(jī)模型

    單單針對(duì)一臺(tái)風(fēng)力發(fā)電機(jī)而言,，基本的參數(shù)應(yīng)該包括的參數(shù)有發(fā)電機(jī)的容量,、輸入發(fā)電機(jī)的機(jī)械轉(zhuǎn)矩、定子轉(zhuǎn)子電阻電抗,、勵(lì)磁電抗以及慣性時(shí)間常數(shù)等參數(shù),。

    其中，定子電阻電抗,、轉(zhuǎn)子電阻電抗,、勵(lì)磁電抗可以通過(guò)改進(jìn)的猴群算法求得。

    風(fēng)電機(jī)組的容量和輸入機(jī)械功率可以根據(jù)容量加權(quán)平均值求得,。如式（1）所示：

    其中S_eq為等值的風(fēng)電機(jī)組的容量,，P_meq為風(fēng)電機(jī)組的輸入機(jī)械功率,。S_i則表示第i臺(tái)風(fēng)電機(jī)組的容量，P_mi則表示第i臺(tái)風(fēng)電機(jī)組的輸入機(jī)械功率,。

    其他的參數(shù)可由猴群算法求得,。

2  猴群算法簡(jiǎn)介

    猴群算法的主要用于解決含有連續(xù)變量的大規(guī)模、多峰值函數(shù)優(yōu)化問(wèn)題,屬于風(fēng)電場(chǎng)建模的聚合法中的辨識(shí)法,。

    猴群算法顧名思義,，就是再現(xiàn)猴群不斷地爬向更高的山峰，直到山頂?shù)倪^(guò)程,。它是由爬,、望、跳,、翻四部分組成,。大體流程為爬—望—跳—爬—翻—爬的過(guò)程。整個(gè)過(guò)程中爬就是算法的最主要工作,，主要用于計(jì)算局部最優(yōu)的參數(shù),。望的過(guò)程則是在接近最優(yōu)解的時(shí)候選定目標(biāo)加快計(jì)算過(guò)程，翻則是為了跳出局部最優(yōu)解的束縛,。在高緯度的優(yōu)化算法中,，因?yàn)楹锶核惴ǖ淖陨淼奶匦裕蛊淇梢源蟠蟮募涌焖惴ǖ氖諗克俣取?/p>

    傳統(tǒng)猴群算法的流程圖如圖1所示,。

2.1  爬過(guò)程

    爬過(guò)程對(duì)應(yīng)的機(jī)理為不斷的改善自身，使自身不?？拷繕?biāo)函數(shù)的過(guò)程,。具體流程為：

    （1）以一定步長(zhǎng)a的對(duì)初始參數(shù)每一項(xiàng)進(jìn)行擾動(dòng)，擾動(dòng)量為：

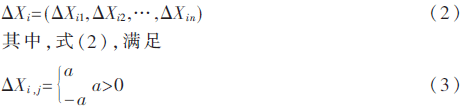
    步長(zhǎng)a的正負(fù)取值都為0.5的概率,。從擾動(dòng)能看出,，a的大小決定了猴群求取參數(shù)的時(shí)間。

    （2）計(jì)算偽梯度向量：

    （3）利用偽梯度找到猴子的新位置,。

    （4）帶入目標(biāo)函數(shù)進(jìn)行檢驗(yàn),，若新的位置產(chǎn)生的目標(biāo)函數(shù)滿足要求，則用新的參數(shù)代替上一步參數(shù),。若不滿足要求則保持上一步的參數(shù)不變,。

    （5）重復(fù)上面的步驟，直到達(dá)到迭代的最大次數(shù)或者兩次迭代之間的目標(biāo)函數(shù)相差到達(dá)設(shè)定的閾值,。

2.2  望的過(guò)程

    在爬的過(guò)程中,，每個(gè)元素都達(dá)到了暫時(shí)的局部最優(yōu)。此時(shí),，需要觀察周圍的向量空間,，是否有更優(yōu)解,。此處定義b作為猴群機(jī)參數(shù)的視野范圍。具體過(guò)程為：

    （1）針對(duì)參數(shù)xij在視野范圍內(nèi)隨機(jī)選取相鄰點(diǎn)并進(jìn)行計(jì)算,。生成一個(gè)新的參數(shù)y_ij,。

    （2）若y_ij滿足約束條件，且更加符合要求,，則令y取代x_ij,。否則重復(fù)計(jì)算到一定次數(shù)或找到滿意的y_ij。

    （3）用y_ij作為初始位置,，重塑2.1的過(guò)程,。

2.3  跳的過(guò)程

    該過(guò)程的目的為將整體的運(yùn)算由當(dāng)前的區(qū)域整體跳躍到新的區(qū)域。此時(shí)需要選取所有參數(shù)的重心作為支點(diǎn),。每個(gè)參數(shù)都沿當(dāng)前位置指向指點(diǎn)位置進(jìn)行跳躍,。具體過(guò)程為：

    （1）在區(qū)間[c，d]上生成一個(gè)隨機(jī)的實(shí)數(shù)θ,；

    確定新的參數(shù)y =（y₁,，y₂，…,y_n）,，若新的參數(shù)滿足要求,，則替換y為新的參數(shù)。若不滿足要求,，則重復(fù)計(jì)算直到達(dá)到最大的計(jì)算次數(shù)或者找到滿足要求的y,。

3  猴群算法的改進(jìn)

    本文針對(duì)風(fēng)電場(chǎng)的建模問(wèn)題，結(jié)合了混沌算法做出了一些改進(jìn),。

3.1  初始參數(shù)的改進(jìn)

    針對(duì)傳統(tǒng)初始化的繁瑣,，本文提出了混沌的方法來(lái)確定初始位置，采取了Logistic函數(shù)以便于加快參數(shù)的初始化過(guò)程,。其中Logistic函數(shù)的表達(dá)如式（7）所示：

    其中,，y混沌變量，k為迭代次數(shù),。

    Logistic函數(shù)在猴群算法的引用是為代替之前的設(shè)置：

    （1）設(shè)置k=0時(shí)y的初始值,；

    （2）帶入式（7）利用函數(shù)產(chǎn)生下一次的迭代變量值；

    （3）利用函數(shù)的迭代值帶入?yún)?shù)的尋優(yōu)過(guò)程,；

    （4）直到達(dá)到最大的迭代次數(shù)或者數(shù)值符合要求,，否則，返回步驟（2）,。

3.2  爬的過(guò)程改進(jìn)

    在爬的過(guò)程,，引入Sigmoid函數(shù)代替原來(lái)的定步長(zhǎng)的過(guò)程。Sigmoid的函數(shù)表達(dá)為:

    目的是在算法的不斷推進(jìn)中,，步長(zhǎng)需要從大到小的遞減,，這樣才能保證求參數(shù)的精度和時(shí)間優(yōu)化,。

    引進(jìn)函數(shù)替代了原來(lái)固定步長(zhǎng)的設(shè)置，伴隨著迭代次數(shù)的增加,，步長(zhǎng)逐漸縮小,。減少最開(kāi)始的求解時(shí)的時(shí)間，在保證結(jié)果的前提下,，提高了搜索的效率,。

4  算例驗(yàn)證

4.1  參數(shù)獲取

    本次的仿真采用60×1.5 MW的風(fēng)電場(chǎng)，其位于平坦地形排列規(guī)律且風(fēng)電場(chǎng)內(nèi)均為同一型號(hào)的雙饋風(fēng)電機(jī)組,。在DIgSILENT仿真平臺(tái)上進(jìn)行仿真建模,。為風(fēng)電場(chǎng)的結(jié)構(gòu)示意圖如圖2所示。

    風(fēng)電場(chǎng)的等值模型如圖3所示,，其中,，ExternaGrid代表風(fēng)電場(chǎng)外部的等值電網(wǎng)，PCC與PC分別代表風(fēng)電場(chǎng)主變壓器Trf_eq高壓側(cè),，低壓側(cè)與外電網(wǎng)連接的母線,。

    對(duì)于最終等值的模型，其額定容量為：

    其中,，ρ_AIR是空氣密度,，單位kg/m³；R為風(fēng)葉半徑（單位為m）,；V_i為風(fēng)電場(chǎng)中i臺(tái)風(fēng)機(jī)所捕獲的有效風(fēng)速（單位為m/s）,；C_Pi為i臺(tái)風(fēng)機(jī)的風(fēng)能利用系數(shù)。

    風(fēng)電場(chǎng)中雙饋機(jī)組的詳細(xì)參數(shù)如表1所示,。

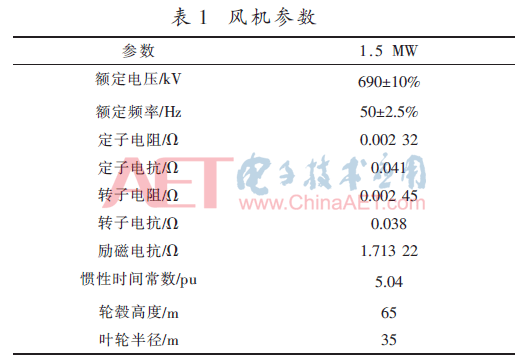
    在仿真時(shí),，根據(jù)風(fēng)況的分類結(jié)構(gòu)圖如圖3所示，先針對(duì)相同風(fēng)況的每列風(fēng)機(jī)參數(shù)利用式加權(quán)平均值進(jìn)行計(jì)算,，其后根據(jù)算法對(duì)給出的風(fēng)機(jī)參數(shù)求取猴群算法的初始參數(shù),，初始參數(shù)如表2所示,。

    根據(jù)表2中的參數(shù),，在初始參數(shù)的基礎(chǔ)上，上下50%作為搜索范圍,。參數(shù)如表3所示,。

    最后在表3所給范圍中，利用改進(jìn)的猴群算法與所給出的目標(biāo)函數(shù)來(lái)計(jì)算所得最優(yōu)參數(shù)如表4所示,，利用表4的數(shù)據(jù)完善風(fēng)電場(chǎng)的等值模型,。

4.2  仿真驗(yàn)證分析

    將仿真模型帶入不同時(shí)間段的兩組時(shí)長(zhǎng)為120 s的風(fēng)電場(chǎng)數(shù)據(jù)，用來(lái)驗(yàn)證等值模型的有效性,。

    在標(biāo)準(zhǔn)偏差為1.8的風(fēng)速如圖4所示,。其中,，橫坐標(biāo)為時(shí)間，縱坐標(biāo)為風(fēng)速,。

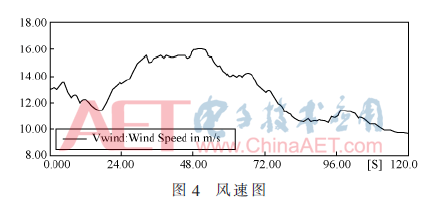
    在標(biāo)準(zhǔn)偏差下的風(fēng)電場(chǎng)等值前后的有功輸出對(duì)比圖如圖5所示,。橫坐標(biāo)為時(shí)間，縱坐標(biāo)為輸出的功率,。虛線所代表為詳細(xì)的風(fēng)電場(chǎng)模型輸出功率曲線,，實(shí)線為等值風(fēng)電場(chǎng)的輸出曲線。

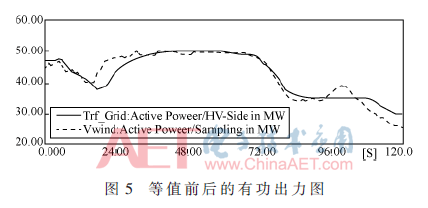
    在風(fēng)速偏差為0.45時(shí),，取120 s風(fēng)速波動(dòng)圖,，如圖6所示。在同風(fēng)速下的風(fēng)電場(chǎng)等值前后輸出對(duì)比圖如圖7所示,。

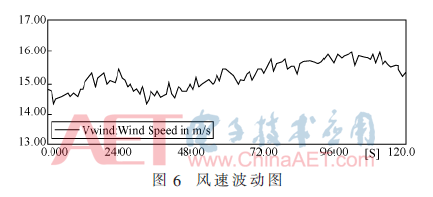
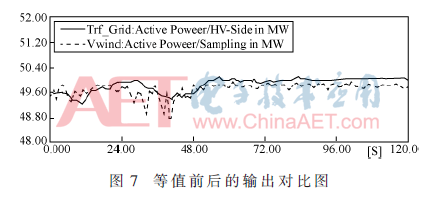
    從上圖可以看出,，在改進(jìn)猴群算法的前提下，所建等值模型的輸出特性與詳細(xì)模型基本吻合,，這驗(yàn)證了本文提出的等值建模的有效性,。

    在利用猴群算法迭代參數(shù)時(shí)，最終的參數(shù)相差不大,。但是迭代的時(shí)間上,，傳統(tǒng)的猴群算法消耗時(shí)間幾乎為改進(jìn)的猴群算法的二倍。這也說(shuō)明了改進(jìn)的猴群算法可以在保證結(jié)果精度的前提下,，提高運(yùn)算的效率,。

5 結(jié)論

    本次研究在原有的猴群算法的基礎(chǔ)上，結(jié)合混沌算法對(duì)傳統(tǒng)的算法的初始化和爬的過(guò)程針對(duì)性的修改,，進(jìn)行了大型雙饋機(jī)組風(fēng)電場(chǎng)等值建模的研究,。在研究中分析了傳統(tǒng)單機(jī)等值方法的不足以及等值前后下的仿真分析對(duì)比。

    從仿真的結(jié)果可以看出,，本次研究的方法與傳統(tǒng)的猴群算法相比更加符合風(fēng)電場(chǎng)的特性,。為大型風(fēng)電場(chǎng)的并網(wǎng)提供了基礎(chǔ)。

參考文獻(xiàn)

[1] 李輝, 王荷生, 史旭陽(yáng),等. 基于遺傳算法的風(fēng)電場(chǎng)等值模型的研究[J]. 電力系統(tǒng)保護(hù)與控制, 2011, 39(11):1-8.

[2] 喬嘉賡, 魯宗相, 閔勇,等. 風(fēng)電場(chǎng)并網(wǎng)的新型實(shí)用等效方法[J]. 電工技術(shù)學(xué)報(bào), 2009, 24(4):209-213.

[3] 黃梅, 萬(wàn)航羽. 在動(dòng)態(tài)仿真中風(fēng)電場(chǎng)模型的簡(jiǎn)化[J]. 電工技術(shù)學(xué)報(bào), 2009, 24(9):147-152.

[4] 嚴(yán)干貴, 李鴻博, 穆鋼,等. 基于等效風(fēng)速的風(fēng)電場(chǎng)等值建模[J]. 東北電力大學(xué)學(xué)報(bào), 2011, 31(3):13-19.

[5] 王偉勝, 申洪. 電力系統(tǒng)潮流計(jì)算中風(fēng)電場(chǎng)節(jié)點(diǎn)的考慮方法[J]. 華北電力大學(xué)學(xué)報(bào)(自然科學(xué)版), 2002, 29(s1):150-153.

[6] 張保會(huì), 李光輝, 王進(jìn),等. 風(fēng)電接入對(duì)繼電保護(hù)的影響(二)——雙饋式風(fēng)電場(chǎng)電磁暫態(tài)等值建模研究[J]. 電力自動(dòng)化設(shè)備, 2013, 33(2):1-7.

[7] 張新燕, 王維慶, 何山. 風(fēng)電并網(wǎng)運(yùn)行與維護(hù)[M]. 北京: 機(jī)械工業(yè)出版社, 2011.

[8] 鄭睿敏, 李建華, 李作紅,等. 考慮尾流效應(yīng)的風(fēng)電場(chǎng)建模以及隨機(jī)潮流計(jì)算[J]. 西安交通大學(xué)學(xué)報(bào), 2008, 42(12):1515-1520.

[9] 楊揚(yáng). 風(fēng)電場(chǎng)等值建模研究[D]. 濟(jì)南: 山東大學(xué), 2016.

[10] 陳海濤. 改進(jìn)的猴群算法在云計(jì)算資源分配中的研究[J]. 計(jì)算機(jī)系統(tǒng)應(yīng)用, 2015, 24(8):191-196.

作者信息:

王旭東,，董建園

（西安建筑科技大學(xué) 機(jī)電工程學(xué)院,，陜西 西安 710055）