0 引言

    當今導航定位領域，使用慣性導航系統(tǒng)(Inertial Navigation System,，INS)+里程計(Odometry，OD)+高程計的組合定位方式進行定位是主流的自主定位手段,，但是該系統(tǒng)本身存在的誤差會隨著時間不斷發(fā)散,，需要靠其他傳感器來進行輔助定位。三維點云激光雷達定位作為一個新興的手段,，具有不受光線影響,、分辨率高、測量距離遠的優(yōu)點,。激光雷達和慣性導航進行組合的定位方式也是當今實現(xiàn)無人駕駛的主流技術途徑之一,。為了滿足該系統(tǒng)的定位精度，傳感器之間的參數(shù)標定至關重要,，參數(shù)標定精度直接影響融合定位結果,。

    最初，激光雷達主要利用外部的經緯儀和測距儀直接進行輪廓測量^[1],，以此得到標定參數(shù),，但是這種方法過于繁瑣且精度較低。目前已經提出了多種針對激光雷達位姿的標定方法,。程金龍^[2]采用三面靶標的激光雷達外參數(shù)標定的方法,，使用隨機采樣一致性算法完成了平面分割和同名向量的提取，最后解出標定參數(shù),；韓正勇^[3]提出了一種可以在采樣幀數(shù)比較少的情況下獲得較高精度的參數(shù)矩陣的方法,，該方法采用棋盤面對應性的性質,，將坐標系標定問題轉換為三維空間中旋轉和縮放矩陣的求解問題；韓棟斌^[4]提出了一種在非理想?yún)?shù)初值的條件下依然可以獲得較好標定結果的方法,，該方法采用多對點云同時匹配迭代生成外參數(shù)來進行參數(shù)解算,。

    最小二乘法作為處理空間坐標組合轉換的經典方法之一，被廣泛應用于多種傳感器的系統(tǒng)坐標標定^[5-8],。針對最小二乘法標定的改進也在不斷進行^[9],。趙立峰^[10]將整體最小二乘法引入了坐標轉換中，提出了一種迭代算法,，降低低精度點的影響,；楊仕平^[11]提出在標志點數(shù)目在4個及以上，且在兩套坐標系下均存在隨機誤差的情況下,，采用多元整體最小二乘法進行解算,，提高算法精度。

    隨著即時定位與地圖構建(Simultaneous Localization and Mapping,，SLAM)技術的發(fā)展,，基于3D點云匹配技術的點云拼接方法日趨成熟，3D點云匹配的思路可以運用到坐標系標定的問題中,，通過點云匹配方法求解兩個坐標系的坐標轉換矩陣,。常用的3D點云匹配方法有ICP、正態(tài)分布變換(Normal Distributions Transform,，NDT)等算法,。點云配準方法有很多種，目前比較普遍的處理方式是基于點-點匹配的迭代最近點方法(ICP),、進一步提取特征進行特征匹配的改進ICP算法以及采用概率模型描述點云正態(tài)分布的NDT算法^[12],。原始的ICP算法由Besl等提出^[13]，核心思想為計算使得匹配點對歐氏距離和最小的坐標變換矩陣,。針對常規(guī)ICP算法的缺陷,，國內外的學者也提出了大量的改進算法，如MINGUEZ J^[14]提出了一種新的距離尺度函數(shù),，同時考慮到平移和選轉,，解決了旋轉誤差的問題。NDT算法是BIBER P^[15]提出的,，這種算法完全基于概率模型進行匹配,。

    本文中將提出一種基于點云匹配思想的車載激光雷達/IMU聯(lián)合標定的方法，并與基于最小二乘法的標定結果進行對比,。

1 基本原理

    激光雷達與IMU之間存在安裝誤差角和位置誤差,，因此兩個傳感器測量得到的同一組標志點的三維坐標不同，可以通過對應坐標點的關系來計算得到坐標系之間的轉換矩陣，完成激光雷達/IMU坐標系的聯(lián)合標定,。

    兩坐標系下三維坐標的關系模型如圖1所示,。

    (oX₁Y₁Z₁)為坐標系M，(OX₂Y₂Z₂)為坐標系N,，標志點在兩個坐標系之間的坐標分別為(x₁,，y₁，z₁),、(x₂,，y₂，z₂),，兩者之間的坐標變換矩陣為T_3D為4×4矩陣,，由旋轉矩陣R和平移矩陣T組成。

    坐標系N相對坐標系M的歐拉角為俯仰角θ,、橫滾角γ,、方位角Ψ，相對于軸向的平移量為t_x,、t_y,、t_z，則：

2 標定方案

2.1 總體方案

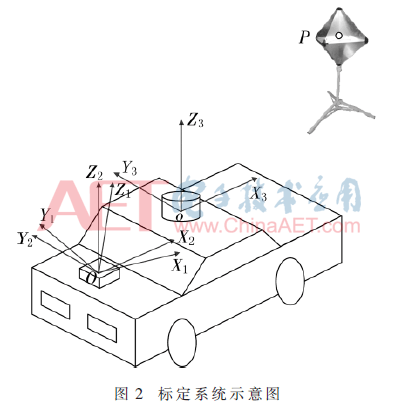
    本文采用具有多面反射,、反射強度高,、高度可調等優(yōu)點的角反射器作為標志物，通過移動角反射器可獲得在雷達坐標系下標志物在不同位置的坐標,，并同時采用差分GPS獲得標志物在當前位置的地理坐標系下的坐標,。因標定場地不水平，通過車載IMU測得車輛相對地理坐標系的姿態(tài)角及IMU處的地理坐標系坐標,，通過坐標變換將標志物在地理坐標系下的坐標轉換到IMU坐標系下。坐標系描述如下：地理坐標系為(OX₁Y₁Z₁),，IMU坐標系為(OX₂Y₂Z₂),，激光雷達坐標系為(oX₃Y₃Z₃)。標定系統(tǒng)總體方案示意圖如圖2所示,。

    IMU和激光雷達坐標系的參數(shù)標定流程如圖3所示,，標定步驟如下：

    (1)采集地理坐標系標志點的原始數(shù)據(jù)和激光雷達坐標系下的點云數(shù)據(jù)。

    (2)因為IMU和差分全球導航衛(wèi)星系統(tǒng)(Global Navigation Satellite Systems,，GNSS)的原點基本重合,，可使用IMU傳感器測量得到的姿態(tài)角計算IMU與地理坐標系之間的轉換矩陣，求解IMU坐標系下標志點的坐標數(shù)據(jù),。

    (3)對激光雷達測量的原始點云數(shù)據(jù)進行預處理,，找到標志點對應的點云坐標。

    (4)對IMU和雷達坐標系下的標志點數(shù)據(jù)進行數(shù)據(jù)擬合,，求得坐標系轉換矩陣,。

    (5)將步驟(2)得到的IMU坐標系下的標志點坐標經過步驟(4)中求解得到的轉換矩陣計算,，轉移到雷達坐標系中，與步驟(3)中得到的測量數(shù)據(jù)進行對比,，進行誤差分析,。

    至此標定方法轉變?yōu)橥ㄟ^數(shù)據(jù)擬合、優(yōu)化的方法求解IMU坐標系與雷達坐標系之間坐標轉換矩陣,。傳統(tǒng)的方法是采用最小二乘法求解,。隨著SLAM技術的發(fā)展，基于3D點云匹配技術的點云拼接方法日趨成熟,。本文借鑒3D點云匹配思路,，將這一標定問題轉換為兩幀點云拼接的問題，進而通過點云匹配方法求解兩個坐標系的坐標轉換矩陣,。常用的3D點云匹配方法有ICP,、NDT等算法，本文選擇ICP算法來求解坐標轉換矩陣,，并與最小二乘法求解結果進行對比,。

2.2 最小二乘法基本原理

    使用最小二乘法進行系統(tǒng)坐標標定，求解的坐標轉換公式如下：

    由此方法能夠得到使三維坐標誤差最小的坐標系轉換矩陣,。

2.3 ICP點云匹配算法原理

    ICP點云匹配算法(迭代最近點算法)是最常用的三維點云匹配算法之一,。ICP算法最早由Besl和Mckay二人提出，主要思想為計算兩個點云中的最近點對進行匹配,，然后根據(jù)配準點對來求得兩個點云之間的坐標轉換矩陣,。ICP算法通常應用于不同時刻兩組點云之間的匹配，從而求得載體的位姿變化,。那么,，可以將在IMU坐標系及雷達坐標系下采集到的標志點點云數(shù)據(jù)作為不同時刻的點云，通過3D點云匹配算法求其位姿變化,，即為兩坐標系的坐標轉換關系,。

    激光雷達探測到的點云包含大量無關點云，需進行預處理來從中提取標志點,。

    預處理分為3個步驟：

    (1)區(qū)域切割,。根據(jù)先驗知識只選定距離在一定范圍之內的點云進行分析。

    (2)地面濾除,。將點云數(shù)據(jù)柵格化,，本文設置柵格大小為0.3×0.3并將每個柵格內的點云按照高度排序，將每個柵格中高度最低的點視為地面點,，將與最低點距離小于閾值的點也當作地面點并一同濾掉,，便于后續(xù)處理。

    (3)標志點提取。地面點云濾除后,，點云信息中只包含標志物,，取最高點當作標志點。

    由上述步驟,，可以得到測量的標志點在雷達坐標系下的坐標,。

    點云預處理標志點提取算法的主要流程如下：

    最終得到的T_3D即轉換矩陣。

3 參數(shù)標定實例及誤差分析

3.1 標定實例

    使用差分GPS測得標志點及車載IMU處的地理位置坐標,，根據(jù)車載IMU給出的姿態(tài)角度,，可以得出車載IMU坐標系下各標志點的三維坐標。

    根據(jù)上述的最小二乘法,，可得到車載慣性坐標系轉換到車載激光雷達坐標系的轉換矩陣,，將計算得出的結果與激光雷達獲得的點云坐標進行比對，其中x,、y,、z的坐標值誤差如表1所示。

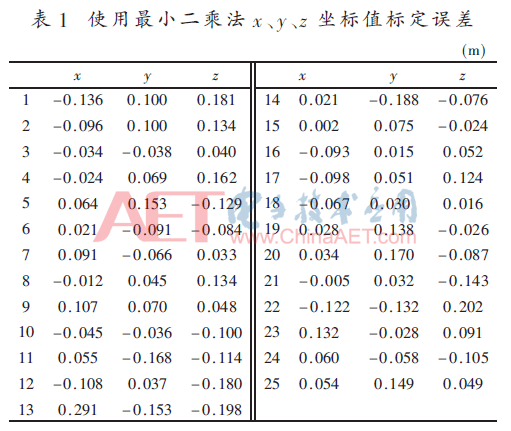
    由上述計算結果可知,，誤差在0.3 m范圍內,，距離誤差的平均值為0.167 m，誤差的標準差為0.068 8 m,。最小二乘法計算結果與實際測量坐標對比如圖4所示,。

    根據(jù)三維點云擬合的ICP算法，得到的x,、y,、z點云坐標與測量坐標的誤差如表2所示。

    由上述計算結果,，誤差在0.4 m范圍內,，距離誤差的平均值為0.197 m，誤差的標準差為0.092 m,，擬合效果較好,。點云匹配方法計算結果與實際測量坐標對比如圖5所示。

3.2 實驗結論

    使用3D點云匹配的方式能夠較好地估算兩個坐標系之間的坐標轉換矩陣,，與最小二乘法標定得出的結果基本一致，說明點云匹配的標定方法是有效的,，這能夠為激光雷達/IMU的參數(shù)聯(lián)合標定提供一種新的思路,。

4 結論

    本文設計利用角反射器作為標志物的車載激光雷達與IMU坐標系的標定方法，通過區(qū)域分割,、地面濾除,、標志點提取的方法提取標志點，借鑒3D點云匹配算法的思路，將激光雷達與IMU坐標系標定問題轉換為點云匹配問題,，通過ICP算法迭代求解兩者之間坐標變換矩陣,，并與最小二乘法結果對比，結果基本一致,，說明基于點云匹配思想的標定方法是有效的,。

參考文獻

[1] KRABILL W B，WRIGHT C W,，SWIFT R N.Airborne laser mapping of assateague national seashore beach[J].Photogrammetic Engineering and Remote Sensing,，2000，66(1)：65-71.

[2] 程金龍,，馮瑩,，曹毓，等.車載激光雷達外參數(shù)的標定方法[J].光電工程,，2013,，40(12)：89-94.

[3] 韓正勇，卜春光,，劉宸.一種針孔相機與三維激光雷達外參標定方法[J].傳感器與微系統(tǒng),，2018，37(4)：9-12,，16.

[4] 韓棟斌,，徐友春，王任棟,，等.基于多對點云匹配的三維激光雷達外參數(shù)標定[J].激光與光電子學進展,，2018，55(2)：455-462.

[5] 熊爍,，葉伯生,，蔣明.機器人工具坐標系標定算法研究[J].機械與電子，2012(6)：60-63.

[6] 余和青,，劉文波,，鄧釗波，等.最小二乘法視覺系統(tǒng)標定研究[J].日用電器,，2014(12)：61-64.

[7] 段建民,，王昶人，任璐,，等.基于多層激光雷達的可行駛區(qū)域信息提取算法[J].電子技術應用,，2017，43(10)：78-82.

[8] 王建中,，楊璐.基于GPS定向測姿系統(tǒng)的研究[J].電子技術應用,，2016,，42(9)：14-18.

[9] 蔣從元，楊杰.基于分布式多跳誤差估計目標位置感知算法[J].電子技術應用,，2017,，43(11)：95-98.

[10] 趙立峰.整體最小二乘法及其在坐標轉換中的應用[J].林業(yè)科技情報，2011,，43(4)：114-115.

[11] 楊仕平,，范東明，龍玉春.基于整體最小二乘法的任意旋轉角度三維坐標轉換[J].大地測量與地球動力學,，2013,，33(2)：114-119.

[12] 韓明瑞.基于激光LiDAR的室外移動機器人三維定位與建圖[D].南京：東南大學，2016.

[13] ZHANG Z.Iterative point matching for registration of free-form curves and surfaces[J].International Journal of Computer Vision,，1994,，13(2)：119-152.

[14] MINGUEZ J，MONTESANO L,，LAMIRAUX F.Metric-based iterative closest point scan matching for sensor displacement estimation[J].IEEE Transactions on Robotics,，2006，22(5)：1048-1054.

[15] BIBER P,，STRASSER W. The normal distributions transform：a new approach to laser scan matching[C].Proceedings of 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems,，2003(IROS 2003)，2003,，3：2743-2748.

[16] 沈海平,，達飛鵬，雷家勇.基于最小二乘法的點云數(shù)據(jù)拼接研究[J].中國圖象圖形學報,，2005(9)：1112-1116.

[17] 鄭忠陽.基于車載激光雷達的點云配準算法及應用技術研究[D].長沙：國防科學技術大學,，2015.

作者信息:

吳昱晗，王蘊寶,，薛慶全,，郄曉斌，李志強

(北京航天發(fā)射技術研究所,，北京100076)