摘 要: 比特置換" title="比特置換">比特置換操作在對(duì)稱密碼算法" title="密碼算法">密碼算法中使用頻率非常高,它所采用的非線性變換能夠?qū)崿F(xiàn)高安全性。但現(xiàn)有的可編程處理器對(duì)單個(gè)比特的操作并不直接支持。就此問題,研究了比特置換操作在處理器上的高效靈活實(shí)現(xiàn)方法,提出了一種基于Benes網(wǎng)絡(luò)結(jié)構(gòu)" title="網(wǎng)絡(luò)結(jié)構(gòu)">網(wǎng)絡(luò)結(jié)構(gòu)的硬件可實(shí)現(xiàn)的比特置換結(jié)構(gòu)及其在不同指令集上的應(yīng)用,并在FPGA上進(jìn)行了驗(yàn)證。
關(guān)鍵詞: 比特置換 專用指令集微處理器 查找表" title="查找表">查找表 Benes網(wǎng)絡(luò)結(jié)構(gòu)
目前,通用微處理器大多是以字為單位進(jìn)行操作的,它的指令結(jié)構(gòu)ISA(Instruction-set Architecture)不支持小于一個(gè)字的數(shù)據(jù)操作。而單比特的置換操作在分組密碼算法中使用頻率非常高,是提高算法安全性的重要手段;而且比特置換操作在處理器中快速高效的特點(diǎn),也將影響密碼處理的整體性能。但在現(xiàn)有的指令結(jié)構(gòu)處理器中,任意的比特置換通常都采用邏輯操作或查找表的方式實(shí)現(xiàn)[1],即使一個(gè)簡單的置換操作(如循環(huán)移位),也需要多條指令才能完成。根據(jù)相關(guān)研究可知,一個(gè)n比特的置換操作,它的指令級(jí)復(fù)雜度是O(n),處理速度也將隨著n的增大而不斷降低。對(duì)于目前實(shí)時(shí)的網(wǎng)絡(luò)通信來說,這顯然是不可容忍的。因此,針對(duì)這一問題在一些專用指令集微處理器ASIP(Application-Specific Instruction-Set Processor)中,增加了特殊的置換指令,如多媒體處理器PLX中增加了MIX、MUX和Perm等指令[2],但這些指令并不能滿足n-bit數(shù)據(jù)的任意置換操作。本文提出了一種在處理器中實(shí)現(xiàn)比特置換的方法,給出了相應(yīng)的比特置換指令及其操作結(jié)構(gòu)。
1 密碼學(xué)中的比特置換及其一般實(shí)現(xiàn)方式
1.1 密碼學(xué)中的比特置換
比較置換操作能使輸入數(shù)據(jù)中第i比特置換到輸出數(shù)據(jù)的第j比特上,而且置換過程中各位源數(shù)據(jù)之間不發(fā)生計(jì)算關(guān)系。輸入的n比特?cái)?shù)據(jù)需要log2n比特位置信息或配置信息。
置換是密碼算法中隱藏明文信息中冗余度的重要手段,通過位置置換可以實(shí)現(xiàn)明文到密文的擴(kuò)散。置換按明密文映射關(guān)系分為三類:直接置換、擴(kuò)展置換和壓縮置換。直接置換指明密文間是一一映射關(guān)系,且明文的每一位都有到密文的映射;擴(kuò)展置換指明密文間為一對(duì)多的映射關(guān)系,它使得密文對(duì)明文的依賴性傳播得更快;壓縮置換指明密文間是一一映射關(guān)系,但并不是明文的每一位都有到密文的映射。置換輸入和輸出位寬根據(jù)算法和置換類型的不同而有所不同。例如DES算法中有64-bit初始置換IP、末尾置換IP-1以及輪運(yùn)算中的32-bit P置換[3]。
1.2 邏輯操作方式
邏輯操作方式是指采用AND、OR、SHIFT等簡單邏輯操作實(shí)現(xiàn)復(fù)雜的比特置換操作。在此方式下,每對(duì)1 bit進(jìn)行置換,處理器需要進(jìn)行四步操作:①產(chǎn)生目標(biāo)比特的MASK參數(shù);②提取相應(yīng)比特值(AND指令);③將該比特移至相應(yīng)位置(SHIFT指令);④存儲(chǔ)到相應(yīng)寄存器中(OR指令)。由上述過程可知,一個(gè)n-bit的置換操作需要4n條指令才能完成。盡管一些處理器中針對(duì)這一問題有所改進(jìn),將1 bit置換操作的指令壓縮到2條——汲取指令(EXTRACT)和放置指令(DEPOSIT),但n-bit置換操作仍需要2n條指令,處理性能沒有明顯提高。
1.3 查找表方式
查找表方式是另一種實(shí)現(xiàn)比特置換的方法,它在速度上與邏輯操作相比有所提高,但需要大量的存儲(chǔ)空間放置控制信息。完成一個(gè)n-bit的置換操作需要m個(gè)查找表,每個(gè)表的容量為2n/m×nbit。以64-bit輸入數(shù)據(jù)為例,當(dāng)m=1時(shí),完成一次任意置換需要一個(gè)264×64bit的查找表,這在現(xiàn)有微處理器結(jié)構(gòu)中是無法實(shí)現(xiàn)的;當(dāng)m=8時(shí),完成一次任意置換需要8個(gè)容量為28×64bit的查找表。每個(gè)表代表源操作數(shù)中連續(xù)8-bit的置換,表中除了8-bit置換的目標(biāo)位置外,其他位置均為0,此時(shí)共需要23條指令來完成64-bit置換:8條Extract指令獲得表的索引值、8條Load指令置換相應(yīng)比特、7條OR指令鏈接8個(gè)8-bit置換后的數(shù)據(jù)。這種方法相對(duì)于邏輯操作方式來說指令條數(shù)減少了很多,但它在實(shí)際執(zhí)行中,Load指令往往遇到未命中Cache的情況,所以實(shí)現(xiàn)n-bit的置換操作需要的復(fù)雜度一般為O(n)。
2 比特置換操作的優(yōu)化實(shí)現(xiàn)
2.1 Butterfly結(jié)構(gòu)
目前,Butterfly結(jié)構(gòu)[4]及其他一些相似的結(jié)構(gòu)都廣泛應(yīng)用于信息處理領(lǐng)域中,如數(shù)字信號(hào)處理中的快速傅里葉變換(FFT)等。圖1(a)中給出了8-bit輸入的Butterfly結(jié)構(gòu),圖1(b)中給出了相應(yīng)的Inverse Butterfly結(jié)構(gòu)。
2.2 Benes網(wǎng)絡(luò)結(jié)構(gòu)
Benes網(wǎng)絡(luò)結(jié)構(gòu)由一個(gè)Butterfly結(jié)構(gòu)鏈接一個(gè)Inverse Butterfly結(jié)構(gòu)組成,它是一種可重排網(wǎng)絡(luò),能實(shí)現(xiàn)輸入端到輸出端的所有置換。完成n-bit置換操作需log2n級(jí)Butterfly變換和log2n級(jí)Inverse Butterfly變換。對(duì)于一個(gè)64-bit置換,則需要2log2n=12級(jí)變換,且每一級(jí)需要n/2-bit配置信息。在處理器中執(zhí)行置換操作需要一條Butterfly指令和一條Inverse Butterfly指令及l(fā)og2n個(gè)n-bit配置信息。
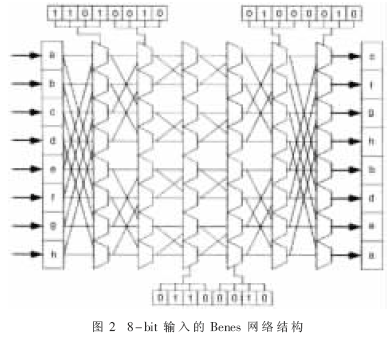
圖2給出了一個(gè)8-bit輸入的Benes網(wǎng)絡(luò)結(jié)構(gòu),能完成(abcdefgh)到(cfghbdea)的置換。根據(jù)配置信息,它的置換過程如下:Butterfly指令完成(abcdefgh)->(abgdefch)->(gdabehcf)->(dgabehfc);Inverse Butterfly指令完成(dgabehfc)->(gcbaehcf)->(bdgacfeh)->(cfghbdea)。
2.3 比特置換指令
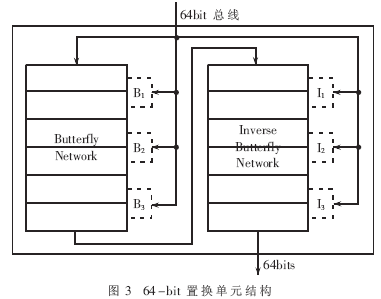
比特置換單元內(nèi)部設(shè)置了一定的緩存區(qū),用于存儲(chǔ)配置信息,如圖3所示的B1、B2、B3和I1、I2、I3。由于不同ASIP中指令格式存在差異,這些內(nèi)部緩存區(qū)是可選擇的。由于Inverse Butterfly指令類似于Butterfly指令,下面以Butterfly指令為例進(jìn)行說明。對(duì)于超長指令字格式(VLIW),支持多操作數(shù)方式,不需要內(nèi)部寄存器存儲(chǔ)配置信息,其指令可描述為:Butterfly Rd,Rs,B1,B2,B3。其中Rd為置換數(shù)據(jù)目的地址,Rs為置換數(shù)據(jù)源地址,B1、B2、B3為配置信息的外部存儲(chǔ)地址,即一條Butterfly指令包括Rs、B1、B2、B3四個(gè)源操作數(shù)。對(duì)于精簡指令格式(RISC),最多支持兩個(gè)源操作,相應(yīng)指令可描述為:Butterfly Rd,Rs,B3。即需要將配置信息B1、B2、I1、I2在進(jìn)行置換操作前裝入到置換單元內(nèi)部緩存區(qū)中,而B3、I3則從外部存儲(chǔ)器中獲得。對(duì)于超標(biāo)量結(jié)構(gòu)處理器,假設(shè)其有兩路并行處理通路,則Butterfly指令與Inverse Butterfly指令可并行執(zhí)行。對(duì)于所采用的不同指令格式,具體操作指令數(shù)也不同。
3 性能比較
如果一個(gè)處理器可以支持比特置換操作,則其比特置換操作的延時(shí)必須與邏輯運(yùn)算單元(ALU)的時(shí)鐘頻率相匹配。在ALU中主要是乘法器[5]延時(shí)較大,通常占用3~5個(gè)時(shí)鐘周期" title="時(shí)鐘周期">時(shí)鐘周期,因此只有使比特置換操作延時(shí)小于乘法運(yùn)算延時(shí),才能在不影響處理器整體性能的前提下,使處理器支持比特置換操作。而邏輯操作方式與查找表方式的比特置換實(shí)現(xiàn)方法所占用的時(shí)鐘周期都遠(yuǎn)遠(yuǎn)大于3個(gè)時(shí)鐘周期,如表1所示。當(dāng)采用Benes網(wǎng)絡(luò)結(jié)構(gòu)時(shí),僅執(zhí)行兩次Butterfly指令,在性能上得到了很大提高,使n-bit 的比特置換操作的復(fù)雜度從O(n)降至O(log(n))。
比特置換是現(xiàn)代對(duì)稱密碼算法中的一個(gè)基本操作,但由于它比其他操作延時(shí)大且需要大量的控制信息,使得目前的通用處理器并不支持比特置換操作。本文針對(duì)上述兩個(gè)問題提出的解決方案,使其可以在處理器中快速實(shí)現(xiàn),并以64-bit置換為例,在FPGA上對(duì)這一結(jié)構(gòu)進(jìn)行了驗(yàn)證,結(jié)果僅占用700個(gè)邏輯單元,最高時(shí)鐘頻率達(dá)到了220MHz。采用ASIC實(shí)現(xiàn)時(shí),其性能還將在此基礎(chǔ)上顯著提高,從而滿足網(wǎng)絡(luò)通信等方面的需求。
參考文獻(xiàn)
1 R B Lee,Z Shi,X Yang.Efficient permutation instructions for fast software cryptography[J].IEEE Micro,2001;21(6):56~69
2 Ruby B Lee,A Murat Fiskiran.PLX:A fully subword parallel instruction set architecture for fast scalable multimedia pro-cessing.Supported in part by HP,NSF and Kodak:2~3
3 Bruce Schneier著,吳世忠,祝世雄,張文政譯.應(yīng)用密碼學(xué)[M].北京:機(jī)械工業(yè)出版社,2000:225~233
4 Xiao Yang,Manish Vachharajani,Ruby B Lee.Fast Subword Permutation Instruction Based on Butterfly Networks[J].In:Proceedings of SPIE,Media Processor 2000,January 2000:80~86
5 Zhijie Shi,Xiao Yang,Ruby B Lee.Arbitrary Bit Permuta-tions in One or Two Cycles[J].In:Proceedings of the IEEE 14th International Conference on Application-Specific Systems,Architectures and Processors,June 2003