設(shè)計(jì)快速乘法器,，通常要重點(diǎn)處理三個(gè)關(guān)鍵問(wèn)題：減少部分積產(chǎn)生、加速部分積累加和提高最終多位數(shù)相加速度,。例如,，用傳統(tǒng)的乘法運(yùn)算模式處理16位×16位所用的時(shí)間為t_總=t_{產(chǎn)生16行部分積}+_{t16行部分積累加成最終積}。若運(yùn)用改進(jìn)波茲(Booth)算法以后,，可以減少部分積的產(chǎn)生,。而基于改進(jìn)波茲算法的乘法器設(shè)計(jì),，在后續(xù)部分積相加的過(guò)程中，無(wú)論采用哪種處理方式,，如華萊氏樹(shù)結(jié)構(gòu)等,，都不可避免地要解決符號(hào)位擴(kuò)展陣列問(wèn)題。本文提出了一種新的基于改進(jìn)波茲算法的邏輯設(shè)計(jì)" title="邏輯設(shè)計(jì)">邏輯設(shè)計(jì)來(lái)處理符號(hào)位部分：通過(guò)簡(jiǎn)單地運(yùn)用‘或門’,、‘異或門’來(lái)優(yōu)化乘法器的局部速度和面積兩方面的性能,。
1 改進(jìn)波茲算法
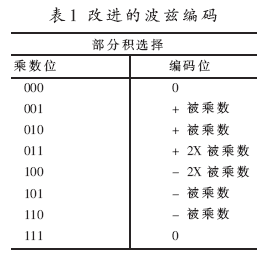
　　改進(jìn)波茲算法MBA(Modified Booth′s Algorithm)^[1]是建立在波茲算法^[2]基礎(chǔ)上的。對(duì)乘數(shù)三位一組的劃分包含了一個(gè)重疊位,，每一組的三位按表1編碼,，并形成一個(gè)部分積。由此而產(chǎn)生5個(gè)系數(shù)：±1,、±2,、0。在部分積的累加過(guò)程中,，減法也就是補(bǔ)碼相加,。經(jīng)過(guò)編碼以后，通過(guò)高低電平信號(hào)對(duì)符號(hào)位進(jìn)行指示,。n位乘數(shù)乘以m位被乘數(shù)會(huì)產(chǎn)生n+m位積,。因此累加過(guò)程中由于對(duì)負(fù)數(shù)補(bǔ)碼的相加，每個(gè)部分積必須把符號(hào)位擴(kuò)展到最高位(第n+m-1位),，以此來(lái)保證后續(xù)運(yùn)算的正確性,。若以8位X×8位Y為例，產(chǎn)生的部分積陣列如圖1所示,。由于部分積含有±2X,，因此其字長(zhǎng)為9位，即A0～A8,，第10位A9為符號(hào)位,。在做減法補(bǔ)碼運(yùn)算時(shí)，其符號(hào)位應(yīng)擴(kuò)充至最高位(第15位),，再加上相應(yīng)每組最高位,，即y1。B,、C、D,、E也按此規(guī)律產(chǎn)生,。8位×8位最終產(chǎn)生16位積。

?

　　觀察圖1可以發(fā)現(xiàn)在部分積陣列中,，有相當(dāng)大的一部分是符號(hào)位擴(kuò)展陣列,，并且隨著兩個(gè)相乘數(shù)的位數(shù)成倍地增加,，符號(hào)位擴(kuò)展陣列也不斷擴(kuò)大，因此考慮對(duì)這個(gè)特殊陣列的處理就相當(dāng)有價(jià)值,。
2 ‘或’-‘異或’快速算法處理符號(hào)位部分
　　對(duì)符號(hào)位擴(kuò)展陣列單獨(dú)處理,，邏輯設(shè)計(jì)則按照下面順序來(lái)進(jìn)行：
　　(1)若乘數(shù)有偶數(shù)個(gè)位即2k(k=1,2……n)，那么就會(huì)產(chǎn)生k+1行部分積,。在部分積中,，有k行符號(hào)擴(kuò)展位，符號(hào)擴(kuò)展位陣列的最大寬度為2k-1個(gè)位,；若乘數(shù)有奇數(shù)個(gè)位,，即2k+1(k=0,1,2......n)，那么就會(huì)產(chǎn)生k+1行部分積,。在部分積中,，有k行符號(hào)擴(kuò)展位，符號(hào)擴(kuò)展位陣列的最大寬度為2k個(gè)位,。
　　(2) 若編碼結(jié)果為負(fù)數(shù),，那么產(chǎn)生該行的所有符號(hào)位都是1，否則都為0,。
　　(3) 除了第0列,，對(duì)符號(hào)位擴(kuò)展陣列每一列進(jìn)行奇偶劃分，即第1,、3,、5……為奇數(shù)列，第2,、4,、6……為偶數(shù)列。
　　(4) 符號(hào)位擴(kuò)展陣列和的偶數(shù)位與該列上(從上至下)最后一位相關(guān)聯(lián),。該陣列和的奇數(shù)位等于該列上所涉及位的‘或’運(yùn)算,，偶數(shù)位等于與該位相關(guān)聯(lián)的那位與低一位的奇數(shù)列的和位的‘異或’運(yùn)算，第0位等于第0行的編碼產(chǎn)生的符號(hào)信號(hào),。
　　以8位×8位的例子來(lái)說(shuō)明：r0~r6是符號(hào)位陣列累加的和位,，s0~s3表示陣列第0行到第3行，如圖2所示,。

　　當(dāng)乘數(shù)有奇數(shù)個(gè)位時(shí),，符號(hào)位擴(kuò)展陣列排布如圖4所示。

　　求證方法類似于偶數(shù)位乘數(shù),，得到的結(jié)論為：
　　r_2i-1=sign[i-1]|…|sign^[1]|sign[0],r_2i-2=sign[i-1]^r_2i-3,。
4 算法實(shí)現(xiàn)
　　實(shí)現(xiàn)這一設(shè)計(jì)很容易：根據(jù)設(shè)計(jì)規(guī)則，r₃,、r₅……r_2i-1
　　位全部由‘或門’來(lái)實(shí)現(xiàn),，r₂,、r₄、r₆……r_2i-2位全部由‘異或門’來(lái)實(shí)現(xiàn),，r₀,、r₁用編碼產(chǎn)生的符號(hào)指示信號(hào)表示。把8位×8位的例子用‘或門’和‘異或門’實(shí)現(xiàn)如圖5所示,，圖中用了2個(gè)‘或門’和3個(gè)‘異或門’,。

5 性能評(píng)估
　　該設(shè)計(jì)方案的性能評(píng)價(jià)從如下兩方面考慮：
　　(1)從速度和面積兩方面性能考慮，符號(hào)位擴(kuò)展陣列作為一個(gè)模塊單獨(dú)設(shè)計(jì),。
　　首先,，把原本符號(hào)位之間的累加轉(zhuǎn)換成用‘或’-‘異或’進(jìn)行處理，既大大降低了門的使用數(shù)量,，從而減小了該硬件乘法器模塊所占的面積,，也避免了累加過(guò)程中的進(jìn)位等待問(wèn)題而提高了速度。如果不對(duì)符號(hào)位擴(kuò)展陣列單獨(dú)處理,，而是在后續(xù)處理的過(guò)程中選擇特殊壓縮器來(lái)進(jìn)一步解決累加的速度問(wèn)題,，其面積上的增加是顯而易見(jiàn)的。
　　(2)考慮該設(shè)計(jì)結(jié)果對(duì)后續(xù)部分積處理的影響,。
　　因?yàn)橥ㄟ^(guò)符號(hào)位擴(kuò)展陣列的特性可以知道,，和的位數(shù)就是以第0行部分積中的符號(hào)擴(kuò)展位的位數(shù)，不產(chǎn)生多余的累加行,。因此陣列最終產(chǎn)生一行和位,，與現(xiàn)在所知的其他處理方法相比，沒(méi)有多余的位與除去符號(hào)位擴(kuò)展陣列的部分積進(jìn)行相加,。并且該行和位也不作為額外的累加行介入部分積累加,。在相關(guān)文獻(xiàn)中，對(duì)符號(hào)位擴(kuò)展陣列處理有使用預(yù)求和并加上修正位的方法：先假設(shè)所有n位×n位符號(hào)位擴(kuò)展陣列中每個(gè)位都是1,，預(yù)算出最后的和,，然后根據(jù)符號(hào)指示信號(hào)對(duì)相應(yīng)行加1，并將這個(gè)1作為符號(hào)修正位^[3],。也有根據(jù)等式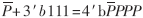,，對(duì)符號(hào)擴(kuò)展部分做相應(yīng)恒等變形處理的方法^[4]。這些方法除了產(chǎn)生與符號(hào)位擴(kuò)展陣列寬度相同的一行位以外,，還有額外的位要累加到部分積上,。以8位×8位乘法用三種" title="三種">三種不同方案處理符號(hào)位部分所得部分積如圖6所示。圖中r₀~r₆作為符號(hào)位陣列累加的和位,，作為符號(hào)修正位,。

?