??? 摘 要： 提出了一種可以應(yīng)用于CDMA系統(tǒng)的多步長(zhǎng)功率控制算法" title="控制算法">控制算法,，本算法根據(jù)接收端的實(shí)測(cè)信干比" title="信干比">信干比與目標(biāo)信干比的差值,，從4個(gè)步長(zhǎng)中選取一個(gè)，對(duì)發(fā)射端的發(fā)射功率" title="發(fā)射功率">發(fā)射功率進(jìn)行調(diào)整,。由于步長(zhǎng)是有限個(gè)固定值，因此該算法易于實(shí)現(xiàn)。通過(guò)仿真證明,，該算法性能優(yōu)于可實(shí)際應(yīng)用的FS算法,，接近于性能理想而難于實(shí)現(xiàn)的FMA算法。
??? 關(guān)鍵詞： 功率控制? 多步長(zhǎng)? FS算法? FMA算法? 信干比
?
??? CDMA系統(tǒng)是一種自干擾系統(tǒng),，其容量受限于系統(tǒng)的干擾水平,。在CDMA系統(tǒng)中，必須在滿(mǎn)足傳輸業(yè)務(wù)要求的信干比(SIR)條件下,，盡量降低發(fā)射端的發(fā)射功率,。因此在CDMA系統(tǒng)中功率控制技術(shù)具有非常重要的作用。有效的功率控制技術(shù)可以很好地控制遠(yuǎn)近效應(yīng)和多址干擾,，從而提高系統(tǒng)容量,。在現(xiàn)有的功率控制算法中，F(xiàn)oschini和Miljanic提出的FMA算法[5]是一種具有理想性能的經(jīng)典算法,。在FMA算法中,，每次迭代后發(fā)射功率的改變幅度可以選取需要的任意值,而在實(shí)際系統(tǒng)中這是在一定技術(shù)條件和成本條件下難以實(shí)現(xiàn)的，因此FMA算法的意義僅僅停留在理論研究上,。Kim在文獻(xiàn)[7]中提出的定步長(zhǎng)（FS）算法則是在每次功率更新中對(duì)接收SIR進(jìn)行判決以確定對(duì)發(fā)射功率進(jìn)行增加或減少,其步長(zhǎng)固定,，通常為1dB或0.5dB。FS算法在實(shí)際應(yīng)用方面具有明顯的優(yōu)勢(shì),，在第二代IS－95系統(tǒng)和第三代WCDMA系統(tǒng)中都采用了該算法,。但由于FS算法在每次迭代中對(duì)發(fā)射功率的改變幅度是固定的，其收斂速度和收斂精度無(wú)法兼顧,，因此該算法性能不夠理想,。
??? 針對(duì)FMA和FS算法的不足，本文提出了一種可以應(yīng)用于實(shí)際系統(tǒng)的多步長(zhǎng)（MS）功率控制算法,，采用4個(gè)確定步長(zhǎng),，在每次迭代中根據(jù)需要選取一個(gè)對(duì)發(fā)射功率進(jìn)行調(diào)整。顯然這是一種可以實(shí)際應(yīng)用的算法,。由于有大小不等的多個(gè)步長(zhǎng),，因此在對(duì)發(fā)射功率進(jìn)行調(diào)整的過(guò)程中可以獲得較高的收斂速度和精度，其性能應(yīng)優(yōu)于FS算法,。本文對(duì)MS算法和FS算法以及FMA算法進(jìn)行了仿真,，結(jié)果顯示，本算法在性能上遠(yuǎn)遠(yuǎn)優(yōu)于FS算法,，與FMA算法的性能比較接近,。
1 系統(tǒng)模型
??? 假設(shè)一個(gè)蜂窩小區(qū)中有N個(gè)移動(dòng)臺(tái)" title="移動(dòng)臺(tái)">移動(dòng)臺(tái)共用一個(gè)信道，并且假設(shè)移動(dòng)臺(tái)i屬于第i個(gè)基站,。本文中只考慮上行鏈路" title="鏈路">鏈路的情況,。γi表示第i個(gè)基站接收到第i個(gè)移動(dòng)臺(tái)信號(hào)的CIR,，當(dāng)γi大于等于給定的目標(biāo)信干比γtgt時(shí)，可以認(rèn)為基站能夠正確接收該移動(dòng)臺(tái)的信號(hào),。γi可以用下式表示：
??? 
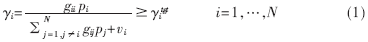
其中pi表示移動(dòng)臺(tái)i的發(fā)送功率；gij表示移動(dòng)臺(tái)j到基站i的路徑增益,，該路徑增益由路徑衰落,、陰影衰落和多徑衰落共同組成；vi是基站i處的背景噪聲,。所有的gij組成的矩陣稱(chēng)為鏈路增益矩陣,，記為G。將G中元素歸一化得到矩陣H,H中的元素hij=γitgtgij/gii,，hii=0,，ηi=γitgtvi/gii。若考慮時(shí)變信道,，則H矩陣中的元素值隨時(shí)間的改變而改變,，可用下式表示：
??? 
其中Hav表示H矩陣的均值，是一個(gè)確定值,，而ΔH(k)在每次迭代中是一個(gè)按某個(gè)分布隨機(jī)產(chǎn)生的不確定值,。（2）式用元素形式表示如下：
??? 
其中p為發(fā)送功率矢量，Ha v為歸一化的鏈路增益的均值矩陣,，η為噪聲矢量,。本文中功率控制問(wèn)題主要涉及通過(guò)測(cè)量γi的值并結(jié)合γtgt來(lái)確定發(fā)送功率矢量p，使得矢量p收斂于最佳發(fā)送功率矢量popt,，即：
??? 
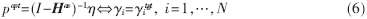
??? 由于實(shí)際系統(tǒng)中移動(dòng)臺(tái)有最大發(fā)射功率限制,，用下式對(duì)發(fā)射功率進(jìn)行限制：
??? 
其中pmax為移動(dòng)臺(tái)最大發(fā)射功率。假設(shè)（5）式在（7）式的范圍內(nèi)有解并且矩陣H(k)的譜半徑小于1,，則稱(chēng)系統(tǒng)是可行的,。H矩陣的譜半徑為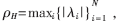
其中λi是H矩陣的特征值。
2 功率控制算法
??? 將新功率控制算法表示如下：
??? 
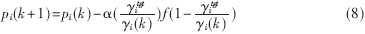
其中pi(k)是第i個(gè)移動(dòng)臺(tái)的發(fā)射功率,，γi(k)是基站在第k次迭代中接收到第i個(gè)移動(dòng)臺(tái)信號(hào)的CIR,，f(·)是一個(gè)有上下邊界的奇函數(shù)，本文采用sign(·),；α(·)是一個(gè)分段函數(shù),，表示每次迭代對(duì)功率值的改變幅度。在本文中不考慮時(shí)延的影響,。由（8）式可知本功率控制算法是一個(gè)一階完全分布式功率控制算法,。如果取常數(shù)1并且取恒等函數(shù)，則本算法退化為文獻(xiàn)[5]中的FMA算法,；若取常數(shù)1且f(·)取符號(hào)函數(shù),，則算法退化為文獻(xiàn)[7]中的FS算法,；而在文獻(xiàn)[8]中考慮了當(dāng)α(·)取常數(shù)1時(sh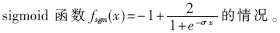í)采用
??? 考慮到實(shí)際系統(tǒng)有最大發(fā)射功率限制，將(8)式表示如下:
??? 
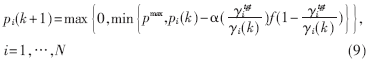
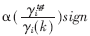
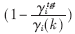其中pmax是最大發(fā)射功率,。在本算法中假設(shè)接收端可以得到γitgt和γi的值,，（在上行鏈路中接收端是基站），而發(fā)送端可以得到pi(k)的值,。接收端通過(guò)對(duì)
進(jìn)行計(jì)算,，獲得功率控制指令，然后將其反饋到發(fā)送端以更新發(fā)射功率,。
??? 定義：對(duì)于H矩陣,，如果滿(mǎn)足
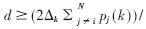
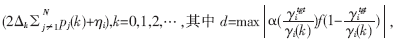則對(duì)γi的任意初始值γi(k=0)，γi(k)都將收斂于
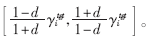證明參見(jiàn)文獻(xiàn)[8],。
3 仿真分析
??? 在本文的仿真中考慮8個(gè)移動(dòng)臺(tái)共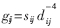用一個(gè)信道的情況,。用
表示平均鏈路增益，其中sij為陰影衰落因子,，
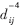表示自由空間衰落,，dij為基站i和移動(dòng)臺(tái)j之間的距離。仿真中小區(qū)半徑設(shè)為1 000米,，每個(gè)移動(dòng)臺(tái)與基站的距離在0～1 000米隨機(jī)產(chǎn)生,，每個(gè)移動(dòng)臺(tái)初始發(fā)射功率在0～1W隨機(jī)產(chǎn)生，最大發(fā)射功率p_max=1.995 3W,。陰影衰落服從對(duì)數(shù)正態(tài)分布,，即sij=10ζ/10，其中ζ是均值為0標(biāo)準(zhǔn)方差為8dB的高斯隨機(jī)變量,。目標(biāo)信干比采用
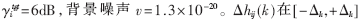范圍內(nèi)按照均勻分布隨機(jī)取值,。未擴(kuò)頻信號(hào)速率R=8kbps，擴(kuò)頻碼片速率w＝1.28Mcps,，對(duì)FMA,、FS算法以及本文提出的MS算法進(jìn)行仿真。將FS,、FMA,、MS分別用dB形式表示如下：
??? 
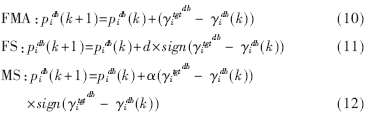
其中(11)式中的d取1，(12)式中的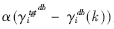
為一分段函數(shù),，用于確定每次迭代的步長(zhǎng),，表示如下：
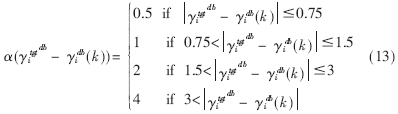
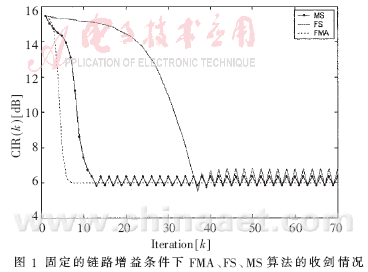
??? 首先在固定的鏈路增益（Δk=0）條件下分別運(yùn)用三種算法進(jìn)行仿真。仿真結(jié)果用圖1表示,。
?
?
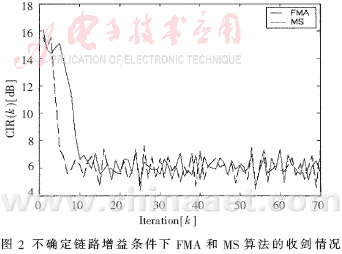
??? 由圖1可以看出,，與FS算法相比，MS算法具有更快的收斂速度和更好的收斂精度,，其性能比較接近FMA算法,。然后在不確定鏈路增益（Δk=0.2）條件下的分別運(yùn)用以上三種算法進(jìn)行迭代運(yùn)算,。仿真結(jié)果如圖2和圖3所示。其中圖2顯示了FMA和MS算法的結(jié)果,，圖3則是FS和MS的仿真結(jié)果,。圖2證明在時(shí)變信道中MS算法可以獲得接近FMA算法的性能；而由圖3可以看到,，MS算法的性能明顯優(yōu)于FS算法,。
?
?
?
??? 定義代價(jià)函數(shù)如下式：
??? 
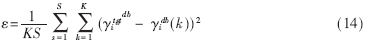
其中K表示調(diào)用功率控制算法的次數(shù)，S表示每次調(diào)用功率控制算法過(guò)程中進(jìn)行迭代的次數(shù),。
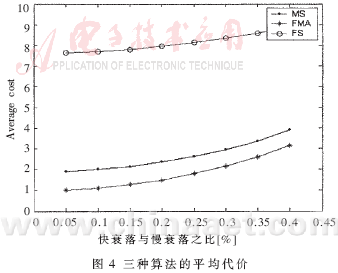
??? 代價(jià)函數(shù)實(shí)質(zhì)上反映的是功率控制算法的收斂速度與精度的綜合指標(biāo)，通過(guò)代價(jià)函數(shù)計(jì)算得到的數(shù)據(jù)越小,，算法的性能越好,。仿真中S＝300，K＝1 000,。仿真結(jié)果如圖4所示,。圖4中的橫坐標(biāo)表示快衰落的最大值與慢衰落之比。通過(guò)圖4可以得到這樣的結(jié)論,，最大快衰落與慢衰落之比在0.05～0.4的條件下,，MS算法的代價(jià)都遠(yuǎn)遠(yuǎn)小于FS算法，略大于FMA,。
?
?
??? 本文提出了一種多步長(zhǎng)的功率控制算法,，該算法是一種可以實(shí)際應(yīng)用的算法。通過(guò)在慢衰落和快衰落環(huán)境中的仿真研究,，證明該算法比FS算法具有更快的收斂速度和收斂精度,，與理想的FMA算法比較接近。
參考文獻(xiàn)
[1] AEIN J M. Power balancing in systems employing frequency reuse. COMSAT Tech.Rev., 1973,3(2).
[2] ?MEYERHOFF H J.Method for computing the optimum power balance in multibeam satellite. COMSAT Tech.Rev.,1996,4(7):772-775.
[3] ?ZANDER J. Performance of optimum transmitter power control in cellular radio systems. IEEE Trans.Veh,Technol.1992,41(1):57-62.
[4] ?ZANDER J. Distributed cochannel interference control in cellular radio systems. IEEE Trans.Veh,Technol.1992,41(3):305-311.
[5] ?FOSCHINI G J, MILJANIC Z. A simple distributed autonomous power control algorithm and its convergence.IEEE Trans, Veh, Technol.,1993,42(4):466-468.
[6]?GRANDHI S A, ZANDER J, YATES R D. Constrained power control.Wireless Personal Commun.,1995,(4):257-270.
[7] ?KIM D. On the convergence of the fixed-step power control algorithms with binarv feedback for mobile communication systems.IEEE Trans.Commun.,2001,49(2):249-252.
[8] ?UYKAN Z, HEIKKI? N. Proportional power control algorithm for time varying link gains in cellular systems.IEEE Trans.Veh,Technol., 2006,55(1).