0 引言
在電子對(duì)抗領(lǐng)域中輻射源測(cè)向是一個(gè)基本問(wèn)題,。而干涉儀測(cè)向系統(tǒng)是目前精度相對(duì)較高的一種測(cè)向體制因而被廣泛使用,。干涉儀測(cè)向體制的主要優(yōu)點(diǎn)是精度高和工作頻率范圍寬,，但目前使用的干涉儀系統(tǒng)還存在不足,，主要包括：(1)在被動(dòng)制導(dǎo)等領(lǐng)域中測(cè)向精度仍然不夠：(2)對(duì)現(xiàn)代雷達(dá)使用的寬帶脈壓信號(hào)適應(yīng)能力有限；(3)有待進(jìn)一步提高系統(tǒng)的工作頻率范圍,。針對(duì)上述問(wèn)題,，本系列論文提出了數(shù)字化寬帶測(cè)向系統(tǒng)的整體解決方案，重點(diǎn)討論數(shù)字化相位差測(cè)量及誤差分析、概率解模糊算法和在測(cè)向精度和工作頻率范圍約束下如何進(jìn)行天線陣列基線設(shè)計(jì)三個(gè)問(wèn)題,。
本文是系列論文的第一篇,，給出了數(shù)字化寬帶測(cè)向系統(tǒng)模型，討論了數(shù)字化相位差測(cè)量方法,，推導(dǎo)了數(shù)字化相位測(cè)量的數(shù)字化方法誤差函數(shù)和由通道噪聲引起的信號(hào)相位誤差分布密度函數(shù),。相位差測(cè)量的精度直接影響系統(tǒng)測(cè)向的精度，還會(huì)影響解相位差模糊和天線陣列基線設(shè)置等一系列系統(tǒng)設(shè)計(jì)問(wèn)題,。傳統(tǒng)的相位差測(cè)量方法都是利用窄帶信號(hào)干涉原理把相位差轉(zhuǎn)化為幅度進(jìn)行測(cè)量的,，因而其只能夠適用于窄帶信號(hào)的相位差測(cè)量，且測(cè)量精度受幅度測(cè)量誤差的影響較大,。隨著數(shù)字技術(shù)的發(fā)展,，數(shù)字相位差測(cè)量技術(shù)被廣泛討論，但其都沒(méi)有論述數(shù)字化方法對(duì)相位差測(cè)量的影響和噪聲情況下相位測(cè)量的誤差分布,。本文提出的數(shù)字化相位差測(cè)量方法,，其基本思想是把信號(hào)轉(zhuǎn)換到頻率域，利用信號(hào)的相位譜直接完成在給定頻率點(diǎn)上相位差的測(cè)量,，且全面的分析了相位差測(cè)量誤差。
1 數(shù)字化寬帶測(cè)向系統(tǒng)模型
非均勻線陣的天線數(shù)為m,，天線的間距分別為d1,，d2，L dm-1寬帶入射信號(hào)分別為s(t),，入射方向與陣列法線的交角分別為θ,。
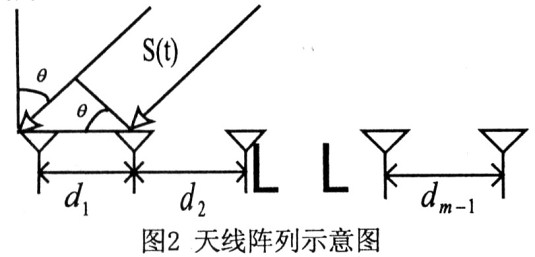
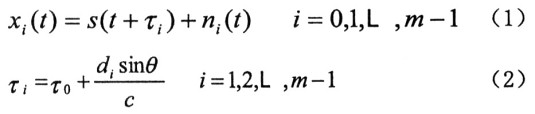
其中τ信號(hào)在第i個(gè)天線上相對(duì)于第O個(gè)天線的時(shí)間延遲，c是光速常數(shù),，di(l=1,，2，L,，m一1)為天線間距,。對(duì)式(2)兩邊同做傅立葉變換：
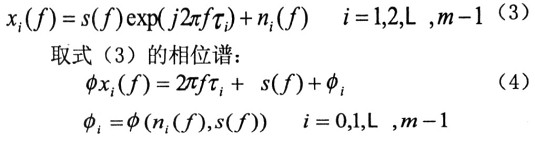
式(4)中φs(f)表示信號(hào)s的相位譜；φi為由噪聲譜對(duì)信號(hào)相位譜影響產(chǎn)生的誤差,。作如下的相位差變換：
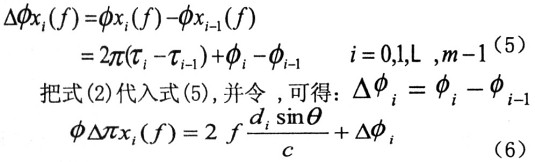
式(6)中相位差△φxi(f)是無(wú)模糊的相位差,。然而實(shí)際中由于天線陣列的間距大于半波長(zhǎng)因而相位差是有模糊的。
不妨令：
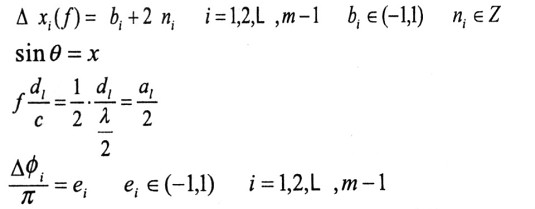
式中bi是有模糊的相位差,，ni表示模糊整數(shù),，ai為相對(duì)基線長(zhǎng)度，ei為相位差誤差,。則式(6)可代換為：
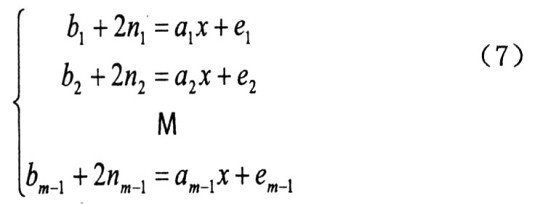
這是數(shù)字化寬帶測(cè)向系統(tǒng)模型,。
以下的工作都是圍繞這個(gè)模型展開(kāi)。其一是如何測(cè)量相位差bi(i=1，2,，L,，m一1) 及推導(dǎo)相位差測(cè)量誤差ei(i=l，2,，L,，m一1)的分布密度函數(shù)。其二是如何快速求解模糊整數(shù)ni(i=1,，2,，L，m一1),，即快速解模糊問(wèn)題,，這將在第二篇論文中討論。其三是如何求解x的最優(yōu)估計(jì)值從而獲得測(cè)向角θ=arcsin(x),，并進(jìn)行測(cè)向角測(cè)量誤差分析,；同時(shí)還會(huì)討論如何進(jìn)行天線陣列的設(shè)計(jì)問(wèn)題，即如何選取天線間隔d1,，d2,，L dm一1使得式(7)在概率意義下有唯一不模糊解，這些都將在第三篇論文中討論,。
2 數(shù)字化相位差測(cè)量及數(shù)字化方法誤差
不妨設(shè)兩個(gè)通道的時(shí)延為τ,，信號(hào)為△t，信號(hào)持續(xù)時(shí)間為s(t),，采樣間隔為N,，采樣點(diǎn)數(shù)為T。
式(14)即為相位差測(cè)量的數(shù)字化方法誤差函數(shù),。
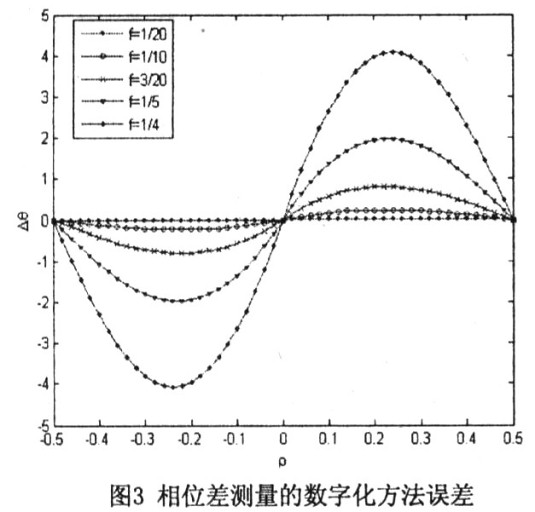
從圖3中可以看出：在f=1／4,，即采樣頻率是所測(cè)頻率的4倍時(shí)，相位差最大誤差約為40,；當(dāng)采樣頻率是所測(cè)頻率的20倍時(shí),，方法誤差可以忽略。
3通道高斯白噪聲引起的信號(hào)相位誤差設(shè)通道噪聲是高斯白噪聲N(O,，σ2),，采樣點(diǎn)數(shù)為N。則有：(1)其在離散傅立葉變換序列的實(shí)部序列和虛部序列是獨(dú)立同分布的高斯白噪聲序列(證明略),。(2)噪聲的幅度譜服從瑞利分布,，相位譜服從均勻分布(證明略)。(3)噪聲對(duì)信號(hào)相位譜的影響,。
圖4中,，R為信號(hào)頻譜幅度值,，r，θ為噪聲頻譜幅度值和相角,，w為噪聲引起的信號(hào)相位誤差,。
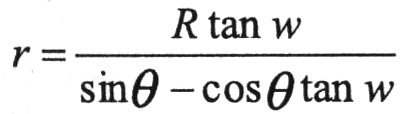
令θ’=θ，則有：
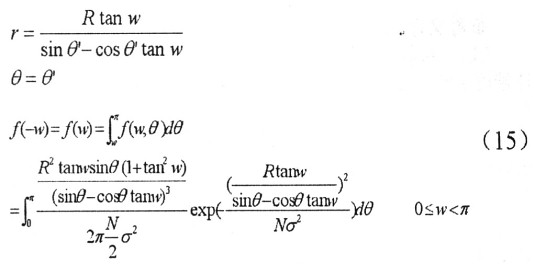
設(shè)噪聲的歸一化帶寬為B,，信號(hào)的幅度一致性系數(shù)為ρ,，白噪聲功率為σ2，信噪比為SN,，則計(jì)算噪聲對(duì)信號(hào)的相位譜的影響關(guān)系,。其中ρ義為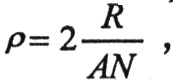
通過(guò)簡(jiǎn)單證明可得的零直流分量信號(hào)的幅度一致性系數(shù)ρ≤1。則：
式(16)即為噪聲引起的相位誤差分布密度函數(shù),。
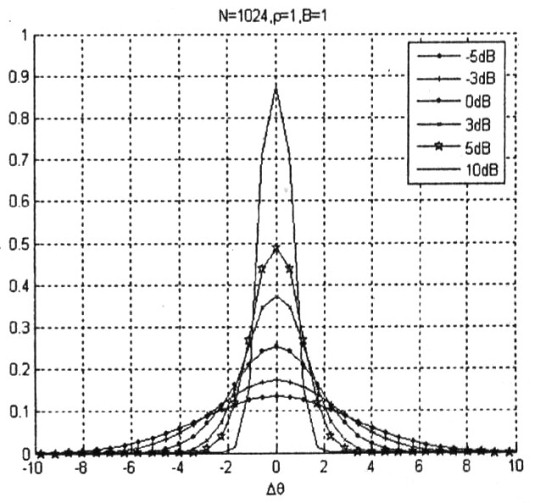
圖6噪聲引起的相位誤差分布密度函數(shù)和信噪比的關(guān)系
圖6中顯示,，由通道高斯白噪聲引起的信號(hào)相位誤差分布近似于高斯分布。
4 結(jié)束語(yǔ)
本文主要給出了數(shù)字化寬帶測(cè)向系統(tǒng)模型(式(7))和數(shù)字化相位差測(cè)量的原理公式(式(13)),，推導(dǎo)了相位差測(cè)量的數(shù)字化方法誤差函數(shù)(式(14))和由通道高斯白噪聲引起的信號(hào)相位誤差分布密度函數(shù)(式(16)),。