??? 摘 要： 石英晶體" title="石英晶體">石英晶體微天平（QCM）信號采集系統(tǒng)的設(shè)計質(zhì)量是影響其測量精度的重要因素,。提出了一種QCM信號在線采集系統(tǒng)的實現(xiàn)方案,，給出了系統(tǒng)的結(jié)構(gòu)框圖,，并對系統(tǒng)電路進行了詳細(xì)的分析,。
??? 關(guān)鍵詞： 石英晶體微天平? DSP? 諧振頻率
?
??? QCM(Quartz Crystal Microbalance)是由AT切石英晶體片和鍍在其上下表面的金屬電極構(gòu)成的一種諧振式傳感器,。其結(jié)構(gòu)如圖1所示,。QCM作為微質(zhì)量傳感器具有結(jié)構(gòu)簡單" title="結(jié)構(gòu)簡單">結(jié)構(gòu)簡單,、成本低,、振動Q值大、靈敏度高,、測量精度可以達(dá)到納克量級的優(yōu)點,，被廣泛應(yīng)用于化學(xué)、物理,、生物,、醫(yī)學(xué)和表面科學(xué)等領(lǐng)域中[1],，用以進行氣體、液體的成分分析以及微質(zhì)量的測量,、薄膜厚度的檢測等,。根據(jù)需要，還可以在金屬電極上有選擇地鍍膜,，進一步拓寬其應(yīng)用,。例如，若在電極表面加一層具有選擇性的吸附膜,可用來探測氣體的化學(xué)成分或監(jiān)測化學(xué)反應(yīng)的進行情況[2],。若選用生物活性膜,則可制成生物傳感器,如質(zhì)量式的基因傳感器等[3],。隨著生物科學(xué)的蓬勃發(fā)展，QCM作為基因傳感器在生物領(lǐng)域的應(yīng)用有著廣闊前景,。
?
??? 在國外，QCM在氣相中的應(yīng)用已經(jīng)相當(dāng)成熟,，近幾年,，對液相中的QCM應(yīng)用的研究也取得了很大進步，并且已經(jīng)出現(xiàn)了很多商品化的產(chǎn)品,，但是它們的價格非常昂貴,。國內(nèi)的相關(guān)研究相對較少。本文提出了一種基于DSP的QCM信號在線采集系統(tǒng),。該系統(tǒng)主要由高頻信號發(fā)生器,、QCM傳感器和信號采集處理部分組成，結(jié)構(gòu)簡單,、成本低,。借助DSP強大的數(shù)字信號處理功能，實現(xiàn)了在線測量,，并且保證了較高的測量精度,。
1 QCM測量原理
??? 石英是具有壓電性質(zhì)的物質(zhì)之一，當(dāng)外加交變電壓的頻率為某一特定頻率時,，石英晶片振幅會急劇增加,這就是壓電諧振,。
??? 1959年Sauerbrey在假定外加質(zhì)量均勻剛性地附著于QCM的金電極表面的條件下，得出了QCM的諧振頻率" title="諧振頻率">諧振頻率變化與外加質(zhì)量成正比的結(jié)論,。即：
??? 
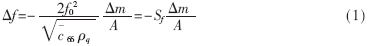
??? 式中,，Δf為QCM諧振頻率的變化；f0為QCM的基頻,；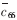
為石英的壓電強化剪切模量,；ρq為石英的密度：2.651g/cm3；A為金電極的面積,；Sf為傳感器的靈敏度,；Δm為電極表面的質(zhì)量變化,。通過（1）式可得到QCM電極表面的質(zhì)量變化。由于QCM的靈敏度很高,，可以達(dá)到納克級,，并且結(jié)構(gòu)簡單，因此一問世就得到了廣泛的應(yīng)用,，如用于真空或空氣中膜的厚度檢測等。
??? 20世紀(jì)90年代以來,，隨著研究的深入,，QCM在液相中也取得了廣泛的應(yīng)用，主要用于生物,、化學(xué)等領(lǐng)域的檢測中,。1982年Monura和Okuhara最先提出了可以在液相中驅(qū)動QCM振動的電路，將QCM的應(yīng)用擴大到了液相,。1985年Kanazawa和Gordon推出了QCM在牛頓流體中振蕩時其諧振頻率變化與液體的粘度和密度的關(guān)系式[4],，即：
??? 
??? 從式(1)、(2)可以看出,，QCM諧振頻率的變化量Δf是關(guān)鍵的待測量,。
2 系統(tǒng)方案
??? 目前驅(qū)動QCM振動并采集其輸出信號的方法主要有兩種：（1）振蕩電路法；（2）頻譜分析" title="頻譜分析">頻譜分析法,。振蕩電路法的基本原理為：將QCM接入自激振蕩電路中,，使其構(gòu)成選頻元件，電路的振蕩頻率等于QCM的諧振頻率,。通過電路振蕩頻率的變化可得到QCM諧振頻率的變化,，從而可推測出待測物質(zhì)性質(zhì)的變化。頻譜分析法的基本原理為：掃描QCM在其諧振頻率附近的一段頻率范圍內(nèi)的頻譜（幅頻和相頻特性）,，通過該頻譜可得到QCM的諧振頻率,、Q值等參數(shù)。與振蕩電路的方法相比,，頻譜分析的主要優(yōu)點有：在大阻尼介質(zhì)中不會停振,、測量結(jié)果信息量大、形象直觀,、計算解釋容易,。本設(shè)計給出了一種基于頻譜分析法的QCM信號采集系統(tǒng)，其電路原理框圖如圖2所示,。
?
3 系統(tǒng)分析
??? 電路的正弦信號產(chǎn)生部分由直接數(shù)字信號合成（DDS）芯片,、自動增益控制（AGC）和運放（AMP）等組成。DDS接收DSP的控制信號，產(chǎn)生頻率可控的正弦信號,；AGC調(diào)整DDS的輸出信號,，使其峰-峰值始終保持為一個已知的定值；AMP則完成信號的放大和阻抗轉(zhuǎn)換,。由于信號產(chǎn)生部分增加了自動增益控制使其產(chǎn)生的信號的峰-峰值保持恒定,，從而減少了待測信號的數(shù)目，簡化了測量和處理的過程,。
??? 信號產(chǎn)生器部分產(chǎn)生的正弦信號作用在如圖2中所示的兩個反相" title="反相">反相比例電路上,，反相比例電路的輸出信號包含QCM在相應(yīng)頻率下的等效阻抗的幅值和相角信息。根據(jù)反相比例電路虛地的原理,，作用在QCM上的電壓始終保持為信號產(chǎn)生部分的輸出電壓與地之間的電壓差,。采用這種結(jié)構(gòu)的好處是：（1）使作用在QCM上的電壓保持恒定，簡化了處理過程,。（2）只通過一個反相比例電路的輸出信號即可單獨得到QCM等效阻抗的幅值（通過后面的計算將會得到此結(jié)論）,。
??? 反相比例電路輸出信號的采集和處理部分的核心是兩個乘法器和低通濾波器。設(shè)信號產(chǎn)生部分的輸出信號電壓為：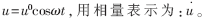
則含有QCM的反相比例電路的輸出為：
??? 
式中,，R1為參考電阻R1的阻值,，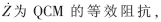
|Z|和φ為其對應(yīng)的幅值和相角。另一個反相比例電路的輸出為：
??? 這兩個直流信號經(jīng)過放大器放大后由ADC芯片采集,，所采集的數(shù)字信號經(jīng)DSP處理后送往PC機供分析、顯示之用,。為保證采集的精度,，此處的放大器選用AD620芯片。AD620具有高精度,、低漂移和低噪聲的優(yōu)點,另外AD620可以通過一個外接電阻方便地調(diào)節(jié)放大倍數(shù),。ADC芯片采用雙通道的高精度轉(zhuǎn)換芯片。
??? 整理（3）,、（4）兩式可得QCM等效阻抗的幅值為：
??? 
??? 上面各式中R1,、R2,、R3和u0均為與電路參數(shù)有關(guān)的已知值,所以由采集的信號uf 1和uf 2,，通過(5)、(6)式即可分別計算出QCM等效阻抗的幅值和相角,。通過DDS改變產(chǎn)生信號的頻率,，即可得到不同頻率下QCM等效阻抗的幅值和相角。對QCM諧振頻率附件的頻率段進行掃描,，記錄每個頻率測量點對應(yīng)的幅值和相角，即可繪出QCM的頻譜,。由頻譜可以得出QCM諧振頻率的變化量Δf,。
??? 由(5)式可知，通過uf1即可單獨求出QCM等效阻抗的幅值,，得到QCM的幅頻特性曲線,。因此本電路可以設(shè)定兩種工作模式：(1)使電路僅采集信號uf1，從而得到QCM的幅頻特性曲線,，由該曲線可以得到QCM的諧振頻率（對應(yīng)于阻抗值最低點處的頻率）,、帶寬,、Q值等參數(shù),。采用此模式得到的信號雖不全面，但它足以得到諧振頻率的變化量Δf,，且由于這種模式只采集,、處理一路信號，因此工作速度較快,。(2)同時采集信號uf1和uf2，從而可得到QCM的幅頻特性和相頻特性曲線,。采用此模式可以得到QCM的最全面的信息,，但它的工作速度與模式(1)相比較慢。
??? 數(shù)字信號的采集,、處理,、傳輸以及整個電路的控制是由DSP控制器、A/D轉(zhuǎn)換芯片和PC機完成的,。DSP的高速處理能力和較大的數(shù)據(jù)存儲空間使得系統(tǒng)可以在線地采集處理信號,。實際中,，從低通濾波器輸出的信號uf1,、uf2是混雜著噪聲的直流信號，為了消除引入的干擾信號,，在DSP中采用濾波算法對數(shù)據(jù)進行濾波處理,，可以進一步提高系統(tǒng)的精度。
??? 本系統(tǒng)結(jié)構(gòu)簡單,、成本低,、易于實現(xiàn)。通過使作用在QCM上的信號峰-峰值保持恒定,，簡化了后續(xù)的計算處理過程,。同時系統(tǒng)具有兩種工作模式，可采集的信息量全面。系統(tǒng)的核心控制器由DSP擔(dān)任,，借助DSP強大的數(shù)字信號處理能力,，可以實現(xiàn)信號在線采集，并對信號進行濾波處理,，進一步提高了系統(tǒng)精度,。
參考文獻
1 朱則善. 石英晶體微天平(QCM) 及其在電化學(xué)研究中的應(yīng)用[J].化學(xué)通報,1991(9):27～31
2 Antonio Arnau,Yolanda, Jimennez. An Ex2 tended Butterworth2Van Dyke Model for Quartz Crystal Microbalance Applications in Vis2 coelastic Fluid Media[J]. IEEE, 2001;48(5):1367～1381
3 劉建輝,莫志宏,劉明華. 基因傳感器研究新進展[J].國外醫(yī)學(xué)臨床生物化學(xué)與檢驗學(xué)分冊,2000;21(5):233～234
4 Keiji K.K., Gordon J.G. Frequency of a Quartz Microbalance in Contact with Liquid. Anal. Chem Acta,1985;59:99~104