隨著移動IP技術(shù)的發(fā)展,，IP組播系統(tǒng)需要動態(tài)的組播源或組播接收者的加入，現(xiàn)有的組播協(xié)議如DVMRP,、PIM-DM等基于靜態(tài)組播" title="靜態(tài)組播">靜態(tài)組播源和主機的協(xié)議都需要進行擴展^[1],。移動環(huán)境IP組播密鑰管理除了要解決靜態(tài)組播要解決的如：機密性、完整性,、認證,、同謀破解等網(wǎng)絡(luò)安全基本問題以外，還要解決前向加密,、后向加密,、密鑰生成計算量、密鑰發(fā)布占用帶寬,、密鑰發(fā)布延遲,、健壯性、可靠性,、抵制攻擊,、協(xié)議獨立等問題^[2～3],。近幾年來有很多組播協(xié)議被相繼提出，同時為了更加安全地通信,，也提出了一些基于移動IP的組播密鑰管理協(xié)議,。
　　本文就目前存在的移動IP組播密鑰協(xié)議進行研究，分析各個協(xié)議的優(yōu)缺點,，并對以后移動IP組播密鑰管理的發(fā)展發(fā)表自己的看法,。
1 基于樹形的密鑰管理協(xié)議
　　在這種密鑰管理拓撲結(jié)構(gòu)中，密鑰被分成兩種,，一種是組會話密鑰(group session key),，用來加密組成員之間的信息交換；另一種是組輔助密鑰(group auxiliary key)用來有效地分發(fā)和更新組會話密鑰,。
　　下面對幾種基于樹形的密鑰管理協(xié)議進行介紹和分析,。
1.1 簡單密鑰分發(fā)協(xié)議
　　由H. Hugh等提出^[4]，在這種協(xié)議中,，簡單密鑰分發(fā)協(xié)議中心是組控制器GC(Group Controller),，GC和每一個成員分別分享一個密鑰k_C,i并負責(zé)分發(fā)給M_i，組成員共享組密鑰K_G,，當一個新的成員M_N+1 加入時,，GC分配M_N+1共享密鑰k_C,N+1，然后GC需要把新的組密鑰k_G′用舊的組密鑰K_G加密并且組播給M₁,、M₂、…,、M_N,；用k_C,N+1加密單播給M_N+1。但是當一個成員離開時,，就不能用舊的組密鑰來加密新的組密鑰,，因為離開者知道舊密鑰，這時GC只能用與留下成員的共享密鑰分別加密新的組密鑰單播給相應(yīng)的成員,。很顯然,這種方式在組規(guī)模比較大的情況下,，成本是很昂貴的，需要N次加密和發(fā)送N次更新消息,。
1.2 利用密鑰圖表的組密鑰管理協(xié)議
　　C. K. Wong等提出了利用密鑰圖表的密鑰管理協(xié)議(Group Key Management Using Key Graphs)^[5],，這個協(xié)議通過密鑰圖表表示子組的安全方案" title="安全方案">安全方案。該協(xié)議定義了三種策略對成員加入/退出時更新密鑰的消息進行分組,，分別是面向用戶(user-oriented),、面向密鑰(key-oriented)和面向組(group-oriented)。
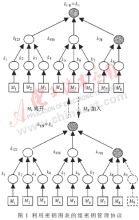
　　首先需要定義以下概念：一個安全的組可以用三元組(U,，K,，R)表示,。U是有限非空的組成員集合，K是有限非空的密鑰集合,，R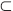U×K表示成員和密鑰的二元關(guān)系,。有兩個函數(shù)表示如下：keyset(M_i)={k|(M_i,k)∈R}，表示一組被Mi持有的密鑰,，并且keyset(Φ)=Φ;userset(k)={M_i|(M_i,k)∈R},表示一組持有密鑰k的成員,。拓撲圖如圖1所示。

　　(1) 面向用戶
　　在面向用戶方式中,，GC把M_i的新密鑰K_i^new作為單個密鑰更新消息并利用輔助密鑰加密后發(fā)送給M_i,，輔助密鑰被用來加密是由于它被最大" title="最大">最大的成員集合(U_max)共享，U={M_j∣K_j^new=K_i^new and I_j(keyset(M_j)-keyset(x))≠Φ, j=1,…,，N},，當x=Φ時表示有成員加入，x是退出發(fā)生時離開組的那個成員,。利用“最大”組的目的是為了最小化加密成本,，減少流量開銷，更新密鑰的消息通過組播發(fā)出,，這些消息只能被持有正確輔助密鑰的成員解密,。

　　(2)面向密鑰
　　對于一個組來說，一旦加入或離開發(fā)生,，一系列決定性的密鑰更新相應(yīng)地發(fā)生了,。在面向密鑰方式中，每一個更新密鑰消息包含一個單一的新密鑰,。為最小化加密成本,，GC將選擇一個輔助密鑰去加密一個密鑰更新消息，更新盡可能多的持有這個輔助密鑰的成員,。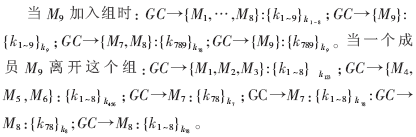

　　(3)面向組
　　在這種方式中,，GC試圖允許一個密鑰更新消息包含與新密鑰盡可能一樣多的新密鑰。新密鑰被適當?shù)淖咏M密鑰加密,，這樣做的目的是盡量把加密的成本降到最低,。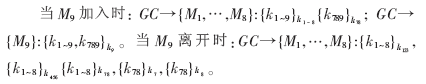

　　相對于SKDC方式，該方法加密成本大大降低,。全組維持密鑰的所有數(shù)目為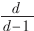n=N-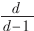,，每一個成員持有的密鑰數(shù)量為h=log_dN+1，h是密鑰樹的高度,，d是層數(shù),，N是組成員數(shù)目。GC需要維持O(N)個密鑰,，每一個成員存儲O(log_dN)個密鑰,。與SKDC相比,，這種方法的復(fù)雜性無論在加密還是密鑰更新消息時，成本與成員數(shù)目N是成比例的,；同時,，面向組充分提高了密鑰分發(fā)和管理的可伸縮性。
1.3 布爾函數(shù)最小化技術(shù)組密鑰管理協(xié)議
　　布爾函數(shù)最小化技術(shù)BFMT(Boolean Function Minimization Techniques)由Chang等提出^[6],。該方法為每一個用戶定義一個用戶ID,，這個UID由n比特的二進制字符串組成，一個用戶的密鑰系列整個由它的UID決定,。既然任何兩個用戶必須持有至少一比特不同的UID,，當它們中一個離開組播組時，其他的用戶可以通過收到離開用戶不持有的密鑰加密密鑰更新消息,。
　　全組維持n個輔助密鑰對：k_i和,，(i=0，…,，n-1),，每個密鑰對對應(yīng)UID中的一個比特。除了組會話密鑰kG以外,，每個密鑰還被分配n個密鑰,，例如，成員Mj持有密鑰ki,，如果它的UID的第i個比特是“1”,，或者它持有ki；如果它的UID的第i個比特是“0”,，一個UID和對應(yīng)的密鑰分配表示如圖2所示,。

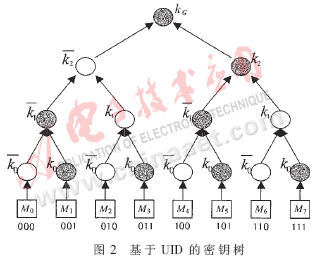
　　組會話密鑰k_G在根節(jié)點處，輔助密鑰k_i和作為內(nèi)部節(jié)點的密鑰,，而成員M_j是它的葉子,。圖2中每一個成員都有一個UID,，例如成員M₅的UID是“101”,，表明它擁有輔助密鑰k₂、和k₀,，另外還有每個成員都共享的密鑰kG,，每一個成員的密鑰由它到根的路徑表示。
　　一般情況下,，每個成員的離開都導(dǎo)致k_G和輔助密鑰的更新,，所以離開的成員不能解密以后的通信內(nèi)容。利用定量的方法,，組的變化定量,、密鑰更新過程根據(jù)指定的時間超時進行,，這個過程被稱為一個“巡回”(round)。對于第r個“巡回”,，組會話密鑰表示為kG(r),，輔助密鑰表示為k_i(r)和(r)。
　　(1)刪除單個成員
　　在第r個“巡回”,，有一個成員離開時,，為了更新密鑰k_G(r)，GC計算新的會話密鑰k_G(r+1),。新的密鑰利用與離開成員“互補”的密鑰加密,。如在圖3中，假如M₅離開組,，“互補”密鑰是,，那么k_G(r+1)就可以使用這三個密鑰加密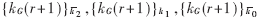并組播給所有的組成員。由于M₅不知道這些密鑰中的任何一個,，所以它不能解密組播的更新密鑰信息而得到新的會話密鑰,。另一方面，任何一個成員,，它的UID至少有一個比特與M₅不同,，因此持有的keyset(M_j)使得∩keyset(M_j)≠Φ，其中j≠5,。這樣就確保了其他的任何一個成員至少能解密一個密鑰更新的數(shù)據(jù)塊,。
　　為了保證離開的成員不能利用它的輔助密鑰解密以后的會話密鑰更新，輔助密鑰利用單向hash函數(shù)f進行更新：k_i(r+1)=f(k_i(r),k_G(r+1)),。

　　(2)刪除多個成員
　　為了最小化密鑰更新消息加密的成本,，最值得做的是定時地成批刪除組成員。在圖2中,，不失一般性,，假設(shè)M0和M4離開組，沒有定量的情況下,，一共需要2×3=6個消息需要發(fā)出,，因為在兩輪中每次都需要使用3個輔助密鑰用來加密發(fā)送的消息。在成批刪除時,，利用布爾算法計算M₀和M₄都擁有的輔助密鑰S,，在這個例子中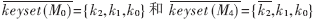，,，所以S={k₁,k₀}=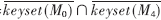,。那么利用S加密新的會話密鑰可以確保任何一個離開的成員不能算出新的會話密鑰k_G(r+1)，而所有剩余的成員可以正確計算出來。
　　當M₀和M₄離開時,，可以借助布爾函數(shù)最小化技術(shù)計算S,，相應(yīng)的布爾成員函數(shù)和它的最小化成員函數(shù)Karnaugh圖被表示出來。
　　這個方法具有以下特點：第一,， 采用了最普通的二進制算法,，所以很容易理解；簡化了密鑰更新產(chǎn)生和分發(fā)算法,，僅僅計算離開成員互補密鑰S,，密鑰更新組播消息僅僅一次；對于加密成本,，最大成本是O(n)=O(logN),，n是輔助密鑰對的數(shù)目，所以用n比特代替所有N個用戶已經(jīng)足夠了,。第二,，它提出了定量更新密鑰的思想，從布爾算法中找到了最小化技術(shù),，有效解決了最少成員加密問題,。但是，它還沒有提供一個滿意的方式去控制高成本,，這種成本和組規(guī)模N成比例,，O(N)復(fù)雜性可能嚴重地影響這種方法的可伸縮性。
1.4 單向函數(shù)樹的組密鑰管理協(xié)議
　　單向函數(shù)樹OWFT(One-Way Function Trees)由McGrew 等提出^[7],，這種方法在組成員變化時基于單向函數(shù)樹來建立組會話密鑰,。
　　在這個方法里，GC維持著二叉樹,，所有的組成員在葉子節(jié)點上,，但葉子不一定都是成員，每一個節(jié)點x (包括葉子)有兩個關(guān)聯(lián)的密鑰：一個unblinded 節(jié)點密鑰k_x和一個blinded節(jié)點密鑰k′_x,，它們由著名的單向函數(shù)g和一個“混合” 函數(shù)f計算得到：k_x=f(g(k_left(x)),g(k_right(x)))=f(k′_left(x),k′_right(x)),， 式中l(wèi)eft(x)和right(x)表示x的左邊和右邊子節(jié)點。根據(jù)這個規(guī)則,，借助于節(jié)點的unblinded 密鑰和其兄弟節(jié)點的blinded密鑰得出其父節(jié)點的unblinded密鑰,。
　　密鑰更新說明如下：
　　(1)添加一個成員
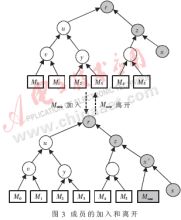
　　當一個成員M_new加入時，GC做的就是挑選一個葉子節(jié)點x,，用擁有兩個節(jié)點的一個新的內(nèi)部節(jié)點x′代替,，其中一個子節(jié)點是x本身,，另一個是新加入的M_new,如圖3所示,。受影響的節(jié)點子組用灰色表示，因此，那些灰色節(jié)點的unblinded密鑰需要更新以實現(xiàn)后向保密,。
　　為了計算新的組會話密鑰,，存儲舊版本blinded密鑰的節(jié)點應(yīng)該被通知更新它們的新版本。例如,，節(jié)點y應(yīng)該得到節(jié)點z的最新blinded密鑰k′_z,，需要得到密鑰k′_z的節(jié)點集合是S_z={u,v,y,M₀,M₁,M₂,M₃}，包括z的兄弟節(jié)點u和u的所有派生節(jié)點,。這個新的blinded 密鑰k′_z被u的unblinded密鑰k_u加密后包含在一個密鑰更新消息中組播給S_z,。
　　(2)刪除一個成員
　　圖3表示當一個成員M_new離開時，節(jié)點x′被刪除并被節(jié)點x代替,，所有從節(jié)點x到根r的密鑰被更新,。同樣，當一個成員加入時,，最新的blind密鑰被安全地傳輸給那些存儲舊版本密鑰的節(jié)點,。
　　OWFT最新穎之處是提高了密鑰管理的可伸縮性，因為它通過維護一個單向函數(shù)樹和每個成員獨立計算組密鑰把會話密鑰直接傳送出去,，更新密鑰消息的數(shù)量和加密復(fù)雜性取決于需要更新blinded密鑰子組的數(shù)量,。既然blinded密鑰更新的最大數(shù)量是h(樹的高度)，那么密鑰更新組播消息和加密成本一樣都是O(h)=O(logN),。McGrew等給出系統(tǒng)存儲的密鑰數(shù)量為O(N),，每個成員存儲的密鑰數(shù)量為O(logN)。
　　但是,，GC不得不維持2N-1個子組成員的信息,，因為每一個樹中的節(jié)點對應(yīng)于一個包含它自己和由它所派生節(jié)點的子組，價值不高并強加給GC的工作影響這個算法應(yīng)用在大規(guī)模組時的可伸縮性,。
　　以上三個樹形的密鑰管理協(xié)議比較如表1所示,。

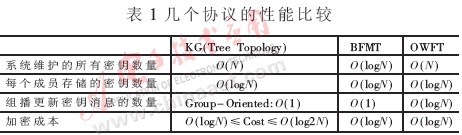
2 其他密鑰管理協(xié)議
　　除了以上提到的幾個密鑰管理協(xié)議，其他的還有很多,。Iolus協(xié)議是一個分布式等級樹的典型方法,、W. Waldogel等提出的LKH+(logical key hierarchy)協(xié)議、A. Perrig 等提出了ELK協(xié)議,、S.Rafaeli等提出的EHBT(efficient hierarchical binary tree)協(xié)議等,。
　　本文比較了一些協(xié)議的優(yōu)點和不足，代表了目前這個研究領(lǐng)域的研究成果,。目前還沒有一個公認的都能接受的合適的協(xié)議,。關(guān)于組播密鑰管理最主要的問題是可伸縮性，有些協(xié)議利用分等級的方法有較好的可伸縮性,，是這個領(lǐng)域以后發(fā)展的一個重要方向,。
參考文獻
1 孫利民. 移動IP技術(shù)[M].北京：電子工業(yè)出版社，2003：202～230
2 徐明偉.組播密鑰管理的研究進展[J].軟件學(xué)報，2004;15(1)：141～150
3 C.Boyd,A.Mathuria. Key Establishment Protocols for Secure Mobile Communications:A Selective Survey. Information Security and Privacy, LNCS 1438, Springer Verlag,1998：344～355
4 Harney Hugh, Carl Muckenhirn, Thomas Rivers. Group Key Management Protocol Architecture, Request for comments(RFC) 2093, Internet Engineering Task Force,March 1997
5 C. K. Wong, M. Gouda.Secure Group Communications Using Key Graphs. S. S. Lam, Department of Computer Sciences,University of Texas at Austin, Technical Report 97～23,July 28, 1997
6 I. Chang, R. Engel, D. Kanlur, D. Pendarakis,etc. Key Management for Secure Internet Multicast using Boolean Function Minimization Techniques. IEEE Infocomm,，1999
7 David A. McGrew, Alan T. Sherman. Key establishment in large dynamic groups using one-way function trees.Technical Report 0755,TIS Labs at Network Associates, Inc.,Glenwood, MD, May 1998(收稿日期：2005-02-21)