1 引言

　　隨著數(shù)字技術(shù)的快速發(fā)展，數(shù)字信號處理已深入到各個學(xué)科領(lǐng)域,。在數(shù)字信號處理中,，許多算法如相關(guān)、濾波,、譜估計,、卷積等都可通過轉(zhuǎn)化為離散傅立葉變換(DFT)實現(xiàn)，從而為離散信號分析從理論上提供了變換工具,。但DFT計算量大,，實現(xiàn)困難?？焖俑盗⑷~(FFT)的提出,，大大減少了計算量，從根本上改變了傅立葉變換的地位，成為數(shù)字信號處理中的核心技術(shù)之一,，廣泛應(yīng)用于雷達(dá),、觀測,、跟蹤,、高速圖像處理、保密無線通信和數(shù)字通信等領(lǐng)域,。

　　目前,，硬件實現(xiàn)FFT算法的方案主要有：通用數(shù)字信號處理器(DSP)、FFT專用器件和現(xiàn)場可編程門陣列(FPGA),。DSP具有純軟件實現(xiàn)的靈活性,，適用于流程復(fù)雜的算法，如通信系統(tǒng)中信道的編譯碼,、QAM映射等算法,。DSP完成FFT運(yùn)算需占用大量DSP的運(yùn)算時間，使整個系統(tǒng)的數(shù)據(jù)吞吐率降低,，同時也無法發(fā)揮DSP軟件實現(xiàn)的靈活性,。采用FFT專用器件，速度雖能夠達(dá)到要求,。但其外圍電路復(fù)雜,，可擴(kuò)展性差，成本昂貴,。隨著FPGA發(fā)展,，其資源豐富，易于組織流水和并行結(jié)構(gòu),，將FFT實時性要求與FPGA器件設(shè)計的靈活性相結(jié)合,，實現(xiàn)并行算法與硬件結(jié)構(gòu)的優(yōu)化配置，不僅可以提高處理速度,，并且具有靈活性高,。開發(fā)費(fèi)用低、開發(fā)周期短,、升級簡單的特點,。針對某OFDM系統(tǒng)中FFT運(yùn)算的實際需要，提出了基于FPGA的設(shè)計來實現(xiàn)FFT算法,，并以16位長數(shù)據(jù),，64點FFT為例，在QuartusⅡ軟件上通過綜合和仿真,。

　　2 FFT原理及算法結(jié)構(gòu)

　　FFT是離散傅立葉變換(DFT)的快速算法,。對于N點離散的有限長時問序列x(n)，其傅里葉變換為：

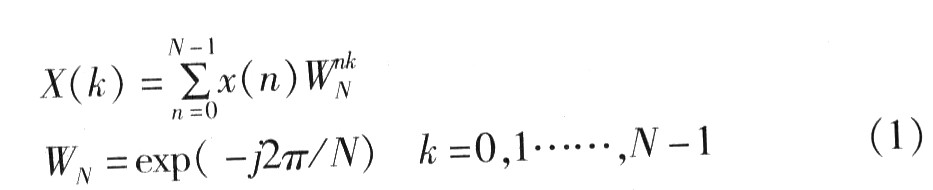
　　完成N點的DFT需要N2次復(fù)數(shù)乘法和N(N-1)次復(fù)數(shù)加法。點數(shù)大時,，計算量也大,，所以難以實現(xiàn)信號的實時處理。FFT的基本思想是利用旋轉(zhuǎn)因子WN的周期性,、對稱性,、特殊性以及周期N的可互換性，將長度為N點的序列DFT運(yùn)算逐次分為較短序列的DFT運(yùn)算,，合并相同項,，大大減少了計算量。

　　FFT算法分為兩大類：一類是針對N=2的整數(shù)次冪的算法,，如基2算法,、基4算法、實因子算法和分裂算法等：另一類是N≠2的整數(shù)次冪算法,，以winograd為代表的一類算法,。硬件實現(xiàn)時，不僅要考慮算法運(yùn)算量的大小,，而且要考慮算法的復(fù)雜性和模塊化,。控制簡單,、實現(xiàn)規(guī)整的算法在硬件系統(tǒng)中要優(yōu)于僅降低運(yùn)算量的算法?，F(xiàn)有FFT算法的FPGA設(shè)計方案基本上都是針對于第一類算法，而第二類算法盡管有其重要的理論價值,，但硬件不易實現(xiàn),。由于該設(shè)計點數(shù)不是太多，綜合考慮FFT處理器的面積和成本,。所以采用按時間抽取的基2快速傅立葉算法(基2DIT-FFT),。

　　對于長度為N=2m的序列x(n)，其中m是整數(shù),，將x(n)按奇偶分成兩組,，即令：n=2r和n=2r+1，而r=0,，1,，…，N/2-1,，于是：

　　所以A(k)和B(k)可完整表示X(k),。依次類推，可一直向前追溯到2點的FFT,，這樣整個N點的FFT算法分解成log 2N級運(yùn)算,，每級有N／2個基2碟形運(yùn)算,。圖1是N=8的DIT-FFT運(yùn)算流圖。

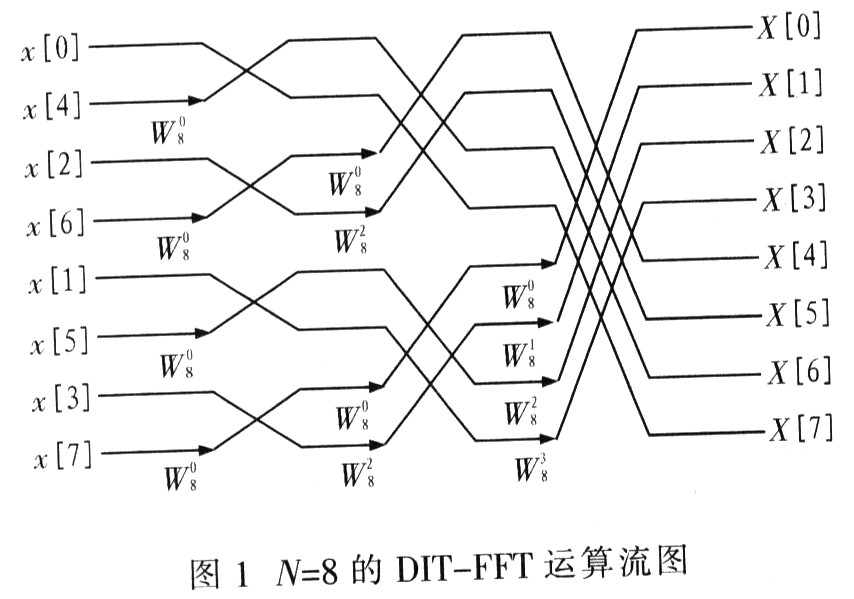
　　3 FFT處理器的結(jié)構(gòu)設(shè)計

　　FFT實現(xiàn)的設(shè)計方案有順序處理,、級聯(lián)處理,、并行處理和陣列處理。順序處理每次運(yùn)算僅用一個蝶形單元,處理方式簡單,，運(yùn)算速度較慢,。級聯(lián)處理、并行處理和陣列處理的速度較快,，但占用資源較多,?？紤]到該設(shè)計運(yùn)算點數(shù)較少,，因此采用改進(jìn)的順序處理方案，在原有順序處理的基礎(chǔ)上對FFT處理過程中數(shù)據(jù)傳輸進(jìn)行控制,。使得該結(jié)構(gòu)在繼承原有順序處理電路簡單,、占用資源較少優(yōu)點同時又兼有級聯(lián)處理運(yùn)算速度較快的優(yōu)點。采用自頂向下的方法對處理器模塊化,，其結(jié)構(gòu)框圖如圖2所示,。

　　4 模塊設(shè)計與綜合仿真

　　整個FFT處理器是由存儲器、蝶形運(yùn)算單元,、旋轉(zhuǎn)因子單元,、控制單元和數(shù)據(jù)控制單元組成，各個單元通過控制單元產(chǎn)生的控制和使能信號進(jìn)行工作,。

　　4．1 蝶形運(yùn)算單元

　　蝶形運(yùn)算單元是整個FFT處理單元的重要部分,，直接影響整個FFT單元性能?；?時間抽取的蝶形信號流程圖如圖3所示,，p和q為數(shù)據(jù)序號，xm(p))和xm(q)是第m級蝶形運(yùn)算的輸入,，xm+1(p)和xm+1(q)是該蝶形運(yùn)算的輸出,，WrN為相應(yīng)的旋轉(zhuǎn)因子。

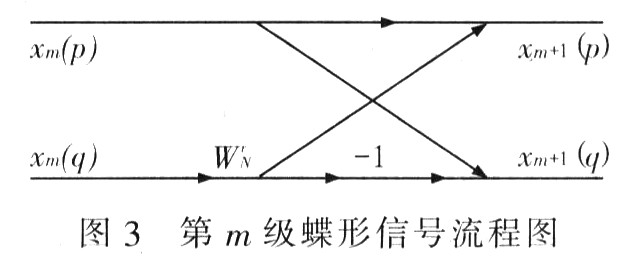
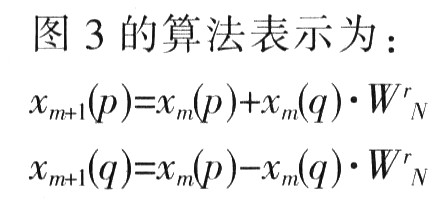
　　由上式看出,，一個基2蝶形運(yùn)算要進(jìn)行1次復(fù)乘,、2次復(fù)加。為了提高運(yùn)算速度采用并行運(yùn)算,，采用4個實數(shù)乘法器,、3個實數(shù)加法器和3個實數(shù)減法器組成。設(shè)輸入數(shù)據(jù)：x1=x1_r+jx1＿im,，x2=2＿r+jx2＿im,，旋轉(zhuǎn)因子為WrN=c-jd，則輸出y1=y1_r+jy1_im和y2=y2_r+jy2＿im。實現(xiàn)蝶型運(yùn)算單元如圖4所示,。

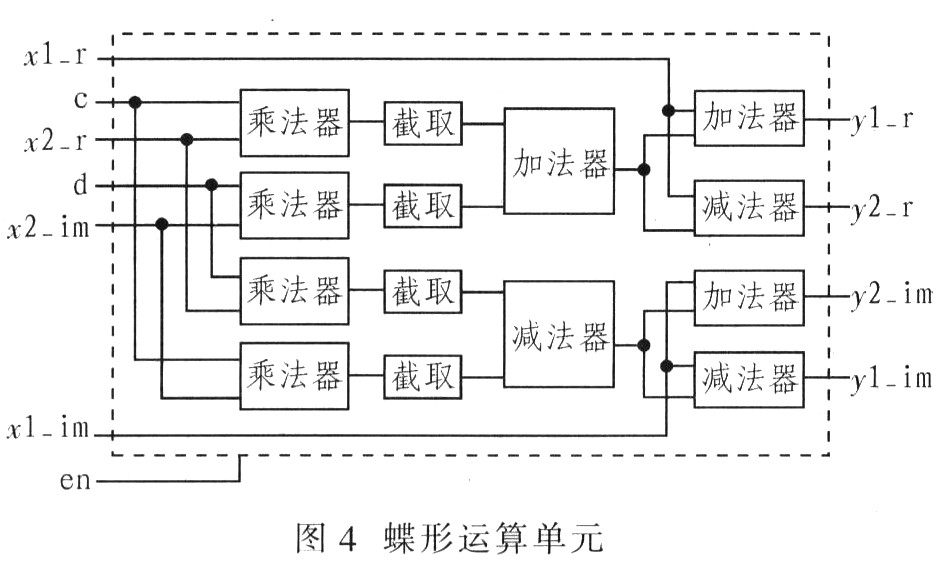
　　數(shù)據(jù)格式選擇定點16位二進(jìn)制補(bǔ)碼,。設(shè)計時必須考慮乘法器速度，將會直接影響整個FFT處理單元的運(yùn)算速度,該設(shè)計的乘法器利用QuartusⅡ開發(fā)軟件中所提供的宏單元生成,。乘法器的兩輸入均為16位,，輸出32位。因為乘法器中帶有旋轉(zhuǎn)因子項．所以乘法運(yùn)算后不應(yīng)改變輸入的幅值即乘法器的輸出仍為16位,，因此要對輸出數(shù)據(jù)進(jìn)行截取,，截取其中16位作為加(減)法器的輸入。

　　4．2 存儲單元

　　在FFT處理單元中存儲器是必不可少的單元,，蝶形運(yùn)算數(shù)據(jù)的輸入輸出和中間結(jié)果的存儲都要經(jīng)過存儲器,，因此它們的頻繁讀寫操作對整個FFT處理速度影響較大。圖2中存儲器A和存儲器B由RAM和狀態(tài)機(jī)組成,，各自分別具有數(shù)據(jù)總線,、地址總線和觸發(fā)時鐘。存儲器A接收外部輸入數(shù)據(jù),，存儲器B是中間結(jié)果單元,，除第一級蝶形運(yùn)算外每級數(shù)據(jù)的輸入輸出均經(jīng)過該存儲器。在兩塊存儲器和蝶形運(yùn)算模塊之間加入兩個數(shù)據(jù)控制器配合工作,，可以在寫入上一組中間結(jié)果的同時讀取下一組蝶形運(yùn)算數(shù)據(jù),，從而提高FFT的處理速度。

　　4．3 旋轉(zhuǎn)因子單元

　　旋轉(zhuǎn)因子單元是用于存儲FFT運(yùn)算所需的旋轉(zhuǎn)因子WrN=exp(-j2πr／N),。在Matlab中旋轉(zhuǎn)因子分為實部和虛部產(chǎn)生,，由于它們是小于1的小數(shù)，故在設(shè)計中需將其定點化,。其過程是將旋轉(zhuǎn)因子擴(kuò)大214倍,。取整數(shù)部分轉(zhuǎn)化為16位定點數(shù)，以．hex文件格式保存,，利用QuartusⅡ軟件的Megawizard工具設(shè)計,。ROM，并將．hex文件同化在其中,。根據(jù)旋轉(zhuǎn)因子的對稱性和周期性,，在利用ROM存儲旋轉(zhuǎn)因子時，可以只存儲旋轉(zhuǎn)因子表的一部分,，通過地址的改變查詢出每級蝶形運(yùn)算所需的旋轉(zhuǎn)因子,。

　　4．4 控制單元

　　控制單元用于協(xié)調(diào)驅(qū)動各模塊，在FFT運(yùn)算中具有關(guān)鍵作用,。存儲器A,、旋轉(zhuǎn)因子單元及數(shù)據(jù)控制器的讀信號,，存儲器B的讀寫信號都是由控制單元產(chǎn)生?？刂茊卧ㄟ^一個有限狀態(tài)機(jī)(FSM)實現(xiàn),，使用兩個內(nèi)部計數(shù)器控制狀態(tài)機(jī)的翻轉(zhuǎn)?？刂茊卧哂袉为?dú)的輸入時鐘,，可產(chǎn)生相應(yīng)的控制信號。

　　4．5 綜合仿真

　　選用Altera公司的QuartusⅡ軟件作為開發(fā)平臺,，以Stratix系列中的EP1S25型FPGA為核心器件,，采用白頂向下的設(shè)計思路和VHDL語言，實現(xiàn)對各個模塊單元的設(shè)計,、綜合和仿真,。為了簡化設(shè)計，只在數(shù)據(jù)輸入時鐘下輸入了一組64個復(fù)數(shù),，其余輸入設(shè)為0,，并且實部和虛部都限定在±l,，±2,，±3，±4,，e5之內(nèi),。為防止溢出先將輸入數(shù)據(jù)乘以一定比例因子2-9，再乘以2 15轉(zhuǎn)化為十六進(jìn)制數(shù),。輸出的結(jié)果如圖5所示,。需要注意的是：仿真結(jié)果乘以2 -6后才是實際結(jié)果。將仿真結(jié)果與Matlab計算的結(jié)果相比較,，數(shù)據(jù)基本一致,，說明了設(shè)計正確，其誤差主要來源于數(shù)據(jù)的截取和旋轉(zhuǎn)因子的近似,。

　　5 結(jié)束語

　　FFT算法是數(shù)字信號處理中一種重要運(yùn)算,，廣泛應(yīng)用于雷達(dá)、觀測,、跟蹤,、高速圖像處理、保密無線通信和數(shù)字通信等領(lǐng)域,。這里討論了一種基于FPGA的64點FFT處理器的設(shè)計方案,，輸入數(shù)據(jù)的實部和虛部均以16位二進(jìn)制數(shù)表示，采用基2DIT-FFT算法,，以Altera公司的QuartusⅡ軟件為開發(fā)平臺對處理器各個的模塊進(jìn)行設(shè)計,，在Stratix系列中的EP1S25型FPGA通過了綜合和仿真,，運(yùn)算結(jié)果正確。采用FPGA實現(xiàn)FFT算法在體積,、速度,、靈活性等方面都具有優(yōu)越性。