《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 測(cè)試測(cè)量 > 設(shè)計(jì)應(yīng)用 > 基于混沌同步的永磁同步電機(jī)控制
基于混沌同步的永磁同步電機(jī)控制
來源:電子技術(shù)應(yīng)用2010年第8期
岳永恒1,2,， 王 茂1,， 孫光輝1
1.哈爾濱工業(yè)大學(xué) 空間控制與慣性技術(shù)研究中心, 黑龍江 哈爾濱 150001;2. 東北林業(yè)大學(xué) 交通學(xué)院, 黑龍江 哈爾濱150040
摘要： 永磁同步電機(jī)的動(dòng)態(tài)特性與混沌Lorenz系統(tǒng)具有相似性,，一定的條件能夠使電機(jī)系統(tǒng)表現(xiàn)出類似hopf分岔的混沌特性,。針對(duì)永磁同步電機(jī)系統(tǒng),，分析了傳統(tǒng)PID控制器的缺點(diǎn),，并考慮到電機(jī)系統(tǒng)某些狀態(tài)變量不可測(cè)量的實(shí)際問題,，提出了一種基于混沌系統(tǒng)同步的非線性反饋控制器,，通過線性系統(tǒng)的零極點(diǎn)配置可以達(dá)到期望的響應(yīng)特性,。仿真結(jié)果驗(yàn)證了本控制器的有效性。
中圖分類號(hào)： TP273
文獻(xiàn)標(biāo)識(shí)碼： A
文章編號(hào)： 0258-7998(2010)08-0107-04
Permanent magnetism synchronous motor control based on chaos synchronization
YUE Yong Heng1,2, WANG Mao1,， SUN Guang Hui1
1. Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China;2. Traffic College, Northeast Forestry University, Harbin 150040, China
Abstract： The permanent magnetism synchronous motor (PMSM) performs the same dynamic behaviors as the Lorenz system. Special operating conditions leading to chaotic behavior and hopf bifurcation are presented and discussed, and the disadvantage of the traditional PID controller is analyzed. Considering the fact that some variables in practice can’t be directly measured, based on the synchronization of the chaotic system, a nonlinear feedback controller is designed. The designed controller exploits pole-placement approach to force the closed-loop system to have similar behavior as a simple linear system. The simulation results verify the effectiveness of the proposed controller in eliminating the chaotic oscillations.
Key words : chaos synchronization; permanent magnet synchronous motor; nonlinear feedback; lorenz system

    近年來,，隨著大功率電子器件的快速發(fā)展，永磁同步電機(jī)由于其高效性和良好的動(dòng)態(tài)特性,，在機(jī)器人,、航空航天領(lǐng)域都得到了廣泛的應(yīng)用[1]。但是由于其高速和弱磁區(qū)域控制受到較高的門限電壓限制[2],，大大限制了其應(yīng)用,。研究表明,，永磁同步電機(jī)系統(tǒng)像很多非線性系統(tǒng)一樣表現(xiàn)出多個(gè)穩(wěn)態(tài)工作點(diǎn)，在一定條件下,，可能出現(xiàn)極限環(huán)甚至混沌,。所以研究永磁同步電機(jī)系統(tǒng)在穩(wěn)態(tài)工作點(diǎn)附近的特性是近來研究的熱點(diǎn)。大量的文獻(xiàn)表明,，永磁同步電機(jī)在動(dòng)態(tài)特性上與混沌Lorenz系統(tǒng)具有相似性[3-5],。
　混沌系統(tǒng)是一種確定性系統(tǒng)，其運(yùn)動(dòng)軌跡敏感地依賴于系統(tǒng)的初始狀態(tài),，即兩個(gè)相同的混沌系統(tǒng)從非常接近的初始狀態(tài)出發(fā),，經(jīng)過一定的過渡時(shí)間之后，其運(yùn)動(dòng)軌跡將變得完全不同,。這和現(xiàn)實(shí)生活中的一些復(fù)雜系統(tǒng)所表現(xiàn)出來的特性非常相似,，即確定性系統(tǒng)所表現(xiàn)出的隨機(jī)性。系統(tǒng)的混沌特性在很多情況下是人們不希望的,，所以針對(duì)這些系統(tǒng),，研究了很多的控制方法來消除混沌現(xiàn)象。例如混沌的自適應(yīng)控制[6],、變結(jié)構(gòu)控制[7],、反饋控制等[8]。此外在混沌同步方面自從Pecora和Carroll的文章(即P-C同步法)[9]發(fā)表以來,，混沌同步的研究也取得了巨大的發(fā)展,。
　本文正是由混沌同步的觀點(diǎn)出發(fā)，設(shè)計(jì)出永磁同步電機(jī)的狀態(tài)觀測(cè)器,，從而構(gòu)造出非線性反饋控制器,，實(shí)現(xiàn)永磁同步電機(jī)的控制。通過簡單的線性系統(tǒng)的零極點(diǎn)配置方法,，便可以獲得期望的運(yùn)行特性,而且避免了PID校正中由于參數(shù)不當(dāng)而可能出現(xiàn)的混沌現(xiàn)象。
1 數(shù)學(xué)模型
　永磁同步電機(jī)的d-q模型廣泛地用于控制器設(shè)計(jì),。通過Park變換很容易將電機(jī)的交流變量轉(zhuǎn)換成直流變量,，極大地方便了控制系統(tǒng)設(shè)計(jì)。永磁同步電機(jī)的d-q模型可以表示為：


2 控制器設(shè)計(jì)
　　線性控制器尤其比例積分(PI)控制器在永磁同步電機(jī)速度控制中通常是首選的設(shè)計(jì)方案,。簡單地表述為雙閉環(huán)控制系統(tǒng)：內(nèi)環(huán)為電流環(huán),，外環(huán)為速度環(huán)。這里就以比例調(diào)節(jié)器為例,，說明傳統(tǒng)的線性調(diào)節(jié)器在永磁同步電機(jī)控制應(yīng)用中的弊端,。記Iqr和Idr分別為q軸和d軸的指令電流，而實(shí)際中Idr=0可以很容易得到保證[4],，則采用比例調(diào)節(jié)器的d-q電壓為: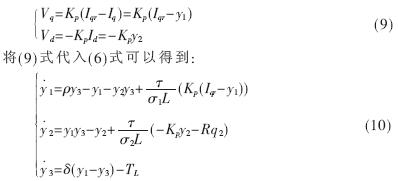

    為了得到不受驅(qū)動(dòng)的Lorenz系統(tǒng),可以使外部轉(zhuǎn)矩TL=0,，以及指令電流Iqr=0,。可以得到如下的模型:

將(7)式代入(11)式,，通過計(jì)算可以得到Lorenz系統(tǒng)族的Lyapunov指數(shù)集與反饋增益Kp的關(guān)系,，如圖2所示。圖中計(jì)算所采用的方法同樣是Wolf法,，只不過此時(shí)Lyapunov指數(shù)集的計(jì)算與反饋增益Kp息息相關(guān),。
    從圖2可以看出永磁同步電機(jī)在較小的反饋增益 Kp(Kp<86)下能夠保持穩(wěn)定，隨著Kp的增加,，混沌化逐漸加劇,。在控制系統(tǒng)設(shè)計(jì)時(shí)，一方面為了保證系統(tǒng)的響應(yīng)速度,，必須有較大的反饋增益,；而另一方面，大的反饋增益又容易使系統(tǒng)混沌化,。對(duì)于PI調(diào)節(jié)器,，也有同樣的結(jié)果。受非線性反饋的啟發(fā)[14],，可以引入如下的反饋:

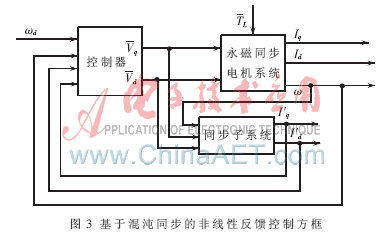
　　通過簡單的零極點(diǎn)配置方法,，閉環(huán)系統(tǒng)就能得到期望的性能。更進(jìn)一步來說,，實(shí)際系統(tǒng)中某些變量是不能直接測(cè)量的,，例如現(xiàn)在研究的同步電機(jī)無位置傳感器控制就是只能測(cè)量電機(jī)的角速度?棕。為此,，可以構(gòu)造基于混沌同步的狀態(tài)觀測(cè)器,，估計(jì)出其他變量，從而可以實(shí)現(xiàn)控制,。其結(jié)構(gòu)框圖如圖3所示,。也就是說，通過構(gòu)造與永磁同步電機(jī)相關(guān)的同步子系統(tǒng),，將控制所需的電機(jī)狀態(tài)變量用通過同步后的子系統(tǒng)變量代替,，從而形成閉環(huán)控制。

  　　本文首先介紹了永磁同步電機(jī)與混沌Lorenz系統(tǒng)在數(shù)學(xué)模型上的相似之處,。永磁同步電機(jī)本身是不會(huì)呈現(xiàn)混沌特性的,，但是隨著電機(jī)外部力矩的變化及q軸電壓的變化，就有可能產(chǎn)生混沌現(xiàn)象,。傳統(tǒng)的PI控制器在抑制混沌上作用又不是很明顯,。由此引入了非線性反饋控制，該控制器能夠使非線性的電機(jī)系統(tǒng)轉(zhuǎn)化為普通的一階系統(tǒng),，從而可以通過線性系統(tǒng)的零極點(diǎn)配置達(dá)到期望的響應(yīng)特性,?？紤]到實(shí)際系統(tǒng)的某些變量可能無法測(cè)量，在非線性反饋的基礎(chǔ)之上,，引入了基于混沌降階同步的狀態(tài)觀測(cè)器,，用估計(jì)值代替某些不可測(cè)量的變量，進(jìn)而構(gòu)成非線性反饋,，實(shí)現(xiàn)了電機(jī)系統(tǒng)的控制,。同時(shí)通過Lyapunov直接法證明了觀測(cè)器的穩(wěn)定性。仿真結(jié)果也證明了該控制器的有效性,。
參考文獻(xiàn)
[1]  王立欣, 王宇野, 王豐欣. 基于DSP的電動(dòng)車用永磁同步電機(jī)的控制方法[J]. 電機(jī)與控制學(xué)報(bào), 2005,9(1): 51-54.
[2]  JAHNS T M, KLINMAN G B, NEUMANN T W. Interior permanent magnet synchronous motors for adjustable-speed    drives[J]. IEEE Transactions on Industrial Applications, 1986,22(4):738-747.
[3]  HEMATI N, KWATNY H. Bifurcation of equilibria and  chaos in permanent-magnet machines[C]. Proceedings of  the 32nd conference on Decision and control, December 1993:425-429.
[4]  楊志紅, 姚瓊薈. 無刷直流電動(dòng)機(jī)系統(tǒng)非線性研究[J].動(dòng)力學(xué)與控制學(xué)報(bào), 2006,4(1):59-62.
[5]  HEMATI N.  Strange attractors in brushless DC motors. IEEE Transactions on Circuits and Systems-I:Fundamental Theory and Application. 1994,41(1):40-45.
[6]  LI Shuang, XU Wei, LI Rui Hong. Synchronization of two     different chaotic systems with unknown parameters[J].Phys.     Lett. A, 2007,361(1):98-102.
[7]  LI Xiao Run, ZHAO Liao Ying, ZHAO Guang Zhou.  Sliding mode controlfor synchronization of chaotic systems with structure or parameters mismatching[J]. Zhejiang Univ    SCI, 2005(6):571-576.
[8]  HUANG L L,WANG M, FENG R. Parameters identification and adaptive synchronization of chaotic systems with  unknown parameters[J]. Phys. Lett. A, 2005,342:299-304.
[9]  PECORA L M, CARROLL T M.Synchronization of chaotic systems[J]. Phys Rev Lett, 1990,64(8):821-830.
[10]  HEMATI N, LEU M C. A complete model characterization of brushless DC motors[J]. IEEE Transactions on  Industry Applications. 1992,28(1):172-180.
[11]  GE Zheng Ming, CHANG Ching Ming, CHEN Yen Sheng. Anti-control of chaos of single time scale brushless dc motors and chaos synchronization of different order systems[J]. Chaos, Solitons and Fractals, 2006,27:1298-1315.
[12]  JING Zhu Jun, CHANG Yu, CHEN Guan Rong. Complex dynamics in a permanent-magnet synchronous motor model[J]. Chaos, Solitons and Fractals, 2004,22:831-848.
[13]  GE Z M, CHENG J W. Chaos synchronization and parameter identification of three time scales brushless DC motor system[J]. Chaos, Solitons and Fractals, 2005, 24:597-616.
[14]  ZAHER A A. A nonlinear controller design for permanent magnet motors using a synchronization-based technique inspired from the Lorenz system[J]. CHAOS, 2008,18:(1).

此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載。