金屬氧化物半導(dǎo)體場效應(yīng)晶體管(Metal-Oxide-Semiconductor Field-Effect Transistor,，MOSFET)是由一個(gè)金氧半(MOS)二機(jī)體和兩個(gè)與其緊密鄰接的P-n接面(p-n junction)所組成,。自從在1960年首次證明后，MOSFET快速的發(fā)展,，并且成為微處理器與半導(dǎo)體記憶體(memory)等先進(jìn)集成電路中最重要的元件,。隨著超大型集成電路(VLSI)的快速發(fā)展，淺溝槽隔離(STI)技術(shù)在MOSFET制成中得到了廣泛的應(yīng)用,。當(dāng)MOSFET的有效通道長度(L)和寬度(W)的尺寸越來越小時(shí),，一種MOS器件的失效模式：雙峰效應(yīng)(double-hump)也越來越受到人們的重視,。

　　1 雙峰效應(yīng)

　　圖1是典型的雙峰效應(yīng)示意圖,。在圖中虛線方框中,，電流Id在閥極電壓Vg很小的時(shí)候出現(xiàn)了一個(gè)峰值,。在整個(gè)Id-Vg曲線中出現(xiàn)兩個(gè)峰值，稱之為雙峰效應(yīng),。它的表現(xiàn)是在次臨界區(qū)(sub-threshold)，MOS還沒有開啟時(shí)(Vg

　　圖1中，NMOS的W和L分別為10μm和0.18μm;Vsource=0;Vdrain=0.1 V;Vsub=0,，-0.45 V，-0.9 V,，-1.35 V,，-1.8 V;Vg從0升到1.8 V。近幾年,，人們對(duì)這種失效現(xiàn)象做了大量的研究,。人們普遍接受，晶體管的側(cè)壁寄生晶體管的預(yù)先開啟是漏電的根本原因,。理論上講,，由于粒子注入的有效摻雜濃度在晶體管的中心區(qū)域和側(cè)壁位置的不同，導(dǎo)致了側(cè)壁寄生晶體管的預(yù)先開啟,。在MOS的基板加有反向電壓時(shí),，雙峰現(xiàn)象特別明顯。圖2中TrenchrecesS和Corner out-doping這兩種現(xiàn)象可以被用來解釋為什么晶體管的側(cè)壁位置粒子注入的摻雜濃度會(huì)不同于晶體管中心位置(通道正下方),。由于Trenchrecess和Corner ou-doping這兩種現(xiàn)象是不可避免的,，所以人們嘗試了很多種方法去優(yōu)化摻雜的有效濃度分布，以期降低和消除雙峰效應(yīng),。

　　本文將介紹一種雙峰效應(yīng)的簡單評(píng)估方法,，使雙峰效應(yīng)的程度得以量化。并且通過對(duì)量化數(shù)字的評(píng)估，可以定性和定量地了解和確定最優(yōu)化的摻雜濃度條件,。

　　2 實(shí)驗(yàn)條件

　　本文分別對(duì)N型MOS的Vt和Punch-through的粒子注入摻雜濃度進(jìn)行了正交試驗(yàn),。其中，Vt注入的濃度分別為：4.55×1012cm-2;6.55×1012cm-2和8.55×1012cm-12,。,，注入能量為25 kev，雜質(zhì)成分為硼(Boron);Punch-through注入的濃度分別為：4.0×1012cm-2;7.13×1012cm-2和1.0×1013cm-2,，注入能量為170 kev,，雜質(zhì)成分為銦(Indium);通過對(duì)不同注入條件的MOS器件的Jd-Vg曲線的測量和分析，以期能得到摻雜濃度分布和雙峰效應(yīng)的關(guān)系,。

　　3 雙峰效應(yīng)的評(píng)估方法

　　圖3(a)是N型MOS器件的Id-Vg測量曲線,。MOS器件的W和L分別為10 μm和0.18μm，測量條件為：Vsource=O;Vdrain=0.1V;Vsub=-1.8 V;Vg從0升到1.8 V;圖中實(shí)線表示Id的測量值,，可以看到很明顯的雙峰現(xiàn)象,。由于Vg很小的區(qū)間，測試電流值很小,，而且不準(zhǔn)確,，所以取Vg在O.5～1.OV這個(gè)區(qū)間作為雙峰效應(yīng)的評(píng)估區(qū)間。圖3(b)中的虛線為理想的Id-Vg曲線,?？梢愿鶕?jù)MOS在(Vg比較高)線性區(qū)和飽和區(qū)的測量值，采用多項(xiàng)式近似曲線擬合法(Polynomi-al Regression Fitting)反向推導(dǎo)得出,。圖中實(shí)線測量值和虛線擬合值的陰影部分表明了MoS器件的漏電程度,，用陰影面積來作為雙峰效應(yīng)的量化評(píng)估值。

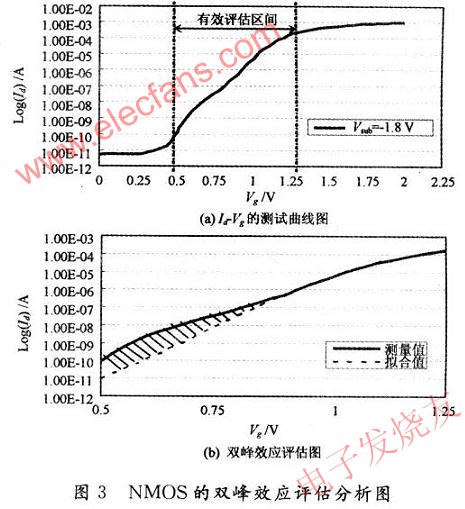
　　4 試驗(yàn)分析

　　通過對(duì)各種實(shí)驗(yàn)條件的Id-Vg曲線的測量和雙峰效應(yīng)的評(píng)估,，以粒子注入的濃度變化作為變量,，雙峰效應(yīng)的量化值作為結(jié)果，建立了兩者變化關(guān)系的模型,。圖4和圖5分別是模型的精確度評(píng)估圖和注入濃度對(duì)雙峰效應(yīng)的變化模型圖,。

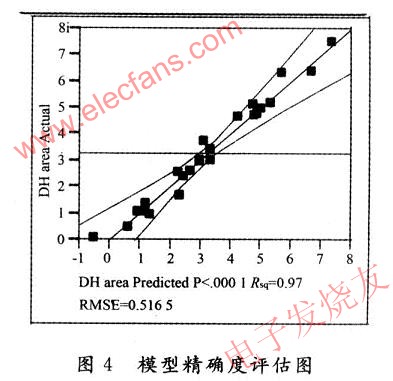
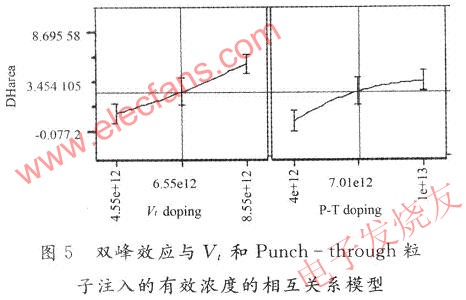
　　從圖4可以看出模型的精確度(Rsquare)為O.97。這表明,，粒子注入濃度和雙峰效應(yīng)具有非常強(qiáng)的相關(guān)性,。圖5顯示，雙峰效應(yīng)對(duì)Vt的注入濃度非常敏感,。隨著濃度的上升,，雙峰效應(yīng)越來越明顯。這個(gè)現(xiàn)象和現(xiàn)有的理論相吻合,。由于Vt的注入能量為25 kev,，有效摻雜濃度的峰值靠近MOS通道的表面,。并且硼的吸出效應(yīng)(out-doping)明顯，隨著粒子注入濃度的升高,，通道正下方的有效摻雜濃度上升,，但側(cè)壁位置的有效濃度變化不大，致使這兩個(gè)位置的濃度差異增加,。同時(shí),，硼的有效濃度的增加，會(huì)導(dǎo)致通道正下方的閾值臨界電壓Vt的上升,。這個(gè)變化會(huì)使得MOS通道下方開啟時(shí)間延遲,，從而側(cè)壁寄生晶體管的預(yù)先開啟時(shí)間變長，進(jìn)一步導(dǎo)致漏電量的增加,。同理,，采用的雙峰效應(yīng)的量化評(píng)估值就會(huì)增加，雙峰效應(yīng)明顯,。與Vt注入相比,，Punch-through注入的濃度變化對(duì)雙峰效應(yīng)的影響不明顯。這是因?yàn)殂熢氐奈鲂?yīng)不明顯,，所以銦的有效濃度的變化對(duì)通道正下方和側(cè)壁位置的有效摻雜濃度的差異貢獻(xiàn)不大,，從而雙峰效應(yīng)對(duì)銦的濃度變化相對(duì)不敏感。

　　本文的模型可以用于定性和定量的分析,，但是對(duì)于MOSFET來說,，V的粒子注入條件也影響晶體管整體的電學(xué)特性。所以,，在確定最優(yōu)化的摻雜濃度條件時(shí),，要綜合考慮,。

　　5 結(jié) 語

　　MOSFET的中心區(qū)域和側(cè)壁位置的有效摻雜粒子濃度的均勻分布是解決雙峰效應(yīng)的根本條件,。不論這兩個(gè)位置的有效摻雜濃度差異的形成原因，理論上都可以找到一個(gè)比較優(yōu)化的工藝條件,，使得有效摻雜濃度分布均勻,，從而減少或消除雙峰效應(yīng)的影響。通過對(duì)雙峰效應(yīng)的量化評(píng)估,，建立摻雜濃度和雙峰效應(yīng)相互關(guān)系的模型,，從定性和定量的角度進(jìn)一步了解和確定優(yōu)化條件。