摘   要： 在分析已有算法的基礎(chǔ)上,，利用增量法與分治法相結(jié)合的思想,實(shí)現(xiàn)了直接對空間散亂點(diǎn)的三角剖分,。通過對空間散亂點(diǎn)的三角剖分，最終得到滿足所要重建物體的三角網(wǎng)格模型,，且網(wǎng)格非常均勻,該模型直觀,、清晰地再現(xiàn)了實(shí)體模型,。實(shí)驗(yàn)證明了算法的可行性。
關(guān)鍵詞： 三維重建; 空間散亂點(diǎn); 三角剖分; 增量法; 分治法

    在計(jì)算機(jī)視覺中,三維重建是指由多幅二維圖像恢復(fù)物體三維可見表面幾何形狀的方法（物體的空間位置信息）,。三維重建直接模擬人類雙眼處理景物的方式,，具有簡單、可靠,、靈活,、使用范圍廣等特點(diǎn)，可以進(jìn)行非接觸,、自動(dòng),、在線檢測等。
　從某種角度上說,，三維重建的最終目的是可視,，就是把被重建的物體真實(shí)地顯示出來。由三維重建算法得到的是一組三維點(diǎn)集,，并不能求得整個(gè)物體表面的細(xì)節(jié),，因此需要對這些散亂的三維點(diǎn)進(jìn)行三角剖分，用許多小三角形組成的表面來近似物體表面,，這樣就相當(dāng)于給散亂的三維點(diǎn)集搭起一個(gè)立體的網(wǎng)狀骨架模型,。經(jīng)過三角剖分之后，所有三角形的平面片在空間撐出了物體的三維模型,。這時(shí)只需要將物體的紋理從圖像中取出,，并映射至三維模型上就可以提供物體的真實(shí)三維模型。
　三角剖分是虛擬現(xiàn)實(shí),、計(jì)算機(jī)視覺等領(lǐng)域的一個(gè)研究熱點(diǎn),。目前針對三角化的研究主要有：BOLL和VEMURI[1]、 BRINKLEY和SCHMITT等采用參數(shù)表示法,，將三維數(shù)據(jù)映射到二維參數(shù)域上,在二維進(jìn)行曲面重構(gòu),然后將結(jié)果映射回三維空間,；BOWYER和WATSON[2]采用Delaunay三角剖分法,將二維的Delaunay三角剖分推廣到三維進(jìn)行網(wǎng)絡(luò)重構(gòu)。BERNARIDINI 的 BPA 算法[3]通過種子三角形不斷向周圍擴(kuò)展,，從而構(gòu)成最終的三角形網(wǎng)格等,。
　目前,對于平面區(qū)域的散亂點(diǎn)集三角剖分已經(jīng)取得了一定的成果，但很多算法推廣至三維空間仍存在一些問題,，在算法的時(shí)間效率上也有待進(jìn)一步提高,，因此對于三維空間散亂點(diǎn)集的三角剖分有待進(jìn)一步的發(fā)展。
　本文提出了一種利用增量法與分治法相結(jié)合的算法,，直接對空間散亂點(diǎn)進(jìn)行三角剖分,，降低算法的時(shí)間復(fù)雜度，并通過編程證明了該算法的可行性,。
1  三角剖分算法的基礎(chǔ)理論
　三角剖分中以Delaunay三角剖分最具有代表性,，它是優(yōu)化的三角剖分,。Delaunay三角剖分的概念是1934年由俄國數(shù)學(xué)家Delaunay提出的。  
   三角剖分所具備的優(yōu)異特性主要有以下幾個(gè)方面：
   (1)最接近：以最臨近的三點(diǎn)形成三角形,，且各線段(三角形的邊)皆不相交,；
   (2)唯一性：不論從區(qū)域何處開始構(gòu)建，最終都將得到一致的結(jié)果,；
　(3)最優(yōu)性：任意兩個(gè)相鄰三角形形成的凸四邊形的對角線如果可以互換的話,，那么兩個(gè)三角形6個(gè)內(nèi)角中最小的角度不會(huì)變大；
　(4)最規(guī)則：如果將三角網(wǎng)中的每個(gè)三角形的最小角進(jìn)行升序排列,，則Delaunay三角網(wǎng)的排列得到的數(shù)值最大,；
　(5)區(qū)域性：新增、刪除,、移動(dòng)某一個(gè)頂點(diǎn)時(shí)只會(huì)影響臨近的三角形,；
　(6)具有凸多邊形的外殼：三角網(wǎng)最外層的邊界形成一個(gè)凸多邊形的外殼。
　關(guān)于Delaunay三角剖分主要有三類:增量算法(逐點(diǎn)插入法),、分治法(分割歸并算法)和三角網(wǎng)生長算法,。三角網(wǎng)生長法在20世紀(jì)80年代中期以后就很少用到,較常見的是分治算法和逐點(diǎn)插入法。
　增量算法的思想：先構(gòu)造一個(gè)包含所有點(diǎn)集的大三角形,，然后逐點(diǎn)在三角形內(nèi)插入點(diǎn),，插入的過程不斷用Delaunay三角優(yōu)化準(zhǔn)則去檢查和調(diào)整，直到所有點(diǎn)插入完整,，算法結(jié)束,。
　逐點(diǎn)插入法有不同的實(shí)現(xiàn)方法，區(qū)別在于初始多邊形的不同和初始三角剖分的方法不同,。較有代表性的是Lawson算法[4]以及Lee和Schacher算法[5],。
   分治算法的思想：所謂的分治法，其實(shí)就是分而治之,。首先把要處理的點(diǎn)集分成幾個(gè)相等的子點(diǎn)集，按Delaunay三角優(yōu)化準(zhǔn)則對各子點(diǎn)集進(jìn)行三角剖分,，然后把各個(gè)子集的相鄰三角形邊界進(jìn)行合并,，最后對合并時(shí)在子集邊界處新生成的三角形進(jìn)行優(yōu)化。
   分治法也有不同的實(shí)現(xiàn)方法,其不同之處在于使用不同的子集劃分方法,、子集中三角剖分方法或者各子集邊界的合并方法,，比較經(jīng)典的算法是Lee和Schacher算法[5]、Dwyer算法[6],。
2 改進(jìn)的三角剖分算法
2.1 復(fù)雜度及優(yōu)缺點(diǎn)分析
　增量算法簡單直觀,，占用內(nèi)存小，魯棒性好,，容易實(shí)現(xiàn),，但時(shí)間復(fù)雜度差,最壞情況為O(n2),。當(dāng)處理的散亂點(diǎn)數(shù)量增長時(shí)，處理的時(shí)間也指數(shù)地增長,，故降低其時(shí)間復(fù)雜度顯得相當(dāng)重要,。
　分治算法時(shí)間復(fù)雜度方面較好，其最壞情況為O(lgn),，但由于遞歸執(zhí)行,，需要較大的內(nèi)存空間，對于大規(guī)模的散亂點(diǎn)的處理要求大量的內(nèi)存空間,。
　兩種算法各有自己的優(yōu)點(diǎn)和缺點(diǎn),，增量算法時(shí)間效率差，節(jié)省內(nèi)存空間;而分治法時(shí)間效率好,，但需要大量內(nèi)存,。          
　改進(jìn)的算法思想是把分治算法與增量法結(jié)相結(jié)合，以分治算法為主體,增量法為輔：當(dāng)遞歸分割數(shù)據(jù)點(diǎn)集的過程進(jìn)行到子點(diǎn)集中的數(shù)據(jù)量小于一個(gè)預(yù)定值——分割閾值時(shí)終止,然后用增量法在子集中生成子三角網(wǎng),。這一新的算法稱為合成算法,。
2.2 算法的改進(jìn)
2.2.1 分治法中的改進(jìn)
   分治法中采用一對八式的八叉樹數(shù)據(jù)模型來完成分割與合并。
　首先利用八叉樹模型對空間離散點(diǎn)進(jìn)行分割,，然后對八叉樹葉子節(jié)點(diǎn)進(jìn)行Delaunay三角化,，最后依據(jù)Delaunay法則將各局部三角網(wǎng)自下而上逐級合并，進(jìn)而生成最終的整個(gè)點(diǎn)集三角網(wǎng)模型,這樣將兩種三角化適當(dāng)結(jié)合,，提高了算法的效率,。
　其中，在合并的過程中盡量減少了查找正確擴(kuò)展點(diǎn)的范圍,，從而節(jié)約了時(shí)間,，提高了算法的執(zhí)行效率。
　具體作法：將各節(jié)點(diǎn)生成三角網(wǎng)凸殼的擴(kuò)展邊（邊界）找出,，用鏈表分別存儲(chǔ),，兩兩合并三角網(wǎng)時(shí)所需用到的邊和點(diǎn)就可直接取自這兩條鏈表中的數(shù)據(jù)，而無需在該區(qū)域中所有點(diǎn)中逐一比較尋找了,，從而避免了很多無用功,。
    用八叉樹來表示三維形體，既可以看成是四叉樹方法在三維空間的推廣,，也可以認(rèn)為是用三維體素陣列表示形體方法的一種改進(jìn),如圖1所示,。

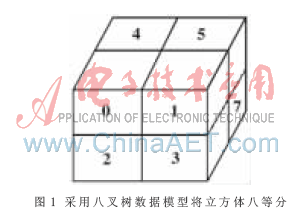
    八叉樹有三種不同的存儲(chǔ)結(jié)構(gòu)，分別是規(guī)則方式,、線性方式以及一對八方式,。相應(yīng)的八叉樹也分別稱為規(guī)則八叉樹、線性八叉樹以及一對八式八叉樹,。不同的存儲(chǔ)結(jié)構(gòu)的空間利用率及運(yùn)算操作的方便性是不同的,。分析表明,，一對八式八叉樹優(yōu)點(diǎn)更多一些。
    (1)規(guī)則八叉樹
     規(guī)則八叉樹缺陷較多,，最大的問題是指針占用了大量的空間,。假定每個(gè)指針要用2 B表示，而節(jié)點(diǎn)的描述用1 B,則存放指針要占總存儲(chǔ)量的94％,。因此,，這種方法雖然十分自然，容易掌握,，但在存儲(chǔ)空間的使用率方面不是很理想,。
    (2)線性八叉樹
    線性八叉樹不僅節(jié)省存儲(chǔ)空間，對某些運(yùn)算也較為方便,但是為此付出的代價(jià)是喪失了一定的靈活性,。
    (3)一對八式的八叉樹
     一個(gè)非葉節(jié)點(diǎn)有8個(gè)子節(jié)點(diǎn),，為了確定起見，將它們分別標(biāo)記為0,、1,、2、3,、4,、5、6,、7,。綜上所述，如果一個(gè)記錄與一個(gè)節(jié)點(diǎn)相對應(yīng),，那么在這個(gè)記錄中描述的是這個(gè)結(jié)點(diǎn)的8個(gè)子節(jié)點(diǎn)的特性值,。而指針給出的則是該8個(gè)子節(jié)點(diǎn)所對應(yīng)記錄的存放處，而且還隱含地假定了這些子結(jié)點(diǎn)記錄存放的次序,。也就是說,，即使某個(gè)記錄是不必要的(例如該節(jié)點(diǎn)已是葉節(jié)點(diǎn))，則相應(yīng)的存儲(chǔ)位置也必須空閑在那里,，以保證不會(huì)錯(cuò)誤地存取到其他同輩節(jié)點(diǎn)的記錄,。這樣當(dāng)然會(huì)有一定的浪費(fèi)，除非它是完全的八叉樹,，即所有的葉節(jié)點(diǎn)均在同一層次出現(xiàn)，而在該層次之上的所有層中的節(jié)點(diǎn)均為非葉節(jié)點(diǎn),。
    綜上優(yōu)缺分析后,，文中選擇了一對八式的八叉樹數(shù)據(jù)模型。
2.2.2 Delaunay增量算法的改進(jìn)
    Delaunay增量算法的思想是逐點(diǎn)插入,每次插入一個(gè)散亂點(diǎn),，經(jīng)處理形成若干新的四面體;但隨著插入點(diǎn)的增加,，所生成的四面體便成倍地增長,，而計(jì)算量也大大增加。
    如何縮短算法中各個(gè)環(huán)節(jié)的計(jì)算時(shí)間成為提高整個(gè)算法效率的關(guān)鍵,。這些關(guān)鍵問題涉及散亂點(diǎn)的加入方式,、搜索方法等。
    本文在搜索四面的外接圓時(shí)使用了指南針?biāo)惴?，提高了算法的搜索效率?br /> 2.3 可行性分析
    (1)采用八叉樹分割,，并用遞歸的思想，當(dāng)數(shù)據(jù)量大的時(shí)候,，調(diào)用的程序運(yùn)行效率比較低,。在本程序的實(shí)現(xiàn)中，將遞歸調(diào)用轉(zhuǎn)化為迭代,，從而提高算法效率[7,8],。
    (2)文中在增量算法中嵌入了指南針?biāo)惴ㄋ褜に拿骟w外接球體，以加快算法的搜尋速度,。
    (3)在合并的過程中盡量縮小查找正確擴(kuò)展點(diǎn)的范圍,提高了算法的執(zhí)行效率,。
3 實(shí)驗(yàn)
    本文的實(shí)驗(yàn)環(huán)境：CPU為Pentium(R) Dual-Core 2.5 GHz，內(nèi)存1 GB,，顯卡為集成顯卡,，操作系統(tǒng)為Window XP，仿真平臺(tái)為Matlab 7.0,。
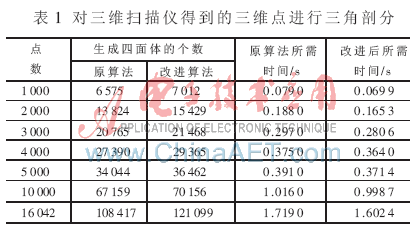
    (1)選取通過三維掃描儀得到的點(diǎn)云圖,，分別利用Matlab中的Delaunay（）函數(shù)剖分和改進(jìn)的三角剖分算法對點(diǎn)云圖進(jìn)行剖分，在點(diǎn)數(shù)變化時(shí),，對兩種算法所剖分出四面的數(shù)量和所用時(shí)間進(jìn)行比較,結(jié)果如表1所示,。

    (2)選取通過三維掃描儀得到的一條圍巾的點(diǎn)云圖，分別利用Matlab中Delaunay( )函數(shù),、Delaunayn( )剖分和改進(jìn)的三角剖分算法對點(diǎn)云圖進(jìn)行剖分,。通過三維掃描儀掃描圍巾得到點(diǎn)云,如圖2所示，使用原算法和改進(jìn)算法對圍巾點(diǎn)云圖進(jìn)行三角剖分,，結(jié)果如圖3和圖4所示,。

　 對圖3和圖4中的1號與2號區(qū)域放大,比較效果分別如圖5、圖6,、圖7,、圖8所示。

    使用兩種算法對圍巾點(diǎn)云剖分在剖分出四面的數(shù)量和所用時(shí)間方面進(jìn)行比較,結(jié)果如表2所示,。

    通過對不同數(shù)量的空間散亂點(diǎn)的三角剖分,，利用Matlab內(nèi)置的Delauany()函數(shù)與改進(jìn)的三角剖分算法對空間散亂點(diǎn)集進(jìn)行三角剖分，對剖分出四面體的數(shù)量和所用時(shí)間進(jìn)行比較，改進(jìn)的算法在剖分出的四面體數(shù)量和時(shí)間效率上有明顯的優(yōu)勢,。而且由以上圖的比較可以看出,，對于重建出的模型效果，改進(jìn)后的算法明顯優(yōu)于前者,。
    本文算法通過使用分治法和增量法的合成算法,，在分治法中使用八叉樹數(shù)據(jù)模型，使遞歸問題轉(zhuǎn)化為迭代問題,，提高了算法的執(zhí)行效率,；在增量法中嵌入指南針?biāo)惴ǎ岣吡怂阉餍?。使用合成算法在空間的三角剖分方面有很大的優(yōu)勢,。此外分析了算法中的不足之處，并提出有待進(jìn)一步研究的問題,，為后續(xù)的展望工作打下基礎(chǔ),。
參考文獻(xiàn)
[1]  BOLLE R M,    VEMURI B C. On three-dimensional surface reconstruction methods. IEEE Trans.Pat.Anal.Mach.Intell, 1985,7(4):431-441.
[2]  WATSON D F. Computing the N-dimensional delaunay  tessellation with application to voronoi polytopes.The Computer Journal,1981,24(2):167-172.
[3]  BERARIDINI F, MITTLEMAN J, SILVA C, et al. The ball-pivoting algorithm for surface reconstruction. IEEE  Trans.Virsualization Comput. Graphics, 1999(4):43-72.
[4]  LAWSON G L. Generation of a triangular grid with application to contour plotting[C]. In:Teehnical Memorandum.  Institute of Technology, Jet Pollution Laboratory,California,1972:294-299.
[5]  LEE D T, SCHACHER B J. Two algorithms for eonstrueting a delaunay triangulation[J]. International Journal of  Computer and Information Seienees,1980(9):219-242.
[6]  DWYER R A. A faster divide-and-conquer algorithm fore constructing Delaunay triangulations [J]. Algorithmica, 1987(2):137-151.
[7]  朱站立，劉天時(shí).數(shù)據(jù)結(jié)構(gòu)（第二版）[M].西安：西安交通大學(xué)出版社,，1999.
[8]  PIEGL L A, RICHARD A M. Algorithm and data structure for triangulating multiply connected polyonal domains [J].Computers & Graphics,1993,14(16);23-35.