直接轉(zhuǎn)矩控制(DTC)交流調(diào)速技術(shù)是繼矢量控制變頻之后發(fā)展起來(lái)的一種新型的具有高性能的變頻調(diào)速技術(shù),。DTC借助瞬時(shí)空間矢量理論在定子靜止坐標(biāo)系下計(jì)算電動(dòng)機(jī)的磁鏈和轉(zhuǎn)矩，通過(guò)轉(zhuǎn)矩兩點(diǎn)式調(diào)節(jié)器把轉(zhuǎn)矩檢測(cè)值與給定值做滯環(huán)的比較,，把轉(zhuǎn)矩波動(dòng)限制在一定的容差范圍內(nèi),，其控制效果取決于轉(zhuǎn)矩的實(shí)際狀況，具有結(jié)構(gòu)簡(jiǎn)單和動(dòng)態(tài)響應(yīng)快的優(yōu)點(diǎn),。
異步電機(jī)的狀態(tài)方程是一組非線性方程,，根據(jù)系統(tǒng)辨識(shí)理論，對(duì)非線性系統(tǒng)" title="非線性系統(tǒng)">非線性系統(tǒng)狀態(tài)估計(jì)的最好方法是擴(kuò)展卡爾曼濾波" title="卡爾曼濾波">卡爾曼濾波。本文以定子電流和轉(zhuǎn)子磁鏈為狀態(tài)變量,，將角速度作為估算的參數(shù),，利用擴(kuò)展卡爾曼濾波(EKF)方法估算異步電機(jī)的角速度和轉(zhuǎn)子磁鏈，由此建立異步電機(jī)無(wú)速度直接轉(zhuǎn)矩控制系統(tǒng),。
1 擴(kuò)展卡爾曼濾波器
卡爾曼濾波是60年代發(fā)展起來(lái)的一種現(xiàn)代濾波方法,，它的一個(gè)重要作用在于系統(tǒng)的狀態(tài)估計(jì)。當(dāng)噪聲是正態(tài)分布情況時(shí),，這種濾波給出了狀態(tài)的最小方差估計(jì),，當(dāng)不是正態(tài)分布情況時(shí)，這種濾波給出了狀態(tài)的線性最小方差估計(jì),?？柭鼮V波算法是一種應(yīng)用于線性系統(tǒng)中的迭代估計(jì)算法，為了能夠在非線性的感應(yīng)電機(jī)模型中應(yīng)用卡爾曼濾波算法,，首先需要將非線性系統(tǒng)線性化" title="線性化">線性化,。通過(guò)對(duì)非線性函數(shù)" title="非線性函數(shù)">非線性函數(shù)的Talor展開(kāi)式進(jìn)行一階線性化截?cái)啵瑥亩鴮⒎蔷€性問(wèn)題轉(zhuǎn)化為線性問(wèn)題,。
一般非線性系統(tǒng)模型為：
式中,，W(t)和V(t)分別稱(chēng)為系統(tǒng)噪聲矩陣和測(cè)量噪聲矩陣。測(cè)量噪聲矩陣由測(cè)量的不準(zhǔn)確性造成,，一般W(t)和V(t)都被假設(shè)為零均值的高斯白噪聲,，其方差矩陣分別為Q和R。
對(duì)上式的離散隨機(jī)非線性系統(tǒng),，可以寫(xiě)為
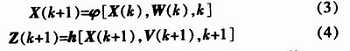
式中,，ψ[]為n維向量非線性函數(shù)；h[]為m維向量非線性函數(shù),。
將離散隨機(jī)非線性系統(tǒng)狀態(tài)方程式中的非線性向量函數(shù)ψ[]圍繞濾波值
展開(kāi)成泰勒級(jí)數(shù),，并略去二次以上項(xiàng)，得：
這樣,，非線性系統(tǒng)的狀態(tài)估計(jì)問(wèn)題就轉(zhuǎn)化為線性系統(tǒng)的狀態(tài)估計(jì)問(wèn)題了,，按照卡爾曼濾波的推演方法，得到EKF算法步驟如下：
EKF算法在電機(jī)狀態(tài)估計(jì)中的應(yīng)用如圖1所示,。
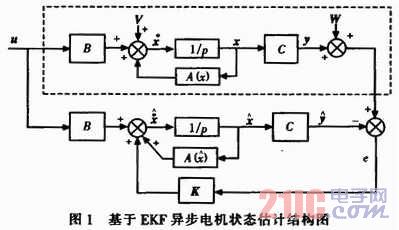
圖1上半部分的虛框內(nèi)表示的是電動(dòng)機(jī)實(shí)際狀態(tài),，下半部分是EKF狀態(tài)估計(jì)框圖，符號(hào)“＾”表示狀態(tài)矢量估計(jì),，K為EKF增益矩陣,。
2 利用EKF進(jìn)行轉(zhuǎn)子轉(zhuǎn)速估計(jì)
異步電機(jī)在兩相靜止α、β坐標(biāo)下的數(shù)學(xué)模型：
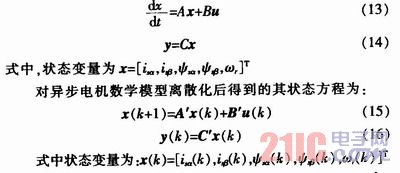
這樣就得到了離散化及線性化處理后的適合進(jìn)行卡爾曼濾波運(yùn)算的函數(shù)表達(dá)式,，可以代入EKF算法進(jìn)行迭代運(yùn)算,。
3 EKF建模與DTC系統(tǒng)仿真
本文的仿真和建模是在Matlab7．O的Simulink環(huán)境下完成的,，主要包括異步電動(dòng)機(jī)模型、轉(zhuǎn)矩調(diào)節(jié)器,、磁鏈調(diào)節(jié)器,、磁鏈自控制、開(kāi)關(guān)信號(hào)選擇單元,，其中擴(kuò)展卡爾曼濾波模塊是由S函數(shù)編寫(xiě),。
感應(yīng)電機(jī)參數(shù)如下：定子自感Ls=0．610 8 H，轉(zhuǎn)子自感Lr=0．607 9 H,，定,、轉(zhuǎn)子互感Lm=0．593 2 H，定子相繞組電阻Rs=3．67 Ω,，轉(zhuǎn)子相繞組電阻Rr=2．613 Ω,，轉(zhuǎn)動(dòng)慣量J=0．027 5kg·m2，極對(duì)數(shù)p=2,。
為驗(yàn)證該系統(tǒng)的精,、動(dòng)態(tài)性能，系統(tǒng)空載啟動(dòng),，設(shè)定轉(zhuǎn)速為100 rad／s,，進(jìn)入穩(wěn)定后，在t=0．5 s時(shí)加入負(fù)載TL=5 N·m,，仿真圖如圖2～圖5所示,。
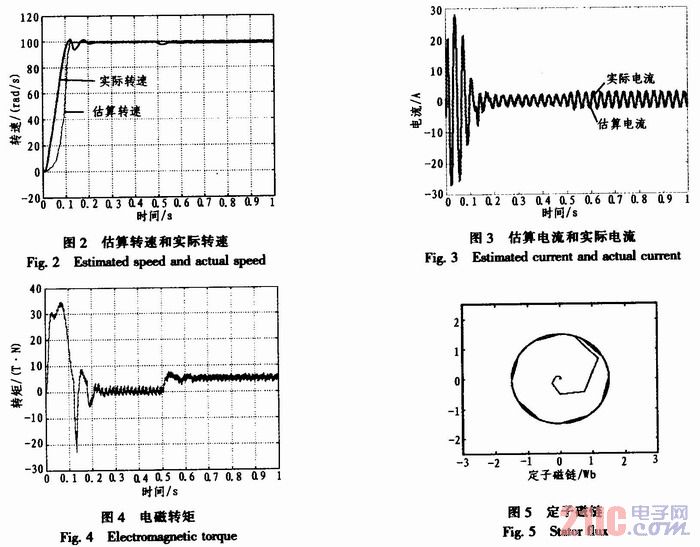
從仿真波形圖2對(duì)比可以看出,，采用無(wú)速度傳感器" title="無(wú)速度傳感器">無(wú)速度傳感器控制算法后控制過(guò)程的上升時(shí)間比有速度傳感器控制稍微長(zhǎng)一些,，但仍能滿足系統(tǒng)性能指標(biāo)要求。系統(tǒng)進(jìn)入穩(wěn)定后無(wú)速度傳感器控制的效果和有傳感器控制是一致的,。圖4顯示的是突加負(fù)載后,，從圖3看出定子電流幅值穩(wěn)定，轉(zhuǎn)速變化很小并很快恢復(fù)穩(wěn)定,，輸出轉(zhuǎn)矩能很快達(dá)到給定負(fù)載轉(zhuǎn)矩,，體現(xiàn)了DTC控制系統(tǒng)轉(zhuǎn)矩響應(yīng)快的特點(diǎn)，由此可見(jiàn)電機(jī)在運(yùn)行過(guò)程中,，受到各種擾動(dòng)時(shí),，電機(jī)轉(zhuǎn)速穩(wěn)定性好，可以滿足對(duì)控制特性的要求,。
EKF算法在異步電機(jī)轉(zhuǎn)子速度估計(jì)的應(yīng)用過(guò)程中采用直接更新系統(tǒng)狀態(tài)量和協(xié)方差矩陣的方法,，可以避免直接計(jì)算最大值動(dòng)態(tài)范圍較大的增益矩陣Kk。利用EKF算法的關(guān)鍵在于協(xié)方差矩陣Q和R的選取,。Q與模登誤差,、系統(tǒng)分布、A／D量化誤差有關(guān)；R與電流傳感器噪聲以及A／D變換器的編碼誤差有關(guān),。
4 結(jié)論
從算法分析和系統(tǒng)仿真分析討論的結(jié)果,，可以得出擴(kuò)展卡爾曼算法在無(wú)速度傳感器應(yīng)用中的優(yōu)點(diǎn)是：利用擴(kuò)展卡爾曼濾波器可以不必了解電機(jī)的機(jī)械參數(shù)知識(shí)(可以克服電機(jī)參數(shù)反應(yīng)靈敏的問(wèn)題)，在電機(jī)啟動(dòng)過(guò)程中不必知道電機(jī)轉(zhuǎn)子初始位置(可以解決電機(jī)的啟動(dòng)問(wèn)題),，此外,，EKF算法可以確保系統(tǒng)的全局穩(wěn)定性(其他一些通過(guò)狀態(tài)觀測(cè)器實(shí)現(xiàn)電機(jī)無(wú)速度傳感器控制的方法，通常僅在標(biāo)稱(chēng)狀態(tài)的軌跡上將電機(jī)非線性化,，不能保證系統(tǒng)的全局穩(wěn)定性),，而且整個(gè)系統(tǒng)易于數(shù)字化實(shí)現(xiàn)。但是擴(kuò)展卡爾曼算法復(fù)雜,，需要矩陣求逆運(yùn)算,，計(jì)算量大，為滿足實(shí)時(shí)控制的要求,，需要高速,，高精度的數(shù)字信號(hào)處理器。另一方面,，擴(kuò)展卡爾曼濾波器要用到很多隨機(jī)誤差的統(tǒng)計(jì)參數(shù),，由于模型復(fù)雜，涉及因素多,，使得分析這些參數(shù)的工作比較困難,，需要通過(guò)大量調(diào)試才能確定合適的隨機(jī)參數(shù)，而且調(diào)速范圍有一定的局限性,，只適合中高速調(diào)速系統(tǒng),。