為克服滑?？刂频倪@些不足，人們嘗試各種方法,，達到消除穩(wěn)態(tài)誤差的目的,。如文獻[8]采用時變切換面方程,；文獻[9]則將傳統(tǒng)的PID控制模式巧妙地應(yīng)用到切換面方程上，得到了只含有輸出電壓誤差一個變量的比例,、微分和積分的線性組合的滑模面方程,，以實現(xiàn)控制輸出電壓的目的；文獻[10]則采用補償網(wǎng)絡(luò),，對等價控制進行修正,，即所得到新的等價控制中已考慮了補償網(wǎng)絡(luò)的影響。目前尚未見有報道,，在實現(xiàn)DC/DC開關(guān)變換器滑模變結(jié)構(gòu)控制方案時,，考慮削弱高頻抖動的控制方案。從理論上分析,，引入變結(jié)構(gòu)趨近律[11],，將會簡化控制的確定，同時有助于改善系統(tǒng)的品質(zhì),。但在實際控制中,，如何利用變結(jié)構(gòu)趨近律來實現(xiàn)變結(jié)構(gòu)控制，達到削弱乃至消除抖動的目的,，卻很少被利用或涉及到,。
鑒于此，本文針對Boost電路工作于CCM模式提出了一種能夠動態(tài)地對滑模誤差進行修正,，從而動態(tài)地補償控制量的大小,，達到減少穩(wěn)態(tài)誤差，削弱高頻抖動的控制方案,，實現(xiàn)系統(tǒng)一些良好的控制品質(zhì),。
2Boost電路的滑模變結(jié)構(gòu)控制
Boost電路如圖1所示?？刂频哪康氖峭ㄟ^控制有源開關(guān)器件的占空比大小,，使系統(tǒng)狀態(tài)穩(wěn)定在期望值Xd（工作點）。
2．1控制算法
Boost電路工作于CCM模式時電路的狀態(tài)方程
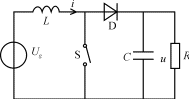
圖1Boost變換器
等價控制是在理想切換條件下實現(xiàn)理想滑模運動,。而實際控制中,，由于切換器件的慣性，開關(guān)延時等非理想切換因素,，滑模運動將不會在S=0的切換面上運動,，而是在其鄰域Δ內(nèi)運動。
換句話說,，引入Δu是為了修正由于實際系統(tǒng)的非理想因素造成的非理想切換而造成滑動模態(tài)誤差的,。代入式（3）， 顯然，當Δu≠0,，則≠0,。為滿足滑模到達條件以及改善系統(tǒng)的動態(tài)品質(zhì)，通過選擇的恰當形式,，保證系統(tǒng)到達條件s.<0成 立 ,， 以 期 系 統(tǒng) 以 某 種 方 式 趨 向 切 換 面 ， 形 成 滑 動 模 態(tài) ,。 這 里 通 過 引 入 趨 近 律 〖 11〗
因此,，Boost電路工作于CCM模式時的滑模變結(jié)構(gòu)控制律原則上，從物理意義上看,，相當于電路中的占空比,。即實際中的大小將受變換器本身物理本質(zhì)的限制，∈(0,1),。
2．2K1,、K2系數(shù)的選擇
由式（10）可見，Δu的大小與K1與K2的系數(shù)有關(guān),。理論上,，只要K1和K2不小于零，則滑動模態(tài)將穩(wěn)定,。但是K1取值過大,，則系統(tǒng)到達切換面的速度將很大，容易引起系統(tǒng)較大幅度的抖動,；K1取值過小，則控制的過渡過程長,。所以,，控制的過渡過程與動態(tài)品質(zhì)的好壞，更多的由系數(shù)K1決定,，線性項—K2S只是在一定程度上能緩和系統(tǒng)沖向切換面的速度,。希望系統(tǒng)趨近切換面的速度大小能自動根據(jù)由系統(tǒng)狀態(tài)所確定的s距離切換面s=0的大小來確定。因此,，采用以下方式確定系數(shù)K1和K2,。
其中，T是Boost變換器的開關(guān)工作周期,。
這里我們強調(diào)不同時刻取不同的K1（m）值,。
為確保K1(m)>0,K2的取值范圍：0≤K2≤fS(15)
2.3實際控制中的物理約束
對Boost電路，我們是以占空比作為控制量,，它必須受Boost電路本身的物理性質(zhì)的限制,。當控制量的大小超出（0，1）的范圍時，我們必須在控制方案中對控制量的大小加以約束,。Boost電路的直流分析表明,，其占空比與其直流解I和U的大小成反比。為提高控制的響應(yīng)速度,，同樣,，這里我們采用動態(tài)改變受約束的控制量的大小。
即約束控制量的大小依開關(guān)工作周期衰減,。
綜上所述,，我們得到Boost電路工作于CCM模式時第m個工作周期的滑模變結(jié)構(gòu)控制律
取元件參數(shù)為：L=6mH,C=45μF,R=30Ω,Ug=37.5V,fS=10kHz，開環(huán)占空比D取0.25,。直流分析結(jié)果得：U=50V,，I=2.2A。取期望穩(wěn)定工作點為：Xd=[2.250〗T,。取控制參數(shù)：KC=[－1501]T,K2=800,。分別對Boost電路的起動過程和其穩(wěn)態(tài)系統(tǒng)有擾動變化的情況進行仿真研究。
圖2是Boost電路采用不同的控制律下起動瞬態(tài)過程,，圖3是起動過程的相平面圖,，其中“0”是期望工作點Xd所在的位置。由圖顯然可以看到采用式（6）的等價控制作為實際滑?？刂坡蓵r（曲線3）,，系統(tǒng)會存在明顯的穩(wěn)態(tài)誤差，系統(tǒng)最后不會趨向切換面,，也不會運動到期望工作點（圖3中虛線）,。而采用式（17）的控制算法則可以很好地解決該問題（曲線1和圖3中實線），并有效地解決滑?？刂浦械母哳l抖動問題,。如果式（17）的控制算法中，控制參數(shù)取常數(shù),，而忽略線性項—K2S,，即不采用動態(tài)修正滑模誤差的控制算法時，動態(tài)響應(yīng)時間會很長,，K1的取值會很大,。例如當K1=10000時，起動瞬態(tài)過程如圖2中曲線2所示,。
圖4和圖5是考慮系統(tǒng)擾動情況的瞬態(tài)特性曲線,。圖4中，系統(tǒng)在前階段輸入電壓的擾動突然由正常電壓降低50％,，在后階段輸入電壓的擾動突然由正常電壓升高10％,。圖5中,，系統(tǒng)在前階段負載的擾動突然由正常負載增加100％，在后階段負載的擾動突然由正常電壓降低50％,。從圖中看到,，無論系統(tǒng)擾動如何變化，仍然可以保證系統(tǒng)的穩(wěn)定,，控制系統(tǒng)具有較好的魯棒性,。
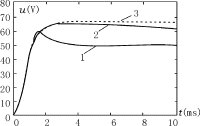
圖2不同控制下起動瞬態(tài)過程的比較
圖3起動過程相平面圖
圖4輸入電壓擾動瞬態(tài)過程
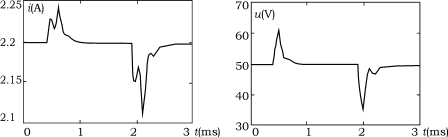
圖5負載擾動瞬態(tài)過程
4結(jié)論
在實現(xiàn)滑模變結(jié)構(gòu)控制時必須考慮實際控制中的非理想切換條件以及實際控制量的物理約束。本文提出的滑模變結(jié)構(gòu)控制算法簡單,，對Boost電路的起動過程和穩(wěn)態(tài)時系統(tǒng)有擾動變化時情況進行仿真,，結(jié)果表明，本文的控制方案可以減少系統(tǒng)超調(diào),，縮短過渡過程時間,，改善系統(tǒng)的動態(tài)品質(zhì)，并有效地解決滑?？刂浦械母哳l抖動問題,；穩(wěn)態(tài)時，即使系統(tǒng)輸入電壓或者輸出負載有較大擾動,，仍然可以保證系統(tǒng)的穩(wěn)定,，控制系統(tǒng)具有較好的魯棒性。