摘  要： 基于隱馬爾可夫模型HMM提出了一種新的信息工程監(jiān)理質(zhì)量控制方法，并建立了模型,。該模型將信息工程質(zhì)量監(jiān)理過程視為兩層隨機過程,，通過抽取監(jiān)理過程的特征，將隱馬爾可夫模型的5個要素與質(zhì)量監(jiān)理過程相對應(yīng),。利用該模型可以求解質(zhì)量度量要素觀測序列和質(zhì)量狀態(tài)的匹配度,，通過調(diào)整模型的初始參數(shù)可以將該模型應(yīng)用于不同的監(jiān)理軟件，并以概率的形式預(yù)測監(jiān)理過程的結(jié)果,。通過仿真實驗,，驗證了該方法應(yīng)用于信息工程監(jiān)理質(zhì)量控制的可行性。
關(guān)鍵詞： 信息工程監(jiān)理,；質(zhì)量控制,；隱馬爾可夫模型；前向算法

    目前,，用于信息工程監(jiān)理[1]質(zhì)量控制的方法主要有基于模糊理論,、基于因素神經(jīng)網(wǎng)絡(luò)、基于灰色系統(tǒng)理論[2]和基于模糊因素神經(jīng)網(wǎng)絡(luò)等,；軟件質(zhì)量的度量模型主要有Boehm模型,、McCall模型和ISO/IEC9126模型[3]等。這些方法和模型都能較好地適應(yīng)于靜態(tài)問題的解決,，但監(jiān)理人員只有針對信息工程監(jiān)理各個階段實施全過程的動態(tài)監(jiān)理,，才能使影響信息系統(tǒng)質(zhì)量的要素在開發(fā)過程中處于受控狀態(tài)。隱馬爾可夫模型HMM(Hidden Markov Model)是一種雙重隨機過程,，能夠解決隨機不確定問題,，在很多方面已有廣泛應(yīng)用[4],，具有理論研究透徹、算法成熟,、效率高,、效果好、易于訓(xùn)練等特點,，作為一種有效的概率工具,，已成為信息抽取領(lǐng)域中一個新的研究方向[5]。本文通過對信息工程質(zhì)量監(jiān)理過程特點的分析,，將隱馬爾可夫模型映射到質(zhì)量監(jiān)理中,，利用前向算法估計出在該模型下觀測事件序列發(fā)生的概率，從而在一定程度上有助于對軟件質(zhì)量進行定量控制,。
1 模型的建立
1.1 特征提取
    隱馬爾可夫模型由兩個部分組成[6]：一個是隱蔽的（不可觀測的）,、具有有限狀態(tài)的馬爾可夫鏈[7]，另一個是與馬爾可夫鏈的每一狀態(tài)相關(guān)聯(lián)的觀察事件的隨機過程（可觀測的）,。
    將隱馬爾可夫模型映射到信息工程監(jiān)理質(zhì)量評估模型上,，即一個軟件的質(zhì)量狀態(tài)是無法直接觀察到的，但是可以通過分析與這個軟件相關(guān)的質(zhì)量度量要素,，估算該軟件的質(zhì)量狀態(tài),，從而進一步得到其量化的評判值。信息化工程監(jiān)理國標中的信息化工程監(jiān)理規(guī)范技術(shù)參考模型[8]將信息工程質(zhì)量監(jiān)理分為工程招標,、工程設(shè)計,、工程實施和工程驗收四個階段。各個階段的軟件質(zhì)量狀態(tài)構(gòu)成一個馬爾可夫鏈,，度量要素序列是一個隨機過程,，每一個度量要素會對軟件的質(zhì)量狀態(tài)的轉(zhuǎn)移帶來一定影響，這樣,，度量要素序列和軟件的質(zhì)量狀態(tài)之間就構(gòu)成了一個隱馬爾可夫模型,。通過觀察信息工程監(jiān)理全過程各個階段的度量要素，每個階段都可以得到一個隨機的度量要素序列,，這樣就可以計算軟件的質(zhì)量狀態(tài)和評判值,。
    軟件質(zhì)量目標控制按照分層法分解為人、軟件元,、開發(fā)方法,、設(shè)備及材料和工程環(huán)境五個度量要素，軟件質(zhì)量狀態(tài)依據(jù)各度量要素分為優(yōu),、良,、中、差四個決斷因子,，如果再定義出它們之間的概率轉(zhuǎn)換關(guān)系,，就會得到由這兩組狀態(tài)構(gòu)成的隱馬爾可夫模型（如圖1所示）,。

    根據(jù)該HMM模型，可以在沒有直接觀測軟件質(zhì)量的情況下根據(jù)度量要素的分布來推測軟件質(zhì)量的變化情況,。

    如果能較為準確地計算軟件質(zhì)量處于何種狀態(tài),，則可以定量分析軟件的質(zhì)量情況。軟件質(zhì)量狀態(tài)之間的轉(zhuǎn)移見圖2,。

    由圖1可以直觀看出,，度量軟件質(zhì)量的要素有5個，用V={P,，U,，M，F(xiàn),，E}表示,，ν1=P(People)，表示度量要素人的因素,；ν2=U(Units)，表示度量要素軟件元質(zhì)量,；ν3=M(Methods),，表示度量要素開發(fā)方法；ν4=F(Facilities),，表示度量要素設(shè)備及材料,；ν5=E(Environment)，表示度量要素工程環(huán)境,。設(shè)質(zhì)量度量要素觀測序列為O={o1,，o2，o3,，o4},，其中ot∈V。
    設(shè)軟件質(zhì)量情況在信息工程監(jiān)理開始階段狀態(tài)為π,，它是一個向量,，表示在信息工程監(jiān)理工程招標階段軟件質(zhì)量處于各個狀態(tài)的概率，π={π1,，π２,，π３，π４},，πi=P(q1=si),，1≤i≤4。對于工程招標階段,，可以根據(jù)信息工程監(jiān)理協(xié)同工作平臺下的模糊因素神經(jīng)網(wǎng)絡(luò)質(zhì)量評估方法得到一個默認值,，之后的每一階段,，通過Trans和Obs可以計算出當(dāng)前軟件質(zhì)量處于各種狀態(tài)的概率st=(r1，…,，r4),，將此概率作為下一階段的初始狀態(tài)。在t階段,，狀態(tài)分布表示為rt={rt(i)},，1≤i≤4，狀態(tài)的分布概率公式為：rt(i)=P(qt=si|λ),。再引入一個代價向量C[10],，代表軟件在每個狀態(tài)的質(zhì)量值，則可以將軟件狀態(tài)的定性分析轉(zhuǎn)化為定量分析,。
    設(shè)Trans為軟件質(zhì)量狀態(tài)轉(zhuǎn)換矩陣,，即質(zhì)量狀態(tài)之間轉(zhuǎn)換的概率組成的矩陣，包含4行4列,，aij表示在t階段質(zhì)量狀態(tài)為si,，那么到t+1階段質(zhì)量狀態(tài)為sj的概率，即aij=P(qt+1=sj|qt=si),，1≤i,，j≤4。
    定義Obs為當(dāng)軟件處于某一個特定質(zhì)量狀態(tài)時觀測到某種度量要素的概率矩陣,，bj（k）表示在階段t,，軟件質(zhì)量處于sj狀態(tài)觀測到度量要素νk的概率，1≤k≤5,，1≤j≤4,。
2 基于前向算法的模型應(yīng)用
    根據(jù)得到的觀察序列O={o1，o2,，o3,，o4}和模型λ=(π，Trans,，Obs)可以計算出在該模型下觀察事件序列發(fā)生的概率P(O|λ),。P(O|λ)評價了給定模型?姿與給定觀測序列匹配的程度。
　對隱馬爾可夫模型而言,，狀態(tài)轉(zhuǎn)換序列是隱藏的,，一個觀測序列可能由任何一種狀態(tài)轉(zhuǎn)換序列產(chǎn)生。因此要計算一個觀測序列的概率值,，就必須考慮所有可能的狀態(tài)轉(zhuǎn)換序列,。
    窮舉搜索的時間復(fù)雜度是2TNT，前向算法的時間復(fù)雜度是2N2T,，其中T指的是觀察序列長度,，N指的是隱藏狀態(tài)數(shù)目,。對于信息工程監(jiān)理質(zhì)量控制，N=4,，T=4,，如果利用窮舉搜索算法，復(fù)雜度相對會比較大,，可以采用前向算法來降低復(fù)雜度,。

    給定這種算法，對于已知的一個度量要素觀察序列,，可以直接用來確定在一些隱馬爾可夫模型中哪一個最好地描述了它,，即先用前向算法評估某一個給定的λ，然后通過多次調(diào)整參數(shù)λ來提高評估的概率,，進而通過實時調(diào)整信息工程監(jiān)理中的質(zhì)量的度量要素的比例來達到提高軟件質(zhì)量控制的目的,。
3 仿真實驗
    實驗數(shù)據(jù)來源于信息工程監(jiān)理協(xié)同工作平臺（IPSS）下的數(shù)據(jù)庫。實驗環(huán)境為Eclipse和Java開源工具包jahmm-0.6.1,。文中使用狀態(tài)數(shù)為N=4,，觀測值數(shù)為M=5的隱馬爾可夫模型進行檢驗。
    在信息工程監(jiān)理中,，每個階段軟件所處的質(zhì)量狀態(tài)與前一階段所處的質(zhì)量狀態(tài)有關(guān),，即前一階段的質(zhì)量狀態(tài)會影響下一階段質(zhì)量狀態(tài)出現(xiàn)的概率。
    初始質(zhì)量狀態(tài)概率分布：π=(0.3,，0.3，0.2,，0.2)
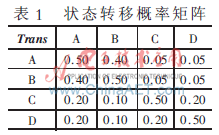
    四個質(zhì)量狀態(tài)兩兩之間轉(zhuǎn)化的概率如表1所示,。

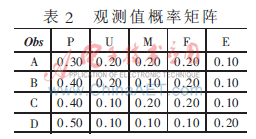
    軟件質(zhì)量處于某個狀態(tài)時，度量要素所占的比例有一定的規(guī)律性,。度量要素觀測值概率分布如表2,。

    下面根據(jù)軟件質(zhì)量初始狀態(tài)、表1和表2的數(shù)據(jù),，估計狀態(tài)序列O={P,，U，M,，F(xiàn)}出現(xiàn)的概率,。假設(shè)P為工程招標階段觀測到的主導(dǎo)要素，U為工程設(shè)計階段觀測到的主導(dǎo)要素,，M為工程實施階段觀測到的主導(dǎo)要素,，F(xiàn)為工程驗收階段觀測到的主導(dǎo)要素。
    在模型λ下,，在t時刻觀測事件是ot,、狀態(tài)是si的概率如表3所示,，每個階段的四個概率對應(yīng)四個質(zhì)量狀態(tài)。

    本文通過對隱馬爾可夫理論的分析,，建立了用于質(zhì)量控制的隱馬爾可夫模型,，并嘗試基于該模型對信息工程監(jiān)理進行質(zhì)量控制。本文提出的隱馬爾可夫質(zhì)量控制模型只是用于控制信息工程監(jiān)理4個階段的5個基本要素,，模型稍顯粗糙,。如何基于隱馬爾可夫模型或其他擴展模型與信息工程監(jiān)理質(zhì)量控制完全的整合，以及如何利用模型進行質(zhì)量評估并對模型進行訓(xùn)練還需要進一步的探索研究,。
參考文獻
[1] 劉宏志,，葛迺康.信息化工程監(jiān)理[M].北京：中國電力出版社，2009.
[2] 劉宏志,，楊建軍.基于灰色系統(tǒng)理論的軟件工程監(jiān)理研究[J].經(jīng)濟管理,，2007，29(18).
[3] 周建.關(guān)于軟件質(zhì)量的定量評估的研究[D].成都：電子科技大學(xué),，2007.
[4] 胡可,，張大力.一類廣義隱馬爾可夫模型的建模與參數(shù)估計[J].中國科學(xué)院研究生院學(xué)報，2005,，22(2)：210-217.
[5] 洪流,，張巍，肖明軍,，等.一種改進的基于HMM的信息抽取模型[J].模式識別與人工智能,，2004，17(3)：347-351.
[6] 翟琳琳,，陳儀香.隱馬爾可夫模型在智能學(xué)習(xí)系統(tǒng)中的應(yīng)用[J].計算機工程與應(yīng)用,，2007，43(6)：178-180.
[7] Wojciech Pieczynski. Pairwise Markov Chains[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,， 2003,， 25(5)： 634-639.
[8] 中國國家標準化管理委員會.信息化工程監(jiān)理規(guī)范——第5部分：軟件工程監(jiān)理規(guī)范[S].中華人民共和國國家標準，GB/T 19668.5-2007,，ICS.35.020,，L01.
[9] LEE H K， KIM J H. An HMM-Based Threshold Model Approach for Gesture Recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,， 1999,， 21(10)：961-973.
[10] 董靜.改進的HMM網(wǎng)絡(luò)安全風(fēng)險評估方法研究[D].武漢：華中科技大學(xué)，2008.
[11] 彭子平,，張嚴虎,，潘露露.隱馬爾可夫模型原理及其重要應(yīng)用[J].計算機科學(xué)，2008，35(4).