0 引言
TI公司的C2000系列DSP以其出色的性能、豐富的片上外設(shè)在工業(yè)自動(dòng)化、電機(jī)控制、工業(yè)生產(chǎn)領(lǐng)域得到廣泛應(yīng)用。TMS320F2812是C2000系列中性能出色的一個(gè),F(xiàn)2812片上集成了12位16通道的數(shù)/模轉(zhuǎn)化器,理論上精度可以達(dá)到0.1%以上。但實(shí)際上由于增益誤差(<5%)和偏移誤差(<2%)的存在,使得精度只能在5%左右,所以必須對(duì)ADC進(jìn)行校正。
傳統(tǒng)的對(duì)于ADC的校正方法是在兩路通道輸入已知標(biāo)準(zhǔn)電壓,根據(jù)兩點(diǎn)確定一條直線的原理,確定出AD轉(zhuǎn)換的曲線,并以此校正轉(zhuǎn)化值。但由于在校正過(guò)程中存在偶然因素的影響,使得這種校正方法精度只能達(dá)到3%左右。對(duì)此,提出了利用最小二乘法和線性回歸的思想進(jìn)行校正的方法,通過(guò)對(duì)多個(gè)測(cè)量點(diǎn)的分析計(jì)算,找出最佳的擬合曲線,使得總體的均方誤差最小。
最小二乘法是高斯于1809年提出的,在多學(xué)科領(lǐng)域中獲得廣泛應(yīng)用的數(shù)據(jù)處理方法。用最小二乘法估測(cè)未知參數(shù),可以有效消除測(cè)量中粗大誤差和系統(tǒng)誤差的影響。回歸分析是英國(guó)統(tǒng)計(jì)學(xué)家高爾頓在18*首先提出的。一元線性回歸是利用數(shù)理統(tǒng)計(jì)中的回歸分析,來(lái)確定兩種或兩種以上變數(shù)間相互依賴的定量關(guān)系的一種統(tǒng)計(jì)分析方法之一,運(yùn)用十分廣泛。一般來(lái)說(shuō),線性回歸都可以通過(guò)最小二乘法求出其方程,可以計(jì)算出對(duì)于y=bx+a的直線。
1 校正原理與實(shí)現(xiàn)方案
DSP的ADC模塊的輸入、輸出是線性關(guān)系,理想情況下,輸入輸出方程應(yīng)該是y=x。但實(shí)際上,ADC模塊是存在增益誤差和偏移誤差的,其中增益誤差是實(shí)際曲線斜率和理想曲線斜率之間的偏差,偏移誤差是0 V輸入時(shí)實(shí)際輸出值與理想輸出值(0 V)之間的偏差。F2812的ADC模擬輸入電壓為0~3 V,輸出為0~4 095,模擬輸入與數(shù)字輸出之間的對(duì)應(yīng)關(guān)系為:數(shù)字輸出值=4 095×(模擬輸入值-參考電壓值)/3.0ADC模塊輸入/輸出特性曲線如圖1所示。
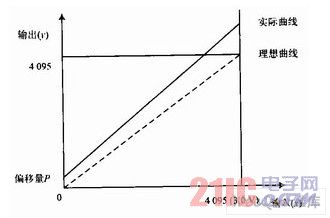
圖1 ADC模塊輸入/輸出特性曲線
F2812的ADC共有輸入通道16個(gè),由于通道之間的誤差會(huì)在±0.2%以內(nèi),所以可以任選其中的6路通道作為校正輸入端,并分別輸入6個(gè)不相等的標(biāo)準(zhǔn)直流參考電壓。通過(guò)在程序中定義結(jié)構(gòu)體變量讀取轉(zhuǎn)化后的值,得到6組輸入/輸出平面上的坐標(biāo)點(diǎn)。然后利用最小二乘和一元線性回歸思想處理數(shù)據(jù),求出的擬合最佳曲線,使得各個(gè)坐標(biāo)點(diǎn)到該最佳曲線的距離的平方和(殘差平方和)最小。
2 最小二乘法和一元線性回歸
2.1 最小二乘原理
對(duì)于線性模型,如果有t個(gè)不可測(cè)量的未知量,理論上,可對(duì)與該t個(gè)未知量有函數(shù)關(guān)系的直接測(cè)量量進(jìn)行t次測(cè)量,即可得到函數(shù)關(guān)系。但由于測(cè)量數(shù)據(jù)不可避免地包含著測(cè)量誤差,所得到的結(jié)果也必定含有一定的誤差。為了提高所得結(jié)果的精度,可以把測(cè)量次數(shù)增加到n(n>t),以利用抵償性減小隨機(jī)誤差的影響。
高斯認(rèn)為,根據(jù)觀測(cè)數(shù)據(jù)求取未知參數(shù)時(shí),未知參數(shù)最合適數(shù)值應(yīng)是這樣的數(shù)值,即選出使得模型輸出與觀測(cè)數(shù)據(jù)盡可能接近的參數(shù)估計(jì),接近程度用模型輸出和數(shù)據(jù)之差的平方和來(lái)度量。這就是最小二乘的基本思想。最小二乘法原理指出,最精確的值應(yīng)在使殘余誤差平方和最小的條件下求得。
2.2 一元線性回歸原理
一元線性回歸是處理2個(gè)變量之間的關(guān)系,即兩個(gè)變量x和y之間若存在線性關(guān)系,則通過(guò)試驗(yàn),分析所得數(shù)據(jù),找出兩者之間函數(shù)曲線。也就是工程上常遇到的直線擬合問(wèn)題。
3 實(shí)驗(yàn)方案與結(jié)果分析
3.1 實(shí)驗(yàn)方案
實(shí)驗(yàn)利用F2812開(kāi)發(fā)板和DSP調(diào)試軟件CCS2.0完成。用穩(wěn)定信號(hào)源產(chǎn)生6個(gè)標(biāo)準(zhǔn)電壓,分別為0.2 V,0.5 V,1.0 V,1.5 V,2.0 V,2.5 V,輸入通道選為A0,A1,A2,B0,B1,B2。ADCL0引腳接電路板的模擬地,與模擬輸入引腳相連的信號(hào)線應(yīng)該避開(kāi)數(shù)字信號(hào)線,以減少數(shù)字信號(hào)對(duì)模擬信號(hào)的干擾。輸入電路如圖2所示。
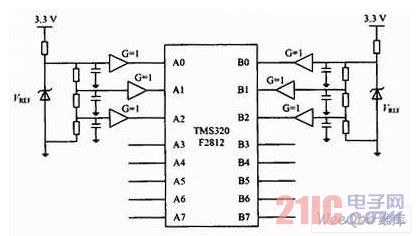
圖2 輸入電路
3.2 校正算法
設(shè)ADC模塊的輸入/輸出曲線為y=a+bx,輸入電壓值為xi,對(duì)應(yīng)的轉(zhuǎn)化輸出值為yi。由最小二乘估計(jì)算法可得方程:
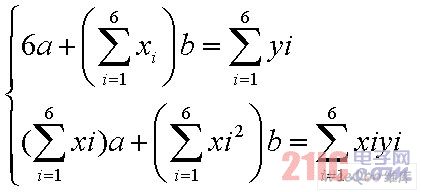
解此方程組即可得到a,b的估計(jì)值:
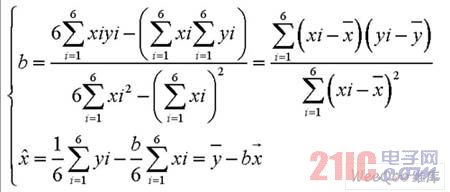
式中,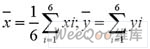 這樣這樣便得到了最佳的擬合曲線(回歸方程):
這樣這樣便得到了最佳的擬合曲線(回歸方程):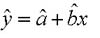 于是可以用此方程進(jìn)行轉(zhuǎn)化值校正。
于是可以用此方程進(jìn)行轉(zhuǎn)化值校正。
3.3 實(shí)驗(yàn)數(shù)據(jù)處理
將實(shí)驗(yàn)獲得的6組數(shù)據(jù)利用上述最小二乘法和線性回歸方法進(jìn)行處理,得到a,6的最小二乘估計(jì)值分別為,于是回歸方程為:y=0.003 612+1.039 091x。以回歸方程為標(biāo)準(zhǔn),由x=(y-0.003 612)/1.039 091可以計(jì)算出校正后的轉(zhuǎn)化值,并與未轉(zhuǎn)化的值進(jìn)行比較,結(jié)果如表1所示。
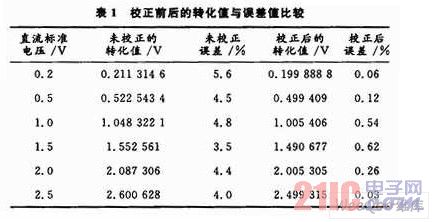
在Excel中,繪制出未校正輸入/輸出分布點(diǎn),和回歸曲線,如圖3所示。
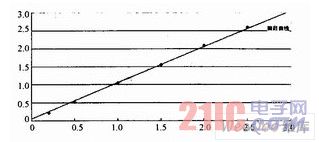
圖3 回歸曲線示意圖
3.4 結(jié)果分析
由表1和圖3可以看出,如果不采取校正措施,則F2812的ADC模塊會(huì)存在5%左右的相對(duì)誤差;而采用提出的校正方法,可以將誤差下降到1%以下。這就大大提高了A/D轉(zhuǎn)化的精度,對(duì)于對(duì)控制要求精度很高的場(chǎng)合,犧牲ADC模塊的6個(gè)通道,得到比較高的轉(zhuǎn)化精度,還是非常必要而且值得的。
4 結(jié)語(yǔ)
在此提出一種采用最小二乘法和線性回歸校正DSP的ADC模塊的方法,實(shí)驗(yàn)證明此方法可以大大提高轉(zhuǎn)化精度,有效彌補(bǔ)了DSP中AD轉(zhuǎn)化精度不高的缺陷。此方法硬件電路簡(jiǎn)單,成本代價(jià)較低,具有很高的推廣和利用價(jià)值。

