摘 要: 二維傅立葉變換" title="傅立葉變換">傅立葉變換" title="快速傅立葉變換" title="快速傅立葉變換">快速傅立葉變換">快速傅立葉變換(FFT)在一個傳統(tǒng)概念的處理機上實現時,需要芯片具有更多的邏輯資源。本文給出了基于FPGA的自定義處理機(CCM)的二維FFT算法和實現。在CCM的Splash-2平臺上實現了二維FFT,計算速度達到180Mflops,最快速度超過Sparc-10工作站的23倍。同時,對于一個N×N圖像,這種實現方法可以滿足二維FFT所需要的O(N2log2N)次的浮點算術運算。
關鍵詞: 自定義處理機(CCM);二維;快速傅立葉變換(FFT); 圖像;Splash-2
?
當被處理的圖像像素相對較小時,可以直接采用空間域濾波的方法。但隨著像素的增多,計算量也隨之增大。針對這種情況,本文對像素較大的圖像,采用了一種將圖像先從空域轉換到頻域,執(zhí)行點到點的乘法濾波,然后通過反傅立葉變換,將頻域內濾波器圖像再轉換到空間域的方法。在此基礎上,對二維快速傅立葉變換采用了基于FPGA的CCM的Splash-2平臺實現方式,目的是為了對視頻信號進行實時濾波。實現過程中需要對浮點數" title="浮點數">浮點數進行計算,采用了CCM可以自定義數據格式和算法數據流以滿足應用的需要。
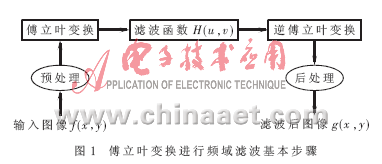
1 用傅立葉變換進行圖像濾波
圖1是用快速傅立葉變換進行圖像濾波處理的實現過程[1],其中,預處理階段包括確定圖像大小、獲得填充參數和生成一個濾波函數等過程;后處理階段包括計算結果的實部" title="實部">實部,修剪圖像以及將圖像進行轉換等操作,其他部分將在以下環(huán)節(jié)分別進行介紹。
?
1.1 離散傅立葉變換(DFT)
一個N×N圖像的二維的DFT,f(x,y)定義為:
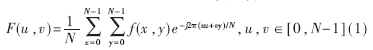
二維的DFT變換可以分解成多個一維的傅立葉變換,則(1)式等同于:
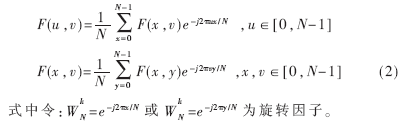
公式(1)、(2)表明一個N×N的二維DFT可以通過先進行N個一維DFT(行),然后再進行另外N個一維DFT(列)來計算,即所謂的行列分解法[2]。
1.2 快速傅立葉變換(FFT)
? 執(zhí)行一個N點DFT所需的復雜乘法和加法運算次數與N2成正比。由于一維DFT可以被分解,所以進行乘法與加法運算的次數正比于N×log2N。而FFT算法通過“分而治之”的方法來實現其較高的計算效率。通過時間與頻率采樣的分組,具有N個值的DFT運算可以表示成兩點DFT的組合方式。這兩點DFT稱為蝶形運算,它需要一次復乘和兩次復加來實現。蝶形結構的符號如圖2所示(左側:基2的蝶形結構)。
?
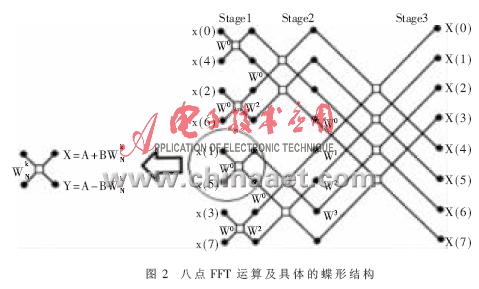
用FFT“分而治之”的方法,一個8點的FFT的計算如圖2所示。N點FFT的每一級運算由N/2基2的蝶形組成,總共有l(wèi)og2N次運算。因此,每個FFT共有(N/2)×log2N個蝶形結構。一個二維FFT可以拆分為兩組一維的DFT運算,且每個DFT可以用一維的FFT來計算。此外,數據以倒位序輸入而以正常的線性順序輸出。
2 浮點算法
2.1 浮點格式的表示
為了實現本文給出的FFT運算,在此設計了一個較小的18bit的浮點格式。用這種格式來滿足兩種特定要求:(1)動態(tài)范圍需要非常大,以便能夠準確地表示一個實數的大小、正負;(2)進入Splash-2平臺的XILINX 4010處理器的數據通道寬度為36bit,且每一個時鐘周期" title="時鐘周期">時鐘周期內都輸入復數的實部與虛部。基于這些要求,使用的浮點格式如圖3所示。
?

2.2 浮點加法減法與乘法
為了在每個時鐘周期產生一個結果,開發(fā)浮點加減法程序來實現管道化單元,所實現的浮點加法與減法算法與最傳統(tǒng)的處理器相似。
浮點乘法與整數乘法類似。因為浮點數是以“符號-數字”的形式存儲,乘法器僅需要處理無符號整數,與浮點加法器的結構類似[3],浮點乘法器單元也是每個時鐘周期產生一次結果,這種設計的瓶頸是整數乘法器。
本文將VHDL語言放在XILINX芯片相應開發(fā)工具ISE中進行編譯,同時給出時延、速度等相關參數。
浮點運算單元還與FIR濾波器組合一起使用。FFT運算以10MHz工作,轉換的結果存儲在Splash-2開發(fā)板的存儲器中。算術單元的最大時鐘速度至少可以工作在10MHz。
3 FFT的實現
本文從一個幀緩沖區(qū)得到連續(xù)的視頻圖像提供給FFT和IFFT參與并行計算從而構建出濾波算法。以下討論用于實現FFT、FFT中的蝶形操作以及濾波處理的再循環(huán)算法。
3.1 FFT再循環(huán)算法
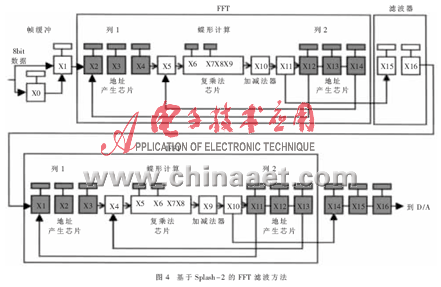
為了計算二維的FFT,需要設計一個通過蝶形運算的數據循環(huán)算法。圖4給出了相應的結構圖。
?
?
兩列存儲器用來存儲FFT的每一級運算的輸入輸出數據。每一列存儲器包括三個處理單元,用來把兩個18bit浮點數的實部與虛部存儲到它們的本地內存。由于本地內存只有16bit寬,先將兩個18bit浮點數值進行分割,然后按順序放在三個存儲單元中。為了計算輸入圖像的FFT,來自于幀緩沖區(qū)中的數據幀從8bit的整數被轉換為18bit的浮點數存儲在第一列中。在計算二維FFT時,首先計算圖像每一行的一維FFT,然后計算行變換后每一列的FFT。一維FFT的計算與圖2中所示方法相同。FFT的第一級通過從第一列存儲區(qū)以倒位序讀取數據采樣點的每一行,然后將它送給蝶形操作進行計算。蝶形計算的結果存儲在第二列存儲區(qū)。當第一級中的蝶形計算完成時,開始第二級計算,從第二列存儲區(qū)中順序讀取數據然后送入蝶形處理器,這一操作的結果存儲在第一列存儲區(qū)。這一循環(huán)方法通過從一個存儲區(qū)中讀數而在另一外存儲區(qū)存儲計算結果來進行。當圖中每一行一維FFT計算完時循環(huán)終止。第二組一維FFT與第一組以相同的方法進行計算,直到第二組的FFT計算完第一組的所有結果。當最后一次FFT的最后一級計算完時,數據從X11傳到X15進行濾波。一次完整的二維FFT過程包括2×N2×log2N次蝶形操作。
3.2 蝶形實現
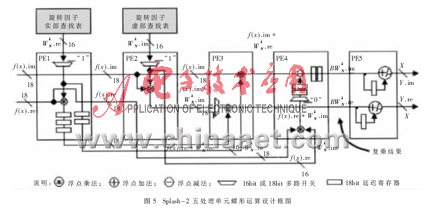
蝶形操作是FFT算法的核心。蝶形運算框圖如圖2所示,它包括了一次復乘與兩次浮點加法、減法。復乘包括4次乘法和兩次加減。每個時鐘周期內以10MHz進行8次浮點操作。蝶形操作的計算量為80Mflops。圖5表示在Splash-2平臺上如何將蝶形運算在5個處理單元之間進行分割計算。
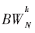 復乘的實部與虛部分別用下式來表示:
復乘的實部與虛部分別用下式來表示:

圖2中蝶形運算輸入A與輸入B如圖5中的f(x)所示。A值先送入計算,在下個時鐘周期再送入B的值。輸入A不與旋轉因子相乘而是通過多路選擇開關對它乘1加0無改變地通過循環(huán)運算。當B的實部與虛部送入時,它們依次通過4個處理單元來得到復乘結果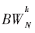 。處理單元1(PE1)讀出相應旋轉因子的實部并將它與B的實部相乘,計算結果與旋轉因子送到處理單元3(PE3),B的實部與虛部送到處理單元2(PE2)。PE2將B的虛部與相應旋轉因子相乘結果送入PE3。PE3從PE1中讀取B.re
。處理單元1(PE1)讀出相應旋轉因子的實部并將它與B的實部相乘,計算結果與旋轉因子送到處理單元3(PE3),B的實部與虛部送到處理單元2(PE2)。PE2將B的虛部與相應旋轉因子相乘結果送入PE3。PE3從PE1中讀取B.re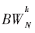 .re,把它與從PE2中讀取的B.im
.re,把它與從PE2中讀取的B.im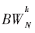 .im相加,得到復乘實部的最終結果
.im相加,得到復乘實部的最終結果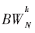 .re;復乘虛部
.re;復乘虛部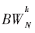 .im可用同樣的方法在PE3與PE4中得到。在第一個時鐘周期內將A與
.im可用同樣的方法在PE3與PE4中得到。在第一個時鐘周期內將A與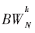 相加得到X,在第二個時鐘周期內將A減去
相加得到X,在第二個時鐘周期內將A減去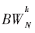 得到Y,這樣就完成了蝶形運算。
得到Y,這樣就完成了蝶形運算。
?
由于存儲器數據總線的寬度僅為16bit,在本地PE1、PE2的存儲器中無法存儲18bit格式的旋轉因子。因此從18bit浮點指數域中減去2bit來產生一個較小的16bit格式,而用歐拉定理可以將旋轉因子表示成正余弦函數的形式,因此浮點數的值將不會有大于0的指數。因此,指數域范圍從0~-31變化,這樣指數域的長度從7bit減到5bit。當旋轉因子被讀入處理單元時,在相應運算單元中進行一次從16bit格式到18bit格式的轉換即可。
3.3 濾波
當輸入圖像轉換到頻域時,矩陣濾波系數H(u,v)和轉換后的圖像可以通過濾波器得到濾波后的圖像。矩陣H(u,v)元素值的范圍為0~1.0,它與蝶形運算旋轉因子以相同的的存儲方式存儲在本地的存儲器中。濾波系數存儲在X15和X16芯片的本地存儲器中。濾波器芯片包括一個浮點乘法單元和濾波系數地址邏輯單元,X15與X16用來對轉換后圖像的實部和虛部分別進行濾波。
不同類型的濾波器如理想濾波器以及其他類型濾波器可以先計算,然后從宿主機下載到開發(fā)平臺的存儲器中。
由于CCM的靈活性,浮點格式可以通過自定義方式以最小的比特數來達到最大精度。利用Splash-2的并行結構,地址計算、蝶形運算以及濾波可以并行地進行計算。通過蝶形運算操作,每個時鐘周期內可以以10MHz的速度得到一個實數或復數結果。這種應用的性能類似于一個典型的DSP處理器所達到的性能。
參考文獻
[1] RAFAE1 C G,RICHARD E W,STEVEN L E.數字圖像處理.北京:電子工業(yè)出版社,2006.
[2] DAN E D,RUSSELL M M.多維數字信號處理.北京:科學出版社,1991.
[3] SHIRAZI N,WALTERS A P A.Quantitative analysis of floating point arithmetic on FPGA based custom computing?machines.IEEE Symposium on FPGAs for Custom Computing Machines,1995,(4).

