根據(jù)功率因數(shù)校正設(shè)備的基本電路分析混合功率因數(shù)校正的系統(tǒng)理論的正確性和他的實(shí)用性.根據(jù)Buck-boost 電路和Buck 電路作為基本變換器,,可以得到如下圖1A、2A,、3A 所示的PFC 電路,,如果考慮到隔離的需要,對(duì)應(yīng)有如圖1B,、2B,、3B 所示的PFC 電路。
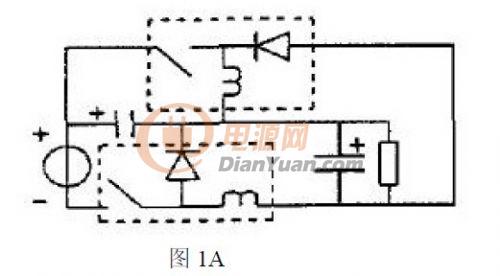
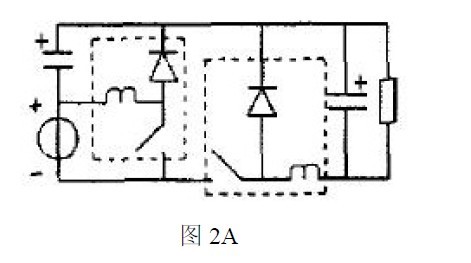
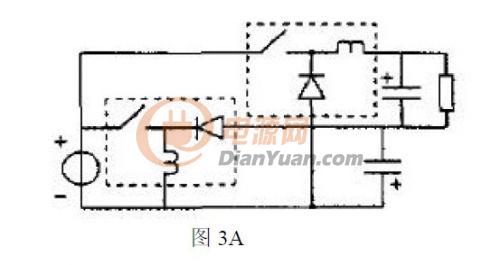
如果選擇兩個(gè)Buck-boost 電路作為基本變換器,,同理可以得到3A 所示的電路,??紤]到隔離的需要,有如圖3B 所示的PFC 電路,。
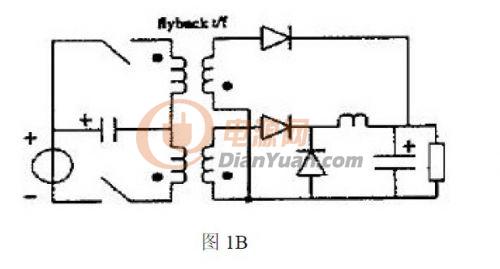
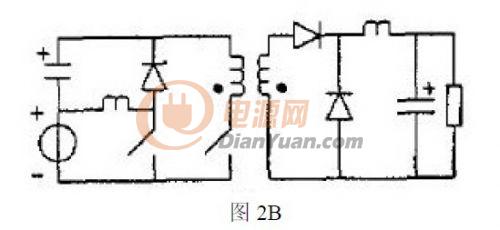
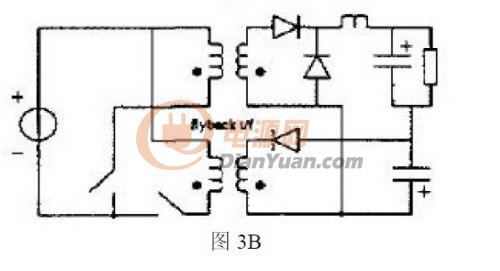
以上給出了一些基本拓?fù)涞腜FC 電路,,下面將具體分析圖1A 給出的電路。根據(jù)圖1A,,假設(shè)Buck-boost 和Buck 基本變換器都工作在CCM 狀態(tài)下,,本電路主要適用于中大功率的需求。
一.平均模型
假設(shè)電容電壓是常數(shù),,輸入電壓為整流過的正弦波,,如下所示

輸入Buck 基本變換器的電壓如下:

其中c V 是電容電壓, m ? 是載波頻率,。假設(shè)輸出校正良好,,穩(wěn)態(tài)時(shí),Buck 變換器的輸入電流如下:

其中,, 0 P 為PFC 電路的輸出功率,。根據(jù)以上計(jì)算與推導(dǎo),作出如圖4 所示的平均模型,,根據(jù)平均模型可知輸入電流為L(zhǎng) d i 1
和輸入Buck 變換器的電流之和,,其中1 d 是Buck-boost 變換器的占空比。

為了得到單位功率因數(shù),,可以得到以下等式:
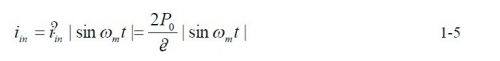
基于以上公式,, 利用MathCad 仿真幾個(gè)滾見參數(shù)波形。條件為
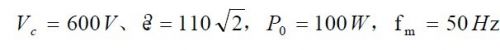
時(shí),,為了達(dá)到單位功率因素,,幾個(gè)主要電流、電壓的波形如圖5 所示:
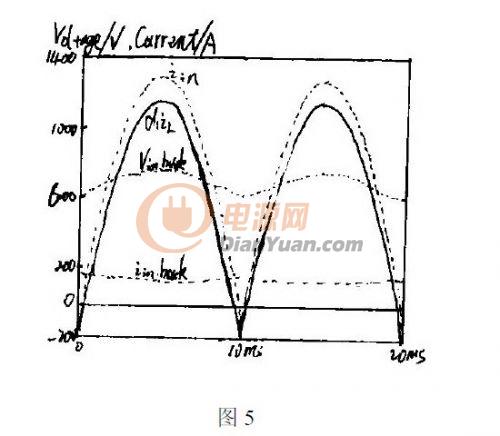
根據(jù)上圖所示,,為了達(dá)到單位功率因數(shù)的目的,,在一段時(shí)間內(nèi)L d i 1 為負(fù)值,所以可以使用一個(gè)允許能量雙向流通的開關(guān)來替代Buck-boost 中的二極管,。但實(shí)際上,,即使任然采用二極管,仍能保持很高的功率因數(shù),,略小于1.而且,,提高電容上的電壓值,可降
低in bock i . ,,從而保證功率因數(shù)一直維持在較高的水準(zhǔn)上,。
二.為了達(dá)到高功率因數(shù),兩個(gè)基本變換器分開控制,。標(biāo)記Buck-boost 變換器的占空比為
1 d ,,Buck 變換器的占空比為d2 ,,由此可以寫出 d 2的表達(dá)式:

其中U 為輸出直流電壓.由式1-3、1-4 推得:
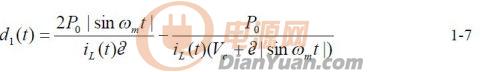
電感電流表達(dá)式如下:
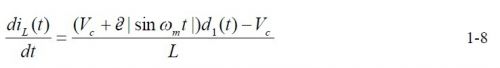
根據(jù)1-7,、1-8 有:
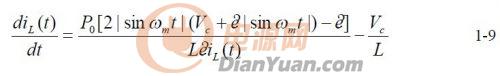
根據(jù)得出的1-9 式可以利用MathCad 的數(shù)值方法解出L i ,,如圖6 所示,再將L i 帶入式1-7,,可得出d1,。
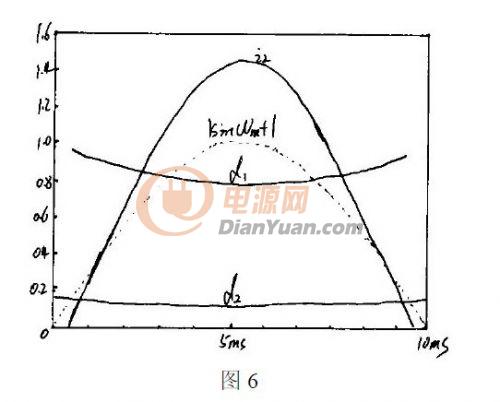
其中主電路波形接近過零點(diǎn)的附近, L i 無法求得數(shù)值解,。在實(shí)際的應(yīng)用上,,需要分開控制Buck-boost 變換器和Buck(Flyback 考慮隔離)變換器。
1 對(duì)于Flyback 變換器,,只需要簡(jiǎn)單的反饋控制環(huán),,但由于Flyback 變換器的輸入電壓為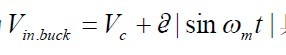
?具有較大的波動(dòng),所以講一個(gè)前饋環(huán)集合在反饋模型中,,有利于快速調(diào)整輸出,。
2 為了取得較高的功率因數(shù),前段的Buck-boost 變換器需由一個(gè)電流功率因數(shù)控制環(huán)來控制,,從而有效的使得輸入電流跟隨輸入電壓,。

