摘  要： 提出了一種基于Logistic和Henon混沌映射的圖像加密方法。首先利用Logistic混沌動力學系統(tǒng)產(chǎn)生的混沌序列,，通過動態(tài)量化算法增強其隨機性和復雜性,，對原始圖像進行混沌置亂，得到置亂圖像,。然后對Henon混沌映射產(chǎn)生的序列進行量化變換,，產(chǎn)生“異或”矩陣，與置亂后的圖像進行“異或”,，實現(xiàn)對圖像的加密,。仿真實驗表明，該方法具有良好的加密效果和較強的安全性,。
關鍵詞： 圖像加密,；混沌加密；Logistic映射,；Henon映射,；混沌映射

    數(shù)字圖像信息具有直觀,、形象,、易懂和信息量大等特點，已成為人們日常生活,、生產(chǎn)中接觸最多的信息種類之一[1],。隨著數(shù)字圖像在商業(yè)、軍事等不同程度的保密領域內的普及,，其安全性研究得到了廣泛的關注[2],。由于圖像存儲的特殊性，在傳統(tǒng)的密碼學領域并沒有單獨將圖像作為一種特殊的明文形式來考慮其加密特性,。雖然利用傳統(tǒng)的加密技術對圖像加密是可實現(xiàn)的,，但其加密效率低、安全性不高，不能適應圖像加密的需要,，因此專用的圖像加密技術被廣泛關注,。近年來混沌理論的應用研究引起了密碼學界的關注，由于混沌遍歷性正符合Shannon提出的密碼系統(tǒng)設計的擴散混淆等基本原則,，使混沌理論在圖像加密中得到廣泛應用[3-5],。本文提出一種基于Logistic和Henon雙混沌的圖像加密算法，并通過實驗分析證明,，該算法具有優(yōu)異的加密性能和運算效率,。
1 混沌理論及模型
    混沌與密碼學有著緊密的聯(lián)系，一個好的密碼系統(tǒng)應該具備以下幾個條件[6]：(1)把明文變換為盡可能隨機的密文,；(2)加密算法對明文有高度敏感性,；(3)加密系統(tǒng)對密鑰有高度敏感性。由于混沌具有對初值的敏感性,、良好的偽隨機特性,、軌道的不可預測性等特征，這些特征正好能夠滿足密碼系統(tǒng)的要求,。
Logistic映射是一個非常簡單卻具有重要意義的非線性迭代方程,，雖然它具有確定的方程形式，不包含任何不確定因素,，卻能產(chǎn)生完全隨機的,、對參數(shù)?滋的動態(tài)變化和初值極為敏感的序列。其定義如下：

初始值極度敏感,，對于相差的初始值,，方程迭代出來的軌跡差別相差很明顯，一般情況下,，很難從一段有限長度的序列來推斷出混沌系統(tǒng)的初始條件,。該混沌模型迭代方程簡單，混沌加密參數(shù)只有一個,，這決定了其加密運算速度快,，特別是比高維的混沌系統(tǒng)要快很多，但其密鑰空間比較小,，安全性稍差,，因此不考慮單獨使用它。
    Henon混沌系統(tǒng)是1976年由Henon提出的一種二維迭代系統(tǒng),，具有兩個參數(shù)的平面映射族,。Henon混沌映射定義如下：

式中，a,、b為控制參數(shù),，當1.05<a<1.8,、b=0.3時，Henon映射處于混沌狀態(tài)[7],。當處于混沌時,，它與Logistic模型同樣具有混沌的特性，不同的是Henon映射是一個具有兩個參數(shù)的平面映射族,。雖然理論上對Henon混沌的研究比較成熟,，但是由于其產(chǎn)生混沌序列的特殊性，一般也不單獨使用,。
2 加密解密矩陣的構造
    由于單混沌存在諸多缺陷,，密鑰空間小，且在有限精度的系統(tǒng)下受限制,，參考文獻[8]表明,，單混沌映射加密易受到攻擊利用。因此,，本文利用Logistic和Henon雙混沌系統(tǒng)來構造加密矩陣實現(xiàn)對圖像加密,。首先對Logistic混沌系統(tǒng)產(chǎn)生的序列通過一種動態(tài)量化得到置換矩陣的隨機數(shù)，對圖像的像素位置置亂,；再通過Henon混沌系統(tǒng)的映射,，利用整數(shù)求余的量化方法來得到“異或”加密的隨機數(shù)，與置亂后的圖像依次“異或”,。圖像加密效果完全取決于兩種混沌系統(tǒng)產(chǎn)生的隨機數(shù),，因此，對Logistic混沌的動態(tài)量化和Henon的整數(shù)求余量化成為實現(xiàn)加密效果的關鍵,。
    設原始圖像為I,，大小為m×n，則圖像I可以表示為：I=F(i,，j)(0≤i≤m,，0≤j≤n)。其中,，(i,，j)表示像素點位置，F(xiàn)(i,，j)表示該點處圖像的數(shù)據(jù),，則F(i，j)可構成圖像數(shù)據(jù)矩陣T,。
2.1 置換矩陣的構造
    首先利用一種隨機全排列生成算法來生成置換加密中所需的全排列。所謂全排列即是將M個不同元素按照一定的順序排列起來,，稱為這M個不同元素的一個全排列,。本置換方法分為行置換和列置換，行置換算法描述如下：
    (1)設生成的置換矩陣大小為m×n，首先要生成一個0~M-1之間的全排列元素,，元素數(shù)目為M(M>n),。
    (2)初始化全排列矩陣，令{0,，1,，…，M-1}中所有元素的一個全排列為{a0,，a1,，…，aM-1},，當i≠j時,，有ai≠aj。全排列初始值系數(shù)為L,，令n=?骔L×M」,，L可以當密鑰給出，一般L在(0.5,，0.7)區(qū)間即可,。若太小，則產(chǎn)生的全排列隨機性差,；若太大,，則數(shù)據(jù)重復多，將會增加系統(tǒng)的迭代次數(shù),。
    (3)設所用混沌系統(tǒng)方程為xn=f(xn-1),，本文用的是Logistic混沌模型，xn即為當前混沌序列,，每次都要進行迭代來產(chǎn)生新的混沌序列,。利用不等分區(qū)間的動態(tài)量化對混沌序列進行進一步處理，以增強其隨機性和復雜度,，本文利用參考文獻[9]的判決公式(3)對Logistic混沌方程式(1)產(chǎn)生的序列{xn}進行判決,，可以得到K=2n進

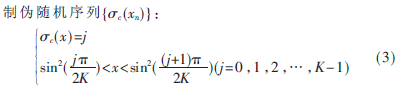
    定義序列{xn}經(jīng)過判決所在的位置構成序列為Pn={p1，p2,，…,，pn}，其中Pi=j,，即每一個xi都和一個xpi相對應,，可進行兩個位置元素交換，然后再重新判決,，通過這樣的量化即可得到n個0~M-1之間的隨機數(shù),。
    (4)初始化一個數(shù)組A,，初始為空，最大長度為m,，將步驟(2)生成的元素依次添加到A中,，若A中不存在生成的元素，則添加到A末尾,，否則舍棄,。直到A中元素為n個，然后將0~M-1間元素不在A中的依次添加到A中,，形成初始化全排列A,。
    (5)對初始化全排列A再進行一次全變換來增強隨機性，方法同步驟(2),，即將兩個對應位置元素A[Pi]同A[Ppi]的交換,。這里全變換的次數(shù)可以自行設定，但考慮系統(tǒng)運行的速度,，全變換輪數(shù)r不宜過大,，一般不超過5輪，由密鑰給出,。
    (6)反復執(zhí)行步驟(3),、(4)、(5)可得到一個m行隨機全排列,，即可構成m×n大小的行置換矩陣A′,。
    (7)行置換方法可看作函數(shù)B=E(A′，T),，其中B為加密后矩陣,，即是將T[i，j]的值賦給B[i,，Ppj],。列置換的方法和行置換方法相同，在此不再描述,。設矩陣B經(jīng)過列置換后為B′m×n,。
    該算法生成的全排列對混沌系統(tǒng)的初值敏感，密鑰的細微差別都將產(chǎn)生不同的全排列,。利用該算法可以生成任意多所需長度的隨機全排列,，算法中細微部分可以靈活處理，以增強密鑰強度,。
2.2 “異或”矩陣的構造
    利用Henon映射進行迭代產(chǎn)生隨機數(shù)構成“異或”矩陣,。由于Henon映射有一定的局限性，參考文獻[10]對常用的幾種混沌模型產(chǎn)生的序列進行隨機性測試,，得出Henon混沌映射的隨機性強度并不是十分理想,。因此,，本文用Henon混沌序列進行擾動變換后產(chǎn)生相關序列及參數(shù),，將輸出結果進行整數(shù)取余進一步量化得到“異或”矩陣,。其中部分細節(jié)可以靈活變換修改，在此不作詳細規(guī)定,。

    (4)反復執(zhí)行步驟(1),、(2)、(3),，直到構成大小為m×n的“異或”矩陣所需隨機數(shù),，設得到的“異或”矩陣為Cm×n。
     (5)將“異或”矩陣Cm×n與所得的置換矩陣B′m×n逐一“異或”即可得到加密矩陣,。
    “異或”矩陣的使用增強了整個算法的安全性,。置換矩陣和“異或”矩陣的使用，進一步增強了加密效果,，使抗攻擊能力得到增強,。
2.3 解密算法
    解密算法是加密算法的逆運算，在解密算法中,，置換矩陣是加密算法中置換矩陣的逆置換,，“異或”矩陣與加密中的“異或”矩陣相同，只是在解密過程中要先進行“異或”運算,，最后再進行“異或”運算,。
3 仿真實驗及測試分析
3.1 加密效果
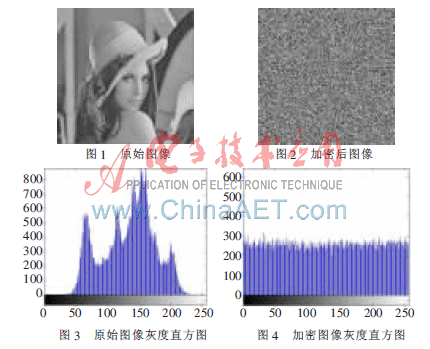
    本文采用大小為256×256、8 bit大小的Lena灰度圖像作為待測試圖像,。密鑰選取參數(shù)如下：x0=0.079 897 522 926 330 7,，μ0=4，r=1,，x′0=0.790 408 305 649 9,，y′0=0.210 030 319 169 164，t=3,，分別取小數(shù)點后3,、5、7位,。原始圖像及其灰度直方圖分別如圖1,、圖3所示，加密后的圖像和灰度直方圖分別如圖2,、圖4所示,。從圖中可以看出，加密后的圖像效果很好,，各像素的灰度值分布均勻,，與原始圖像完全不同,，對已知明文攻擊非常安全。

3.2 敏感性分析
    圖5為正確密鑰解密所得圖像,，通過比較可知,，與原圖的像素值完全相同，表明該算法沒有信息的丟失,。當密鑰中的x0=0.079 897 522 926 300 6,、其他密鑰參數(shù)不變時，解密所得圖像如圖6所示,?？梢娂词故褂门c正確密鑰差值微小錯誤的密鑰進行解密，得到的仍是與原圖像差別很大的錯誤圖像,，即說明本文所用算法對密鑰具有高度的敏感性,。

3.3 圖像剪裁測試
    從解密后的圖像中，剪裁掉右上角25%大小后的圖像如圖7所示,，剪裁掉中間一個大小為100×100后的圖像如圖9所示,。經(jīng)解密后的圖像分別如圖8、圖10所示,?？梢钥闯觯瑢γ芪倪M行剪裁干擾后進行恢復,，恢復后的圖像也能很清楚地反映原始圖像的一些特征,，而且密文集中剪裁出的點都分散到原圖像的不同位置，說明對圖像的加密效果比較理想,。

3.4 圖像相關性分析
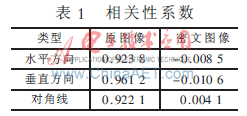
    為了分析原圖像與密文圖像的相鄰像素相關性,，在水平、垂直和對角線方向上分別從原始圖像和密文圖像中隨機選擇2 000對相鄰的像素點,，并按照參考文獻[10]中公式計算相關性,，圖11、圖12分別是圖像加密前后3個方向(水平方向,、垂直方向,、對角線方向)的相鄰像素相關性。

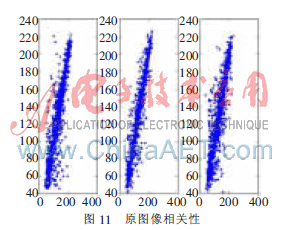
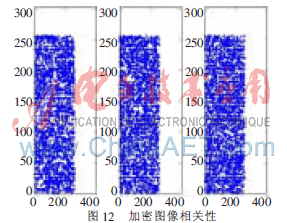
     表1為按3個方向計算所得的相關系數(shù)結果,。由結果可知,，原始明文圖像相鄰像素是高度相關的，相關系數(shù)接近于1,。而加密圖像的相鄰像素相關系數(shù)接近于0,，相鄰像素已基本不相關，說明明文的統(tǒng)計特征已被擴散到隨機的密文中。

    本文提出基于雙混沌映射的圖像加密方法,，充分利用混沌映射的性質實現(xiàn)圖像的加密,。相對于傳統(tǒng)的單一混沌映射，密鑰空間選擇更廣,，提高了密鑰流的線性復雜度,，很大程度上增強了圖像加密的效果。實驗及測試分析證明,，本方法簡單易行,、可靠性和安全性較好,。
參考文獻：
[1] JAIN A K.著.數(shù)字圖像處理基礎[M].韓博,，等譯.北京：清華大學出版社，2006.
[2] 廖曉峰.混沌密碼學原理及其應用[M].北京：科學出版社,，2009：232.
[3] MATTEWS R. On the derivation of a chaos encryptional algorithm[J]. Cryptologia,， 1989，13：29-42.
[4] 李國輝,，徐得名,，周世平.隨機性參數(shù)自適應的混沌同步[J].物理學報，2004,，53(2)：379-382.
[5] 曹美君,，張宏.混沌理論在數(shù)據(jù)加密中的應用[J].信息技術，2009(6)：169-171.
[6] 鐘華．基于混沌技術的圖像加密研究[D]．長沙：長沙理工大學,，2006.
[7] HENON M. A two-dimensional mapping with strange attractor[J]. Communication in Mathematical Physics,， 1978(50)：69-70.
[8] CHEN G， MAO Y. A symmetric image encryption scheme based on 3D chaotic cat maps[ J ]. Chaos,， Solitons and Fractals,， 2004(21)：749-761.
[9] 馮明庫，薛迎宵.混沌吸引子隨機性的一種判別方法[J].計算機工程與應用,，2007,，43(15)：56-58.
[10] 蔡覺平，李贊,，宋文濤．一種混沌偽隨機序列復雜度分析法[J].物理學報,，2003，52(8).