摘  要： 從數(shù)學(xué)上分析了弧矩在數(shù)字圖像縮放時(shí)的變化規(guī)律，得出通過(guò)組合矩的方法無(wú)法改善其縮放不變性的結(jié)論,，并指出了改善其縮放不變性的兩種方法,。仿真結(jié)果證明了本文所提出的結(jié)論的正確性和方法的可行性。
關(guān)鍵詞： Hu矩,；數(shù)字圖像,；縮放不變性；分辨率

    基于Hu矩在模擬圖像中具有圖像平移,、旋轉(zhuǎn),、縮放不變性的特點(diǎn)[1]，其作為識(shí)別的特征量已廣泛應(yīng)用于模式識(shí)別以及跟蹤等許多模擬圖像分析領(lǐng)域[2],。但Hu矩在數(shù)字圖像中并不具有縮放不變性,，不適合應(yīng)用于數(shù)字圖像分析[3]， 因此,，通過(guò)改造Hu矩使其能同時(shí)應(yīng)用于數(shù)/模圖像領(lǐng)域的分析,，成為許多研究人員的共同目標(biāo)[3-6]。
目前,，大部分對(duì)Hu矩的改造主要集中在組合矩方面[3-6],，但實(shí)際上組合矩的數(shù)學(xué)理論基礎(chǔ)存在一定的問(wèn)題，因?yàn)槠渌褂玫膞′=kx和y′=ky兩個(gè)公式在數(shù)字圖像縮放時(shí)并不成立,，因此,，使用這兩個(gè)公式推導(dǎo)出的組合矩并不能有效地改善數(shù)字圖像中Hu矩的縮放不變性。從數(shù)學(xué)角度推導(dǎo)出Hu矩在數(shù)字圖像縮放時(shí)的變化規(guī)律是找到改善其縮放不變性的基礎(chǔ),，這也是本文研究的重點(diǎn),。通過(guò)對(duì)其變化規(guī)律的研究，本文得出了兩種改善其縮放不變性的方法,。實(shí)驗(yàn)證實(shí)了這兩種方法的可行性,，同時(shí)顯示了Hu矩在識(shí)別系統(tǒng)中的應(yīng)用效果優(yōu)于Zemike[7]和krawtchouk[8]矩。
1 Hu矩簡(jiǎn)介
    設(shè)連續(xù)情況下二維圖像函數(shù)為f(x,，y),，則它的p+q階幾何矩和中心矩分別定義為：

    假設(shè)a=1，由圖1(a),、(c)可以看出,，在n/k為整數(shù),、m=0或m/k為整數(shù)時(shí)，ε的值隨著n,、m的增加而減少,。由圖1(a)、(b),、(d)可知，若n/k,、m/k為非整數(shù),，則ε變化比較不規(guī)律，ε值取決于n/k,、m/k的取整策略以及n,、m、k的大小,，同時(shí)由圖1(b),、(d)可知，如果同時(shí)按比例增大m,、n值,，可減少ε值。因?yàn)檎Ｇ闆r下,，m,、n、k為任意取值,，ε的變化很難找到規(guī)律,。因此，在不增大n的前提下,，通過(guò)矩不變量的組合(組合矩)來(lái)減少ε值的方式不具可行性,。因?yàn)榻M合矩只是通過(guò)Hu矩的組合來(lái)構(gòu)造新的不變量，而Hu矩在數(shù)字圖像縮放時(shí)的變化規(guī)律不一致,。因此減少ε值的方法只有兩種：一是在滿足一定分辨率的前提下使圖像縮放時(shí)圖像邊緣像素點(diǎn)的坐標(biāo)值與縮放系數(shù)的乘積為整數(shù),；二是使圖像的分辨率足夠高。
3 仿真分析
    對(duì)Hu矩在數(shù)字圖像縮放時(shí)的變化規(guī)律進(jìn)行分析,，在提出了使Hu矩對(duì)數(shù)字圖像縮放具有不變性的相關(guān)方法后,，利用Matlab軟件對(duì)本文方法的可行性進(jìn)行了仿真驗(yàn)證。圖2為用于Hu矩縮放不變性特性分析的四幅圖像,。圖3的曲線反映了圖2(a),、(b)、(c),、(d)四幅圖像在不同縮放系數(shù)下,，Hn(k)值的變化規(guī)律：鉆石實(shí)線反映了在條件1(較低像素下,，但n/k、m/k為整數(shù))時(shí)Hn(k)的值變化規(guī)律,，圖像原始分辨率為400×400,，圓虛線反映了在條件2(n/k為非整數(shù)時(shí)，圖像分辨率較低)時(shí)Hn(k)值的變化規(guī)律,，圖像原始分辨率為400×400,，方塊點(diǎn)虛線反映了在條件3(n/k為非整數(shù)但圖像具有較高的分辨率)時(shí)Hn(k)值的變化規(guī)律，圖像原始分辨率為1 200×1 200,。Hn(k)=0.4n+(Mn(k)-Mn(k=1))/Mn(k=1),，其中，k是縮放系數(shù),，Mn是Hu矩不變量,。仿真結(jié)果顯示，鉆石實(shí)線的波動(dòng)最小,，因此條件1下Hu矩具有最好的不變性,。但是現(xiàn)實(shí)的縮放很難達(dá)到條件1的要求，方塊虛線顯示提高分辨率可以很好地改善Hu矩的縮放不變性,。同時(shí)本文也具體對(duì)圖像的分辨率與識(shí)別率的關(guān)系進(jìn)行了分析,，圖4顯示了字母G的識(shí)別率與分辨率的關(guān)系，識(shí)別分別基于Hu矩,、Z矩,、K矩不變量，不變量之間的歐氏距離作為識(shí)別時(shí)的分類依據(jù)[9],。圖4顯示分辨率越高,，識(shí)別率越高，而且Hu矩具有最好的識(shí)別效果,。

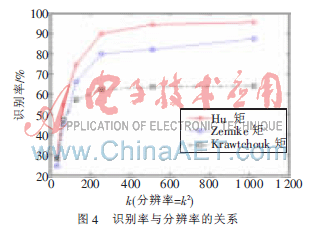
    本文提出了兩種使Hu矩在數(shù)字圖像縮放時(shí)具有不變性的方法,，仿真結(jié)果證明了本方法的可行性。同時(shí)仿真也顯示在較高像素條件下,，Hu矩具有比Z,、K矩更優(yōu)的應(yīng)用效果，因此,，Hu矩非常適合應(yīng)用于具有高圖像分辨率的數(shù)字圖像識(shí)別系統(tǒng),。
參考文獻(xiàn)
[1] HU M K. Visual pattern recognition by moment invariants[J].IRE Transactions on Information Theory， 1962,， 8(2)： 179-187.
[2] MERCIMEK M,， GULEZ K， MUMCU T V. Real object recognition using moment invariants[J]. Sadhana-Academy Proceedings in Engineering Sciences,， 2005,， 30(6)： 765-775.
[3] LIU J,， LIU Y C， YAN C X. Feature extraction technique based on the perceptive invariability[C]. Fifth International Conference on Fuzzy Systems and Knowledge Discovery,， 2008： 551-554.
[4] 徐學(xué)強(qiáng),，汪渤，賀鵬.統(tǒng)一Hu矩及在電視圖像目標(biāo)識(shí)別中的應(yīng)用[J].計(jì)算機(jī)工程與應(yīng)用,，2006,，42(29)：213-215.
[5] 杜亞娟，潘泉,，張洪才.一種新的不變矩特征在圖像識(shí)別中的應(yīng)用[J].系統(tǒng)工程與電子技術(shù),，1999，21(10)：71-74.
[6] 邵澤明,，朱劍英.RSTC不變矩圖像特征點(diǎn)匹配新方法[J].華南理工大學(xué)學(xué)報(bào)(自然科學(xué)版)，2008,，36(8)：37-40.
[7] SHUTLER J D,， NIXON M S. Zernike velocity moments for description and recognition of moving shapes[J]. Image and Vision Computer， 2001,， 24(4)： 343-356.
[8] ZHANG L,， XIAO W W， JI Z. Local affine transform invariant image watermarking by Krawtchouk moment invariants[J]. IET Information Security,， 2007,， 1(3)： 95-107.
[9] POTOCNIK B. Assessment of region-based noment invariants for object recognition[C]. 48th International Symposium ELMAR-2006 on Multimedia Signal Processing and Communications， 2006： 27-32.