摘 要: 討論了主目標距離與干擾目標截面積之間的關系,結合工程實際應用,建立了干擾目標與主目標截面積比值,即主目標距離的數(shù)學模型。解決了主目標在不同距離時干擾程度的問題,并進行了仿真實驗與結果分析。
關鍵詞: 地面探測雷達;CFAR;遮擋;干擾模型
噪聲與雜波是雷達工作的固有環(huán)境,地面探測雷達要求在復雜的雜波與噪聲背景下,保持恒定的虛警概率完成對動目標的自動檢測,現(xiàn)代動目標檢測(MTD)雷達大部分都采用參考單元(距離維)、恒虛警率(CFAR)處理技術來實現(xiàn)[1-2]。在大多數(shù)的應用場合下,由于CFAR在參考單元滑窗統(tǒng)計噪聲時不可避免地存在雜波邊緣與多目標干擾,尤其是近距離目標干擾,從而導致CFAR性能嚴重下降,甚至主目標被“遮擋”。
目前已經(jīng)有大量文獻[3-4]對CFAR技術在多(大)目標干擾環(huán)境下的檢測性能進行了分析,并且得出CFAR技術在多目標環(huán)境中檢測性能變差的結論;也有文獻[5]對當CFAR技術失效時的干擾程度進行了一定的研究,但該文獻[5]涉及的是一種理想狀態(tài),是基于各參考單元干擾目標的回波幅度一致的基礎上進行的討論,沒有考慮因距離不同而引起的干擾強度的差異,因此只適用于主目標處于較遠距離時刻。
本文就CA-CFAR和最小選擇(SO)CFAR兩種經(jīng)典處理方法,結合實際工程應用,對目標干擾模型進行了數(shù)學推導與建模。給出了在雷達探測范圍內,主目標被“遮擋”時干擾目標有效反射面積與距離之間的函數(shù)關系式,并對該數(shù)學推導模型進行了仿真驗證。
1 CFAR技術介紹
CFAR檢測器的結構框圖如圖1所示。輸入的數(shù)據(jù)通過相參積累(FIR或FFT)處理后,為了減少系統(tǒng)損失提高多目標的發(fā)現(xiàn)概率,通常對各頻道號信號分別做CFAR處理,圖1描述的就是某一頻道號進行濾波的結構框圖。為了防止主目標信號泄露,通常在主目標前后相鄰參考單元不參與噪聲估計,圖中Z1與Z2分別為主目標的前后m個單元的雜波噪聲平均值,函數(shù)f(Z1、Z2)是對Z1、Z2進行進一步處理(求平均或選大或選小等),完成雜波噪聲估值。
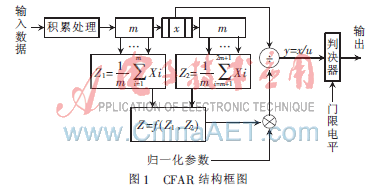

本文主要討論主目標被其他大目標“遮擋”的問題,越靠近雷達的目標對主目標干擾程度越嚴重。所以主目標的前沿參考窗影響更為嚴重,而且參考單元中第一個參考單元的干擾目標影響最大,特別是在近距離處,雷達回波的信噪比很高,并且常常采用STC(靈敏度時間控制)來滿足A/D采樣動態(tài)以及收發(fā)機的動態(tài)要求,這樣近距離噪聲將非常小。因此為了簡化計算以及便于仿真,故選擇干擾最嚴重的情況進行討論,即假設某相同頻道號的干擾目標都集中在最靠近雷達的參考單元內,并且假設參考單元內的噪聲與D比值為零,則式(5)可簡化為:

3 計算機仿真實驗與分析
針對數(shù)學模型進行計算機仿真試驗及分析,由于該數(shù)學模型是基于地面探測雷達工程實現(xiàn)過程推導,因此在仿真試驗中對某些參數(shù)做如下假設:雜波和噪聲的幅度為瑞利分布,雷達動目標檢測的虛警概率Pfas=10-6,脈沖寬度為0.2 μs,參考單元數(shù)m依次取值為8、16和32三種參數(shù),近距離盲區(qū)參數(shù)k取5。
圖2所示為基于CA-CFAR處理方法的干擾模型,Δδ為干擾目標與主目標的截面積比值,R為主目標所處距離。當主目標在某一距離時,干擾目標比主目標至少大多少時可能“遮擋”主目標。圖中目標的干擾情況在近距離表現(xiàn)得更為復雜,剛開始干擾目標要比主目標大很多(m=32時,Δδ大約為20 dB)才可能導致主目標被“遮擋”。隨著距離的增加,兩者截面積比值?駐?滓曲線也在不斷下降,此時主目標變得很容易被“遮擋”(m=32時,Δδ最小將近-25 dB)。由于該距離段比較短,當距離達到150(m+k+1)τ時,干擾程度逐漸減弱,截面積比值Δδ曲線快速上升。圖中可以看出,在近距離干擾最嚴重的距離段,一個小目標就可能導致雷達“漏警”。
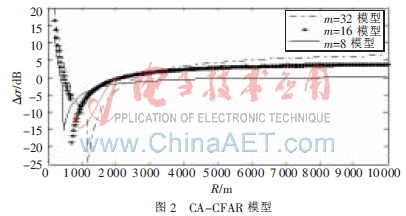
圖3所示為SO-CFAR處理模型時截面積比值Δδ與距離R的關系曲線圖,從圖中可以看出,隨著距離增加,曲線呈下降趨勢,到幾公里后曲線趨于穩(wěn)定,此時由于距離的差異而產(chǎn)生的的影響不大。
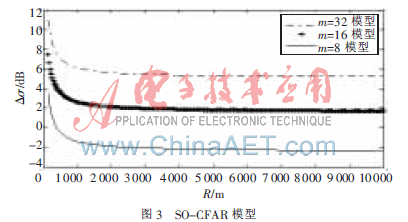
由圖2、圖3可以看出SO-CFAR模型比CA-CFAR模型的抗干擾能力更強(特別是近距離),這也與眾多的文獻[7]研究結果相同。參考單元較多時,對于噪聲功率估計更穩(wěn)定,而且抗干擾能力較強,但是所涉及的距離越長越可能引入更多的干擾目標,同時參考單元越多所涉及的硬件開銷越大。因此在工程應用中要綜合考慮參考單元的數(shù)目。圖2中也容易看出CA-CFAR處理方法,主目標在2 km以內很容易被干擾目標“遮擋”,由于式(2)中回波功率正比于目標有效截面積(Pr∝δ),因此可參考圖2曲線,在原有的STC電路上,精心設計其控制曲線來降低近距離目標被干擾的可能性,提高目標的發(fā)現(xiàn)概率。
本文不僅從理論上,更側重的是從工程實現(xiàn)的角度對問題進行建模、分析,結合CA-CFAR與SO-CFAR處理技術,針對地面探測脈沖雷達進行研究,分析了目標距離與干擾目標之間的關系,并且進行仿真實驗及結果分析,對從事雷達總體設計以及信號處理的研究起到一定的借鑒意義,也為雷達整機野外調試實驗起到一些指導作用。
參考文獻
[1] 劉敬興.地面探測脈沖壓縮雷達的動目標檢測[J].電子技術應用,2010,36(1):132-135.
[2] 馬曉巖,向家彬.雷達信號處理[M].長沙:湖南科學技術出版社,1998.
[3] MASHADEM B.M-sweeps detection analysis of cell-averaging CFAR processors in multiple-target situations[J].IEE proc.-F, 1994, 141(2): 103-108.
[4] HUSSAINI E K, MASHADE M B.Performance of cell-averaging CFAR and order-statisticsdetectors processing correlated sweeps for multiple interfering targets[J]. Signal Processing, 1996, 49(1):111-118.
[5] 杜朋飛,張祥軍.單元平均恒虛警率檢測中的一個新結論[J].現(xiàn)代雷達,2007,29(2):60-62.
[6] 郭仕劍,王寶順.MATLAB7.X數(shù)字信號處理[M].北京:人民郵電出版社,2006.
[7] 陳那.信號測試、處理與系統(tǒng)控制分析技術使用全書[M].北京:清華大學出版社,2005.

