摘  要： 針對T-S模型的有記憶非易碎模糊系統(tǒng),，基于Lyapunov穩(wěn)定性理論，利用線性矩陣不等式(LMI)方法,，借助Schur補(bǔ)引理,，討論了該模糊系統(tǒng)的H∞狀態(tài)反饋控制器的設(shè)計(jì)問題。在控制器增益為加法式攝動(dòng)的有界條件下,，得到了基于T-S模型的有記憶非易碎模糊系統(tǒng),，滿足了H∞性能指標(biāo)的一個(gè)充分條件,，仿真結(jié)果表明了設(shè)計(jì)方法的有效性。  
關(guān)鍵詞： 增益攝動(dòng),；有記憶,；非易碎控制；H∞控制

　H∞控制理論于20世紀(jì)80年代初由Zames[1]首次提出,，即運(yùn)用小增益定理,，設(shè)計(jì)狀態(tài)反饋控制器，該控制器在參數(shù)不確定和有界擾動(dòng)的雙重影響下,，閉環(huán)系統(tǒng)仍能保持穩(wěn)定,。H∞控制理論一經(jīng)提出，很多學(xué)者即投入研究[2-3],，但均未考慮控制器增益的不確定性(易碎性),。易碎性會造成閉環(huán)系統(tǒng)的性能下降，破壞系統(tǒng)的穩(wěn)定,，因而考慮系統(tǒng)的非易碎H∞控制必不可少,。近年來，非易碎控制問題的研究有了一定成果[4-6],，參考文獻(xiàn)[4]通過LMI方法,，設(shè)計(jì)了滿足H∞性能指標(biāo)的T-S模糊非易碎控制器；參考文獻(xiàn)[5]通過Lyapunov函數(shù)的穩(wěn)定分析理論及分散控制理論,，設(shè)計(jì)了大規(guī)模的模糊系統(tǒng)在信息交互時(shí)的魯棒非易碎H∞控制器,；參考文獻(xiàn)[6]研究了參數(shù)不確定的T-S模糊中立模型的非易碎H∞控制。對于有記憶控制有一定的研究：參考文獻(xiàn)[7]對線性時(shí)滯系統(tǒng)進(jìn)行了有記憶的H∞控制,，但未考慮非線性系統(tǒng)和非易碎系統(tǒng),；參考文獻(xiàn)[8]對非線性系統(tǒng)進(jìn)行了有記憶的H∞控制，但未使用T-S模糊系統(tǒng),，同樣未考慮非易碎系統(tǒng)。綜上所述,，以上的文獻(xiàn)均未對記憶性系統(tǒng),、非易碎系統(tǒng)、T-S模糊系統(tǒng)及H∞控制同時(shí)進(jìn)行研究,。因此本文對基于T-S模型的有記憶非易碎模糊系統(tǒng)的H∞控制進(jìn)行研究,。
1 問題描述
　一類有記憶非易碎T-S模糊系統(tǒng)：





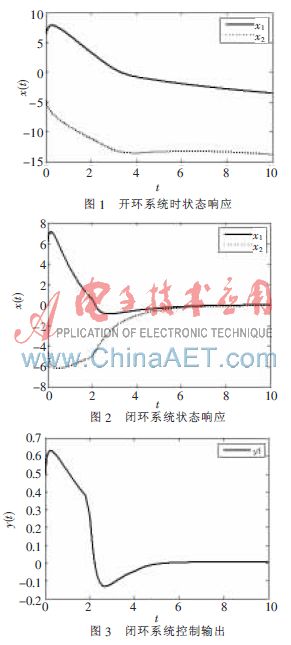
　由Simulink得到算例系統(tǒng)的開環(huán)狀態(tài)響應(yīng)曲線，如圖1所示,。加入控制率后,，閉環(huán)系統(tǒng)的曲線如圖2~圖3所示?？梢钥闯?，系統(tǒng)在有記憶非易碎控制器作用下是漸近穩(wěn)定的,。

　本文以基于T-S模型的有記憶非易碎模糊系統(tǒng)為對象，討論了該模糊系統(tǒng)在H∞控制問題中控制器的設(shè)計(jì),。采用線性矩陣不等式(LMI)的處理方法,，導(dǎo)出了H∞狀態(tài)反饋控制器存在的充分條件。所設(shè)計(jì)的狀態(tài)反饋控制器能保證閉環(huán)系統(tǒng)漸近穩(wěn)定并滿足設(shè)定的H∞控制指標(biāo),。并用數(shù)值算例驗(yàn)證了結(jié)論的有效性,。
參考文獻(xiàn)
[1] ZAMES G. Feedback and optimal sensitivity： model reference transfer functions， multiplicative semi-norms,， and approximate inverses[J]. IEEE Trans Automt Control,， 1981(2)： 301-320.
[2] KHARGONEKAR P P， PETERSEN I R,， ZHOU K. Robust stabilization of uncertain linear systems： quadratic stabilizability and H∞ control theory[J]. IEEE Transactions on Automatic Control,， 1990(3)： 356-361.
[3] SCHAFT V A J. L2-gain analysis of nonlinear systems and nonlinear state-feedback H∞ control[J]. IEEE Transactions on Automatic Control， 1992(6)： 770-784.
[4] 岳菊梅,，李俊民.不確定T-S模糊系統(tǒng)魯棒非脆弱H∞控制[J].系統(tǒng)工程與電子技術(shù),，2008(5)：909-913.
[5] Liu Xinrui， Zhang Huaguang,， Liu Guowei. Robust and non-fragile H∞ control for affine fuzzy large-scale systems[J]. Intelligent Control and Automation,， 2008(27)： 6107-6112.
[6] Yang Jun， Zhong Shouming,， Xiong Lianglin. A descriptor system approach to non-fragile H∞ control for uncertain fuzzy neutral systems[J]. Fuzzy Sets and Systems,， 2009(4)：423-438.
[7] 姜偕富，費(fèi)樹岷,，馮純伯,，線性時(shí)滯系統(tǒng)的記憶與無記憶復(fù)合H∞狀態(tài)反饋控制[J].系統(tǒng)工程理論與實(shí)踐，2002(6)：21-25.
[8] 王巖青,，趙金華,，姜長生.一類非線性不確定時(shí)滯系統(tǒng)的記憶與無記憶復(fù)合H∞狀態(tài)反饋控制[J].電光與控制，2006(2)：35-37.
[9] Xu Shengyuan,， LAM J,， Wang Jianliang， et al. Non-fragile positive real control for uncertain linear neutral delay systems[J]. Systems&Control Lett,， 2004(52)：59-74.