FFT(快速傅里葉變換)在無線通信、語音識別,、圖像處理和頻譜分析等領(lǐng)域有著廣泛應(yīng)用,。在FFT運算中，核心操作是蝶形運算,，而蝶形運算的主要操作是向量旋轉(zhuǎn),，實現(xiàn)向量旋轉(zhuǎn)可用復數(shù)乘法運算來實現(xiàn)，但復數(shù)乘耗費了FFT運算中大量的乘法器資源,。CORDIC算法只需簡單的移位與加減運算就能實現(xiàn)向量旋轉(zhuǎn),，具有使用資源少、硬件規(guī)模小等優(yōu)勢,。因此在FFT蝶形運算中用其代替?zhèn)鹘y(tǒng)FFT運算中的復數(shù)乘法器,，可以獲得更好的性能。但傳統(tǒng)CORDIC算法中每次CORDIC迭代方向需由剩余角度的計算來確定,，影響了工作速度,。為此，本文根據(jù)定點FFT復乘中旋轉(zhuǎn)因子的旋轉(zhuǎn)方向可預先確定的特點,，對CORDIC算法做了一些改進,，在節(jié)省資源的同時保證了工作速度。
1 CORDIC算法原理
    假設(shè)直角坐標系中有一向量A(Xa,，Ya),，逆時針旋轉(zhuǎn)?茲角度后得到另一個向量B(Xb,，Yb)，這個過程可用如下矩陣表示：
  
 

    針對這一特點,，可在CORDIC算法上做一點改進,，把旋轉(zhuǎn)因子所對應(yīng)的CORDIC旋轉(zhuǎn)系數(shù)預先存在ROM中（人工計算旋轉(zhuǎn)系數(shù)比較麻煩，可用MATLAB編一段程序來計算,，并把旋轉(zhuǎn)系數(shù)存為.mif文件以便ROM初始化）,，而不是把旋轉(zhuǎn)因子角度預先存在ROM中。這樣,，在進行CORDIC運算時,，直接從ROM中取出旋轉(zhuǎn)系數(shù)，從而減少計算Zi來確定下一步旋轉(zhuǎn)方向的步驟,，減少CORDIC模塊設(shè)計的復雜性,，提高了運算速度，并且旋轉(zhuǎn)系數(shù)不比旋轉(zhuǎn)因子角度占用的ROM資源多,。另外由于旋轉(zhuǎn)因子需要進行0°,、-90°或+90°三種預旋轉(zhuǎn)，所以預旋轉(zhuǎn)還要分配兩位二進制數(shù),，這樣存儲旋轉(zhuǎn)系數(shù)的ROM就為18位的ROM,。
    改進的CORDIC算法結(jié)構(gòu)如圖1所示，所有旋轉(zhuǎn)因子所對應(yīng)的CORDIC旋轉(zhuǎn)系數(shù)都存儲在ROM中,，通過地址產(chǎn)生器的控制實現(xiàn)序列與相應(yīng)的旋轉(zhuǎn)因子的復乘運算,。與傳統(tǒng)CORDIC算法相比去掉了預旋轉(zhuǎn)角與已旋轉(zhuǎn)角之差的計算來確定下一次旋轉(zhuǎn)方向的結(jié)構(gòu)，不但增加了系數(shù)寄存器模塊,，而且總體上結(jié)構(gòu)更為簡單,。此CORDIC算法還采用流水線結(jié)構(gòu)提高了運算的速度，從當前VLSI的發(fā)展趨勢上來看,，芯片內(nèi)的門資源相對富裕,，對流水線CORDIC的實現(xiàn)規(guī)模約束很小。此外,，流水線CORDIC不存在迭代式CORDIC的反饋回路,，使得單元結(jié)構(gòu)更加規(guī)則，有利于VLSI實現(xiàn),。

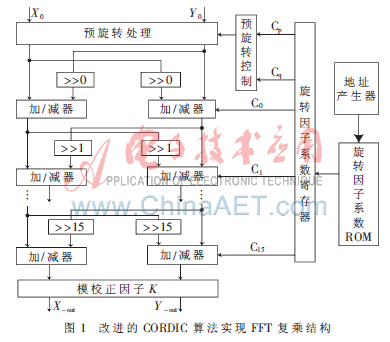
3.3 模校正因子的實現(xiàn)
    基本CORDIC算法中在n級迭代執(zhí)行之后,，被旋轉(zhuǎn)向量的模已經(jīng)被改變了，算法的完全實現(xiàn)應(yīng)該附加一個模校正環(huán)節(jié),，即Xn,、Yn乘以模校正因子。對于迭代次數(shù)N大于10的CORDIC算法,，其模校正因子可認為已趨近常數(shù)K=0.607 25,。而直接在流水結(jié)構(gòu)后附加乘法器的直接實現(xiàn)方法,，使原本由移位器和加法器組成的整體結(jié)構(gòu)變得不規(guī)則，同時乘法器一級速度的變慢會降低整個流水的吞吐率[3,，4],。

這樣分解后，被旋轉(zhuǎn)向量與K的乘轉(zhuǎn)化為簡單的移位加減運算,，從而可以解決乘法器一級速度變慢而降低整個流水線吞吐率的問題,。其硬件實現(xiàn)結(jié)構(gòu)如圖2所示。這種結(jié)構(gòu)進一步降低了硬件復雜度,，與前面的流水線CORDIC結(jié)構(gòu)相似,，使整體結(jié)構(gòu)更加規(guī)則統(tǒng)一，有利于VLSI實現(xiàn),。

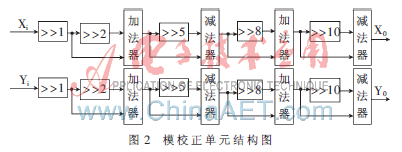
4 FFT復乘的FPGA實現(xiàn)
    由于軟件和DSP實現(xiàn)的速度較慢,，而FPGA資源豐富，組織結(jié)構(gòu)便于采用流水線結(jié)構(gòu)和并行運算,，其速度快,、擴展能力強，所以CORDIC算法的移位,、加減法運算和流水線結(jié)構(gòu)更容易在FPGA上實現(xiàn),。本文在Altera公司的QuartusⅡ7.2軟件環(huán)境下使用VHDL，利用上述各種算法設(shè)計了16 bit寬的FFT復乘模塊并在CycloneⅡ EP2C35F672C6芯片上進行驗證,。
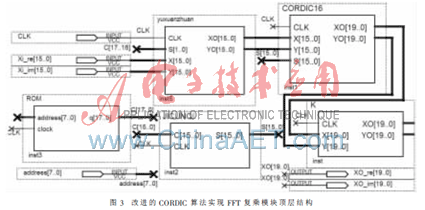
    圖3為改進的16級流水線結(jié)構(gòu)的CORDIC算法實現(xiàn)復乘模塊的頂層結(jié)構(gòu)圖，address為ROM的地址,，Xi_re,、Xi_im為輸入序列的實部和虛部，Xo_re,、Xo_im為旋轉(zhuǎn)后的實部和虛部,。輸入數(shù)據(jù)為16 bit寬，為提高精度,，對所有內(nèi)部信號及輸出信號都用20 bit的補碼,。整個復乘主要由系數(shù)ROM、預旋轉(zhuǎn),、16級流水線CORDIC迭代,、系數(shù)寄存器和模校正因子K 5個模塊組成。

    小,，但不能完全消除,。

    圖5為改進的CORDIC算法實現(xiàn)FFT復乘資源消耗與最高工作速度情況。傳統(tǒng)的復乘要4個乘法器,，所以傳統(tǒng)的復乘要實現(xiàn)16 bit位寬復乘需用此芯片中的8個9 bit乘法單元,，而從資源消耗情況來看,，改進的CORDIC算法實現(xiàn)此復乘沒有用乘法器，整個邏輯單元消耗也只有4%,；另外基于改進的CORDIC算法的復乘最高工作頻率達到了190 MHz,，與傳統(tǒng)CORDIC算法的復乘速度（約130 MHz）相比有較大提高，在節(jié)約資源的同時提高了工作速度,。

    本文利用定點FFT復乘運算中旋轉(zhuǎn)因子的旋轉(zhuǎn)系數(shù)可預先求出的特點,，采用改進流水線結(jié)構(gòu)的CORDIC算法，與傳統(tǒng)的CORDIC算法的復乘相比,，不僅不需要乘法器實現(xiàn)了FFT運算中序列與旋轉(zhuǎn)因子的復數(shù)乘運算,，并且在節(jié)約資源的同時提升了工作速度。這種基于改進的CORDIC算法的復乘運算對提高FFT處理器的速度和減少資源消耗有較大意義,。同時,，利用VHDL語言，采用模塊化設(shè)計思想,，使得本設(shè)計可移植性強,、通用性好，只需作少量改動（如增加位寬,，增加迭代次數(shù)）,，便可滿足精度上的更高要求，具有一定的工程實際意義和應(yīng)用前景,。
參考文獻
[1] 李成詩,，初建朋.基于CORDIC的一種高速實時定點FFT的FPGA實現(xiàn)[J].微電子學與計算機，2004,，21(4).
[2] 吳偉,，唐斌.現(xiàn)代雷達中的高速FFT設(shè)計[J].空軍工程大學學報（自然科學版），2005(10).
[3] KHARRAT M W,，LOULOU M,，MASMOUDI N，et al.A new method to implement CORDIC algorithm[C].IEEE International Conference on Electronic,，Circuit and Systems,，2001(2)：715-718.
[4] 楊宇，毛志剛,，來逢昌.一種改進的流水線CORDIC算法結(jié)構(gòu)[J].微處理機,，2006(8).
[5] 李滔.流水線CORDIC算法及其應(yīng)用研究[D].北京理工大學，1999.