摘 要： 針對EZW和SPIHT算法在壓縮效率和壓縮性能方面的不足,，提出了改進算法,，將(5,3)整數(shù)小波變化與這兩種算法結(jié)合起來,并對三個子帶分別進行編碼,，給出了兩種算法的峰值信噪比、均方誤差的理論對比分析,。所有結(jié)論被 Matlab仿真試驗驗證,。
關鍵詞： 整數(shù)小波變化; 峰值信噪比; 均方誤差; 均方根誤差; EZW; SPIHT
隨著多媒體和通信技術的發(fā)展，人們對通信速度,、數(shù)據(jù)的處理能力提出了近乎苛刻的要求,。近年來針對圖像壓縮而提出的算法，既要能夠有效地去除空間冗余,、視覺冗余,、時間冗余等各方面的冗余信息，還需充分考慮其壓縮效率和解壓縮效率,，圖像的失真度等各方面的因素,。
基于小波變換的圖像編碼技術主要是利用圖像經(jīng)過小波變換后的系數(shù)分布特點而得到不同的編碼方案。EZW（嵌入式零樹編碼）和SPIHT（分層樹集分割編碼）是兩種常見的基于小波變換的嵌入式零樹編碼方案,。這兩種編碼方法不但實現(xiàn)了壓縮比可調(diào),、分辨率可調(diào)，且壓縮后的圖像有很好的信噪比,。因此現(xiàn)在很多圖像壓縮標準都采用了這兩種編碼方法,。
實驗表明，EZW和SPIHT對三個子帶取相同的熵值進行編碼并沒有充分表現(xiàn)出經(jīng)過小波變換后圖像子帶間的相關性,。同時SPIHT算法在實現(xiàn)上需要維護三個動態(tài)鏈表,，占用大量的內(nèi)存，不利于算法的實現(xiàn)和推廣,?；谝陨蟽煞矫娴娜毕荩疚奶岢隽烁倪M算法,。
1 算法簡介及實現(xiàn)
1.1 整數(shù)小波變化
研究圖像壓縮的編碼方法,，首先要選擇合適的量化方案，將圖像的空間域信息轉(zhuǎn)換為頻域信息,?；谔嵘惴ǖ恼麛?shù)小波變化，它既可以在多分辨率級上對圖像進行分析,，又不涉及浮點數(shù)的運算,，不但簡化了計算量,還可以用于無損壓縮。其主要步驟如下：
(1)分裂：將圖像Sj=(ej-1,oj-1)分解為一個偶數(shù)序列和一個奇數(shù)序列,；
(2)預測：利用偶數(shù)序列去預測奇數(shù)序列,，得到高頻系數(shù),，dj-1=oj-1-P(ej-1)，對應圖像的細節(jié)系數(shù),；
(3)更新：預測后的圖像可能出現(xiàn)某些特征系數(shù)與原圖像并不一致,，此時就需要更新操作Sj-1=ej-1+U(dj-1)。
整個提升方案都是可逆的,。
由提升方案構(gòu)造的（5,3）整數(shù)小波變換構(gòu)造了雙正交緊支小波基,，它既可以用于無損圖像壓縮，也可以用于有損圖像壓縮,。因此本文選擇（5,，3）整數(shù)小波變換作為圖像的量化方案。 其算法實現(xiàn)過程如下：
圖1為lena經(jīng)過三層(5,3)整數(shù)小波分解后的圖像,。
1.2 EZW算法
經(jīng)過小波變換后的圖像分別在水平方向,、垂直方向和對角方向連接,，形成四叉樹結(jié)構(gòu),，如圖2所示(Z字型為其掃描順序)。
具體步驟如下：
(2)進行主掃描,，比較小波系數(shù)和T值的大小,，依次輸出下列編碼流，如圖3所示,；
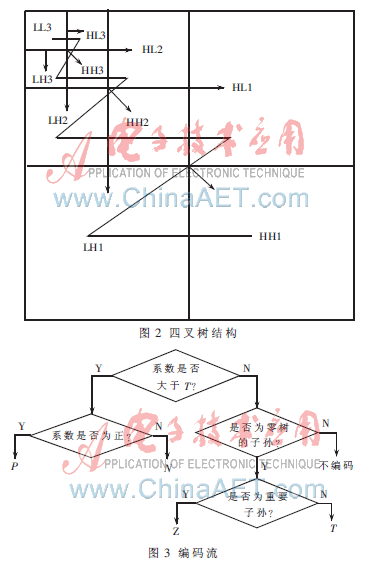
(3)進行輔掃描,，就是對系數(shù)P或N進行量化編碼。
每次掃描結(jié)束后只需將T（熵值）,、scancode（主掃描表）,、flaglist（輔掃描表）進行傳輸，EZW就是采用這種逐次逼近的嵌入式編碼方式,。
1.3 SPIHT算法
SPIHT算法采用了與EZW算法相似的零樹結(jié)構(gòu),，它定義了三個動態(tài)鏈表LIS（無效集表）、LIP（無效像素集表）和LSP（有效像素表）,。其中LIP和LSP中存儲的是節(jié)點坐標,，LIS中存儲的是坐標集,其類型有L型和D型,L表示非直系親屬,D表示直系親屬。具體算法過程如下：
else output=0 add (k,l) to LIP
③如果LIS的類型為L
if Sn(L(i,j))==1(each (k,l)∈O(i,j))
output=1 and add (k,l)D to LIS
else output=0
2 EZW和SPIHT算法的優(yōu)缺點
2.1 EZW 算法的優(yōu)點
(1)利用經(jīng)過小波變化后圖像大部分能量集中在低頻部分這一特點,，進行有效的零樹編碼,；
(2)采用了SAQ（逐次量化逼近）的方法選擇熵值，這樣不但使壓縮后的圖像有很好的信噪比,，而且也很好地利用了帶寬,，在傳輸圖像的過程中首先接收到的是圖像的輪廓部分，如果接收者認為不需要這幅圖像可以中斷圖像的傳輸,；
(3)經(jīng)過EZW編碼后的圖像,，實現(xiàn)了分辨率可調(diào),、信噪比可調(diào)、壓縮比可調(diào),；
(4)使用自適應算法還可以使EZW算法應用于無損壓縮,。
2.2 SPIHT算法的優(yōu)點
SPIHT算法不僅繼承了EZW算法的所有優(yōu)點，還有如下優(yōu)勢：
(1)采用了比EZW算法更細致的嵌入式比特流,，使壓縮后圖像的信噪比更高,；
(2)每次只需要輸出1 bit的信息流,在解碼過程中不需要對信息流重新排列。
2.3 EZW算法和SPIHT算法的缺點
(1)經(jīng)過小波變換后圖像的LL部分反映了圖像的輪廓信息,，聚集了壓縮后圖像的絕大部分能量,，人眼對該部分的信息也較為敏感。EZW算法和SPIHT算法沒有考慮到LL部分的重要性,，使其解碼后失真度較大,。
(2)經(jīng)過小波變換后,圖像在LH部分很好地保留了
垂直分界線,在HL部分很好地保留了水平分界線，EZW算法和SPIHT算法只考慮了子帶間的相關,，沒有考慮子帶內(nèi)的相關性,，對三者取相同的熵值進行編碼，造成了壓縮后圖像的邊界拓延性差,。
(3)在EZW算法中,，如果一棵樹的根節(jié)點是重要的，但是它所有的子節(jié)點都是不重要的,，則需要4個0表示其子節(jié)點信息,。同樣在SPIHT算法中，如果一棵樹的4個根節(jié)點不重要,，但是它的子節(jié)點是重要的,，則需要在LIP表中存儲4個根節(jié)點信息。這樣就造成了存儲空間的浪費,，也影響了編碼和解碼的速度,。
(4)在SPIHT算法中，需要維護三個動態(tài)鏈表,，使SPIHT算法的實現(xiàn)受到了硬件的限制,，不但增加了算法的復雜度，還造成了存儲空間的浪費,，阻礙了SPIHT算法的發(fā)展和推廣,。
3 改進算法
針對上述不足，提出了以下改進方案,。
3.1 改進方案1
實驗表明,，EZW算法和SPIHT算法的復雜度隨著某個位平面的重要系數(shù)個數(shù)的增加而增加。經(jīng)過三層整數(shù)小波變換后的圖像LL部分聚集了絕大部分能量,，重要系數(shù)的個數(shù)也比其他子帶要多許多,。而且人眼對LL部分的信息較為敏感,。考慮到LL3部分的重要性,，本文將LL3部分單獨編碼并采用無損圖像壓縮編碼的方法,。
經(jīng)過整數(shù)小波變換后的圖像其數(shù)據(jù)的浮動范圍較大，在某種程度上影響了壓縮的效果,。因此本文增加了一個DPCM的預測過程,，然后再對LL3部分進行Huffman編碼。
DPCM預測算法,以方便保留第一行和第一列的灰度值
for i=m/8:(-1):2
for j=n/8:(-1):2
LL3(i,j)=LL3(i,j)-
floor((LL3(i-1,j)+LL3(i,j-1))/2)
for i=m/8:(-1):2
LL3(i,1)=LL3(i,1)-LL3(i-1,1);
for j=n/8:(-1):2
LL3(1,j)=LL3(1,j)-LL3(1,j-1)
3.2 改進方案2
考慮LH,、HL,、HH子帶內(nèi)系數(shù)的相關性，對三個子帶取不同的熵值,，然后再進行EZW或SPIHT編碼,。這樣不但提升了解碼的精度，還簡化了運算,。對于某個子節(jié)點(i,j),，其子節(jié)點為（2i,2j）(2i+1,2j)(2i,2j+1)(2i+1,2j+1),不需要再在子帶內(nèi)部求子節(jié)點。
3.3 改進方案3
SPIHT算法在運行過程中需要維護3個動態(tài)鏈表,，要實現(xiàn)該算法對硬件的要求較高,，不利于該算法的實現(xiàn)和推廣,，因此本文選擇了矩陣+鏈表的改進算法,。將LIP和LSP都定義為一個矩陣，LIP是一個與圖像大小一致的矩陣,，用1 bit存儲不重要系數(shù)標志位,。LSP大小選擇要根據(jù)所研究的圖像來確定,對于每一個像素點需要用2 bit來存儲其位置信息。動態(tài)鏈表LIS繼續(xù)沿用原算法的定義,。算法實現(xiàn)過程為：
(1)初始化：
LIP={A1,，A2，A3}(A1,、A2,、A3的大小與L3、L2,、L1的大小相同)
LSP={B1,，B2，B3}（這里取B1,、B2,、B3的大小為L3、L2,、L1的1/4）
LIS=[(i,j,n)D/L](n表示層數(shù))
(2)初始化掃描：圖4為初始化LIP和LSP,；圖5為當LIS中n=1,type 為D的掃描方式,；圖6為當LIS中的n=1,type為L的掃描方式；圖7為當LIS中的n=2,，type為D的掃描方式,。
(3)第二次掃描只有LIP的掃描方式有所不同，如圖8所示,。對LIS的掃描與上述一致,。
改進的EZW算法和SPIHT算法完整流程圖如圖9所示。
4 實驗結(jié)果
本文通過在Matlab2010a上編程實現(xiàn)了上述4種算法,。
首先,，從主觀因素上對圖像質(zhì)量進行了分析，主要是在原算法和改進算法的掃描時間上進行了比較,。
其次,從客觀上對壓縮后圖像質(zhì)量進行了評估,，主要是通過PSNR(峰值信噪比)、MSE(均方誤差）,、RMS(均方根值誤差)這三方面進行比較分析,。
RMS=((x1-x)2+(x2-x)2+…+(xn-x)2)/n (3)
以下三組實驗選擇的圖像大小為64×64×8 bit的國際標準測試圖片lena、barb和boat,，三幅圖像的比特率均為0.25 bpp,。
表1為原EZW算法和改進算法在編碼時間和解碼時間的比較，圖10為用原EZW算法和改進算法解碼后的恢復圖像,，表2為用原EZW算法和改進算法對圖像進行壓縮后PSNR,、MSE、RMS的對比,。
以下三組實驗選擇的圖片大小為512×512×8 bit的國際標準測試圖片lena,、barb、boat,。
表3為原SPIHT算法和改進算法對實驗圖像進行不同比特率的編碼后,在PSNR,、MSE、RMS三方面的對比分析,。
圖11為原SPIHT算法和改進算法對實驗圖像進行解碼后的恢復效果圖,。這組實驗選擇的比特率為0.125 bpp。 圖12為用原SPIHT算法和改進算法對實驗圖像進行解碼后的恢復效果圖,。這組實驗選擇的比特率為0.25 bpp,。
基于整數(shù)小波變換的EZW算法和SPIHT算法不僅具有傳統(tǒng)圖像壓縮算法的所有優(yōu)點，而且還具有一些新的優(yōu)點,，如支持感興趣圖像編碼,，支持無損圖像壓縮等。本文以原EZW算法和SPIHT算法為基礎,，對圖像進行三層(5,3)整數(shù)小波變換以后對低頻部分進行DPCM+Huffman編碼,將高頻部分分為3個子帶分別進行編碼,。同時摒棄了原SPIHT算法的三鏈表結(jié)構(gòu),，采用了鏈表+矩陣的編碼方式。圖像在恢復效果和運行速度上都優(yōu)于原算法,。但是還有一些需要改進的地方,，如EZW算法中如果一個根節(jié)點重要但是其所有的子節(jié)點不重要，如何有效地存儲這個根節(jié)點,，如何使壓縮后圖像有更好的壓縮比和信噪比,，有待進一步研究。
參考文獻
[1] 趙榮椿,趙忠明.數(shù)字圖像處理導論[M]. 西安:西北工業(yè)大學出版社,1999.
[2] 羅家輝,馮平,哈力旦.MATLAB7.0在數(shù)字圖像處理中的應用[M].北京:機械工業(yè)出版社,2007.
[3] 岡薩雷斯.數(shù)字圖像處理(第2版)[M].阮秋琦,譯. 北京:電子工業(yè)出版社,2007.
[4] 張德豐. Matlab小波分析[M].北京:機械工業(yè)出版社, 2009.
[5] 和青芳.計算機圖形學原理及算法教程[M].北京:清華大學出版社,2006.
[6] JPEG2000 PartI: Final draft international standard (ISO/IEC FDISI 5444-1)[S].ISO/IEC JTC1/SC29/WG1N18855,Aug.2000.
[7] ABU-HAJAR A, SANKAR R. Enhanced patial-SPIHT for lossless and lossy Image[C].ICASSP,2003.
[8] RANI B, BANSAL R K, BANSAL D S.Comparative Analysis of wavelet filter using objective quality measures[R]. International Advance Computing Conference,2009.
[9] SAID A, PEARLMAN W A. A new,fast,and efficient image codec based on set partitioning in hierarchical tree[J]. IEEE Trans.Circuits Syst.Video Techno[R]l,1996.
[10] 楊杰.數(shù)字圖像處理及MATLAB實現(xiàn)[M].北京:電子工業(yè)出版社,2010.
[11] Jia Zhigang, Guo Xiaodong, Li Linsheng. A fast image compression algorithm based on SPIHT[C].IEEE,2009.