摘  要： 滅點(diǎn)是分層重建過程的重要信息,，其求解的準(zhǔn)確程度直接關(guān)系到最后三維重建的效果,。提出了一種基于Hough算法的直線聚類檢測方法求取圖像中的直線信息以及基于RANSAC的由直線信息估計(jì)滅點(diǎn)信息的改進(jìn)算法，以提高估計(jì)滅點(diǎn)的魯棒性,。經(jīng)試驗(yàn)證明,，將所提出的算法應(yīng)用到分層重建的系統(tǒng)中，在僅有兩幅圖像的情況下能準(zhǔn)確地對目標(biāo)模型進(jìn)行重建,。
關(guān)鍵詞： Hough,；直線聚類檢測；滅點(diǎn),；分層重建,；RANSAC

　三維重建是計(jì)算機(jī)視覺研究的核心問題之一。早期的三維重建主要利用黑白棋盤等結(jié)構(gòu)已知的標(biāo)定物事先進(jìn)行標(biāo)定,，求得攝像機(jī)內(nèi)參數(shù),，但這種方法只能應(yīng)付靜止和已知環(huán)境條件下的重建工作。1992年,，F(xiàn)augeras[1]提出自定標(biāo)和分層重建等概念成為三維重建中最活躍的一個(gè)研究領(lǐng)域,，之后許多學(xué)者在這一領(lǐng)域進(jìn)行了進(jìn)一步的研究[2-4]。分層重建將重建分成以下三個(gè)層次：射影重建,、仿射重建和度量重建,，重建過程相對早期傳統(tǒng)標(biāo)定更具有實(shí)用性好、靈活性強(qiáng)的特點(diǎn),。
　本文在僅有兩幅圖且沒有攝像機(jī)運(yùn)動的情況下,，提出了基于Hough直線聚類檢測方法,。該方法將直線有目的性地按角度進(jìn)行分組，以減少參與滅點(diǎn)估計(jì)的直線樣本,，降低估計(jì)算法復(fù)雜度,；然后提出一種改進(jìn)的RANSAC算法[5]。該算法結(jié)合極線幾何約束的評價(jià)函數(shù),，重新構(gòu)造了代價(jià)函數(shù),，進(jìn)而提高了原RANSAC算法估計(jì)滅點(diǎn)的魯棒性；最后闡述了根據(jù)不同的滅點(diǎn)對數(shù)情況構(gòu)建變換矩陣進(jìn)行分層重建的方法,。
由于沒有場景信息時(shí),，重建結(jié)果與真實(shí)模型相差一個(gè)全局縮放因子，而這并不影響視覺效果,，因此,，本文提到的歐氏重建均是指相差一個(gè)常數(shù)因子的重建。
1 重建方法
1.1 滅點(diǎn)
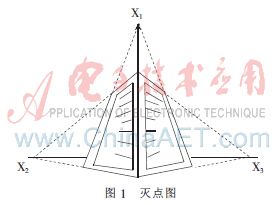
　空間上的一組平行線經(jīng)過透視投影成像后,，在成像平面上交于一點(diǎn),，稱為滅點(diǎn)，滅點(diǎn)圖如圖1所示,。圖中,，xp(p=1，2,，3)即為滅點(diǎn),。滅點(diǎn)信息一般用于攝像機(jī)參數(shù)的求解，是非標(biāo)定重建(如分層重建)的重要圖像信息,。滅點(diǎn)可以由直線檢測算法求取獲得,。

1.2 基于Hough的直線聚類檢測方法
　傳統(tǒng)算法中，主要由Burns提出了相位編組法(一種基于點(diǎn)梯度聚類的直線檢測方式[6]),，其算法易實(shí)現(xiàn)但目的性不強(qiáng)。本文采用受噪聲和曲線間斷的影響均較小的Hough[7]變換檢測直線方法,，獲取直線垂線和x軸正向的夾角(參數(shù)空間下的θ),，然后將參數(shù)空間的角度范圍由[-90°，90°]轉(zhuǎn)化為[0°,，180°],，得到直線按照角度分類的統(tǒng)計(jì)直方圖，橫坐標(biāo)為角度,，縱坐標(biāo)為在某角度范圍內(nèi)直線的個(gè)數(shù),。統(tǒng)計(jì)前一般需要對直線之間的間斷進(jìn)行預(yù)處理，通過設(shè)置間隔值減少參加估計(jì)滅點(diǎn)直線樣本的數(shù)量,。具體步驟如下：
　(1)將參數(shù)空間對應(yīng)的像素位置旋轉(zhuǎn)90-θ°,，以便使其大概位于一條垂線上,。
　(2)按旋轉(zhuǎn)的程度(如x值)來對這些像素位置排序。
　(3)利用一階微分函數(shù)找到裂口,，忽視掉小裂口,，合并間隔小的相鄰線段。
　(4)返回比設(shè)置的閾值長的線段信息,，并記錄θ,。
　(5)設(shè)立直方圖進(jìn)行聚類。
　Hough變換的缺點(diǎn)是既耗時(shí)又占空間,，因此,，本文采用概率Hough變換(PHT)改進(jìn)方法，減少了時(shí)間消耗和儲存空間的占用,。
　獲得統(tǒng)計(jì)直方圖后需要對不同方向上的直線進(jìn)行總體方向上的聚類(本文假設(shè)為三個(gè)方向,。兩個(gè)方向的情況與此相似，本文不予介紹),。聚類采用了下面的迭代方法：
　(1)對統(tǒng)計(jì)直方圖進(jìn)行曲線擬合(如高次樣條函數(shù)),。正常情況下一般可以獲得非邊緣2個(gè)局部最小值(波谷)作為圖像的分割閾值，即初始值T1,、T2(T1<T2),。
　(2)設(shè)將直線按角度分為n組，采用T1,、T2分割后得到直線集按角度由小到大依次為G1,、G2、G3,，求得G1,、G2、G3范圍內(nèi)每條直線平均角度為μ1,、μ2,、μ3，然后重新求分割閾值：
　T1=(μ1+μ2)/2,，T2=(μ2+μ3)/2
　(3)重復(fù)步驟(2),，直到T1、T2不再變化,。一般迭代2~3次就可收斂,。
1.3 改進(jìn)的魯棒估計(jì)滅點(diǎn)算法
　Schaffalitzky[8]、Rother[9-10],、陳付幸等人在利用直接信息檢測估計(jì)滅點(diǎn)時(shí)都引入了隨機(jī)抽樣一致性RANSAC算法,，一定程度上提高了單視圖求滅點(diǎn)的效率與準(zhǔn)確度。
本文基于二視圖極線幾何的關(guān)系，根據(jù)幾何約束調(diào)整代價(jià)函數(shù),，改進(jìn)了RANSAC估計(jì)滅點(diǎn)算法,，同時(shí)保證了算法的魯棒性與準(zhǔn)確性。
　假設(shè)m1,、m2互為匹配的滅點(diǎn)且為某無窮遠(yuǎn)點(diǎn)M到二視圖圖像的投影點(diǎn)的齊次坐標(biāo),，則m1~H∞m2(“~”表示相差一個(gè)常數(shù)因子)，且有mT2Fm1≈0,，即滅點(diǎn)在二視圖中仍然受到極線幾何約束,，且僅符合極線幾何關(guān)系的點(diǎn)才能考慮匹配。其中F(3×3)稱為基本矩陣,，其描述了雙攝像機(jī)的射影幾何關(guān)系,。

　其中，C1為滅點(diǎn)位于直線上的最小化,，C2為滅點(diǎn)位于極線上的最小化,，C3為滅點(diǎn)到直線的距離和最小化，C4為滅點(diǎn)到對應(yīng)極線距離和最小化,。相比較而言,，C1、C3之間和C2,、C4之間都有相近最小化的代數(shù)意義,，但是C3、C4比數(shù)值上的最小化C1,、C2代價(jià)函數(shù)更具有幾何意義,，更能反映極線幾何約束關(guān)系，所以本文選擇C3,、C4為評價(jià)滅點(diǎn)的雙重代價(jià)函數(shù),。
　本文改進(jìn)后的滅點(diǎn)估計(jì)算法步驟如下：
　(1)從檢測到的直線中按照方向進(jìn)行聚類，將分類中方向大致相同的直線隨機(jī)選擇M組數(shù)據(jù)樣本,，每組樣本的大小為3[8],，在一定的置信概率下，保證M組樣本中至少有一組樣本不包含錯(cuò)誤直線,。
　(2)分別估計(jì)M組樣本的滅點(diǎn),，并用所有直線段來檢驗(yàn)消失點(diǎn)(全數(shù)據(jù)檢驗(yàn))，通過C=C3C4代價(jià)函數(shù)選擇包含最多直線的滅點(diǎn)作為最優(yōu)滅點(diǎn),，將最優(yōu)滅點(diǎn)包含的直線作為局內(nèi)直線(inliers),。本步驟需要反復(fù)進(jìn)行,。
　(3)用劃分的inliers直線數(shù)據(jù)重新計(jì)算滅點(diǎn),，搜索附近外直線參加計(jì)算滅點(diǎn)。此步也可以重復(fù)進(jìn)行。
　(4)由步驟(3)獲得的穩(wěn)定的數(shù)據(jù)作為正確的inliers 直線數(shù)據(jù)來估計(jì)最終消失點(diǎn),。
1.4 射影重建,、仿射重建及歐氏重建
　本文根據(jù)獲取滅點(diǎn)信息的不同情況，分別進(jìn)行分層重建,。分層重建即按照射影幾何的層次關(guān)系依次實(shí)現(xiàn)射影重建,、仿射重建和歐氏重建。當(dāng)求得基礎(chǔ)矩陣后就可以獲得射影空間中的三維模型Xp,，其與真實(shí)場景模型Xe之間相差一個(gè)射影變換T,，則有：
　Xp=TAETAP Xe
　即確定無窮遠(yuǎn)平面π∞的位置(3個(gè)自由度)，獲得變換矩陣TAP,，將射影重建升級為仿射重建,，然后確定無窮遠(yuǎn)平面上絕對二次曲線ω的位置(5個(gè)自由度)，獲得變換矩陣TAE,，從而將仿射重建升級為歐氏重建,。
當(dāng)有3對滅點(diǎn)時(shí)，可線性求解π∞,，根據(jù)其滅點(diǎn)正交性線性求解ω,；當(dāng)少于3對滅點(diǎn)時(shí)，則采用模約束[2]等方式求解π∞及其對應(yīng)的單應(yīng)矩陣H∞,，由w=HT∞ ωH∞,，根據(jù)至少一對正交的滅點(diǎn)求解ω。對于單滅點(diǎn)的情況一般在多視圖下重建,。
1.5 誤差檢驗(yàn)
　本文采用反投影方法進(jìn)行誤差驗(yàn)證,。當(dāng)歐氏重建結(jié)束后，通過非線性最小化將空間點(diǎn)反投影到平面,，將投影后的點(diǎn)信息與原點(diǎn)的歐式距離作為評價(jià)誤差,，則有：

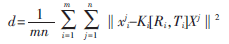
　其中，i為視圖數(shù),，j為每個(gè)視圖上的特征點(diǎn)數(shù),。根據(jù)誤差評價(jià)重建效果，若誤差較大可進(jìn)一步縮小1.2節(jié)和1.3節(jié)算法的閾值,，以增加準(zhǔn)確度,。
2 實(shí)驗(yàn)過程
　實(shí)驗(yàn)一：對一張如圖2所示的640×480的建筑物圖片，采用本文的直線聚類檢測算法進(jìn)行處理,，實(shí)驗(yàn)中分組數(shù)為180,。圖3為處理直線中小于5個(gè)像素的間斷連接的聚類情況(T1=46.380 9，T2=132.707 2),，圖4為圖3按單位度數(shù)進(jìn)行統(tǒng)計(jì)的直方圖,。對間斷點(diǎn)進(jìn)行處理，對間斷小于20像素的直線進(jìn)行合并，間斷點(diǎn)處理后直線提取如圖5所示,，其統(tǒng)計(jì)圖如圖6所示,。圖4、圖6的橫坐標(biāo)表示直線方向(單位為度),，縱坐標(biāo)表示按某個(gè)組間間隔分組的每組直線數(shù)量,。本文按角度分為180組，即組間間隔為1°,。

　由圖5,、圖6可以看到，通過直線段的連接,，調(diào)整間隔連接為15個(gè)像素,，可使直線的數(shù)量減少，達(dá)到合并和減少樣本的目的(T1=46.303 9,，T2=132.638 4),。
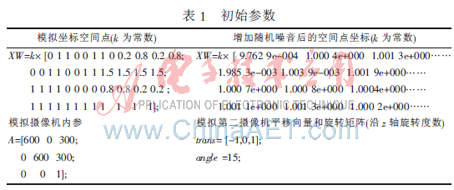
　實(shí)驗(yàn)二：采用實(shí)驗(yàn)室系統(tǒng)來模擬分層重建[11]，生成空間以XW為頂點(diǎn)物體(形如小房子)并沿z軸平移5個(gè)單位,，隨機(jī)增加0~0.002的噪音,。模擬如表1、表2的初始內(nèi)參A,，通過A將三維點(diǎn)信息投影到模擬的二視圖平面(模擬攝像機(jī)位置)上,，讓其中一個(gè)攝像機(jī)位于坐標(biāo)軸中心，其分層重建模型如圖7所示,。本文所有實(shí)驗(yàn)使用同一觀察視角(函數(shù)view(200,，20))。圖7~圖11(x,，y,，z)為坐標(biāo)系模擬物體所在的三維空間，單位為數(shù)值1,。

　進(jìn)行分層重建的步驟如下：
　(1)射影重建：根據(jù)模擬照相機(jī)中的二維點(diǎn)求取基礎(chǔ)矩陣后進(jìn)行射影重建,，其效果圖如圖8所示。
　(2)仿射重建：原物體XW點(diǎn)附近隨機(jī)添加帶噪聲點(diǎn)10個(gè),，以這些點(diǎn)連接的直線作為樣本,，然后通過本文算法估計(jì)3個(gè)正交方向3對滅點(diǎn)，根據(jù)無窮遠(yuǎn)性質(zhì)獲得變換矩陣進(jìn)而完成仿射重建,，其效果如圖9,、圖10所示。

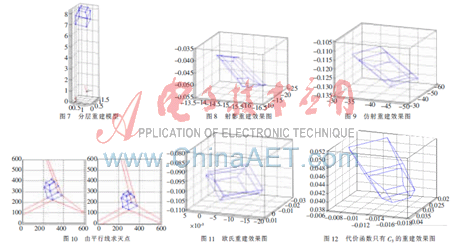
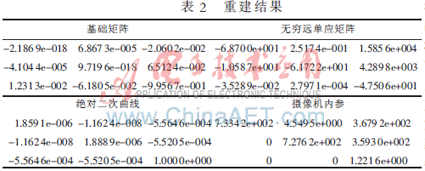
　(3)歐氏重建：由3對滅點(diǎn)線性求得絕對二次曲線的圖像進(jìn)行歐氏重建(相差一個(gè)常數(shù)因子),，其結(jié)果如圖11所示,，實(shí)驗(yàn)結(jié)果如表2所示,。
　通過與傳統(tǒng)代價(jià)函數(shù)只有C3算法作為評價(jià)比較，其重建效果如圖12所示,，由圖可以得出本文算法能夠獲得較準(zhǔn)確的估計(jì)滅點(diǎn)，從而獲得更好的分層重建效果,。估計(jì)滅點(diǎn)的比較如表3所示,。

　本文方法主要是基于二視圖的重建方法，當(dāng)滅點(diǎn)為兩對或更少時(shí)可采用多視圖增加約束的方法實(shí)現(xiàn),。
　本文主要介紹了分層重建中滅點(diǎn)信息的求取過程中兩個(gè)階段的研究,，即首先采用直線聚類檢測方法檢測直線，然后將分類后的直線樣本通過改進(jìn)的RANSAC估計(jì)算法類進(jìn)行滅點(diǎn)估計(jì),。將直線檢測與滅點(diǎn)的估計(jì)融合在一起,，提高了滅點(diǎn)求取算法的效率和魯棒性，使滅點(diǎn)的估計(jì)更具有針對性,，同時(shí)根據(jù)得到的滅點(diǎn)信息結(jié)果介紹了對應(yīng)的重建策略,。本方法進(jìn)行了分層重建，并通過模擬實(shí)驗(yàn)得到了理想結(jié)果,。
參考文獻(xiàn)
[1] FAUGERAS O D. Stratification of 3-D vision： projective,， affine and metric representations[J]. Journal Optical Society of America， 1995,，12(3)：465-484.
[2] POLLEFEYS M,， GOOL V L， OOSTERLINCK A. The modulus constraint： A new constraint for self-calibration[C]. Proceedings  of  International Conference on Pattern Recognition,， Vienna,， Austria， 1996： 349-353.
[3] TRIGGS B. Auto-calibration and the absolute quadric[C].Proceedings of IEEE Conference on Computer Vision and Pattern Recognition,， Puerto Rico,， USA， 1997：610-614.
[4] HARTLEY R I. Euclidean reconstruction and invariants from multiple images[J].IEEE Transactions on Pattern Analysis and Machine Intelligent,，1994,，16(10)： 1020-1041.
[5] FISCHLER M A， BOLLES R C . Random sample consensus： a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM,， 1981,，24(6)： 380-395.
[6] BURNS J B， HANSON A R. RISEMAN E M. Extracting straight lines[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,，1986(4).
[7] LINGWORTH J,， KITTLER J.A survey of the Hough transforms [J]. CVGIP， 1988,，44：87-116.
[8] SCHAFFALITZKY F,， ZISSERMAN A. Planar grouping for automatic detection of vanishing lines and points [J]. Image and Vision Computing,， 2000，18(9)： 645-658.
[9] ROTHER C. A new approach for vanishing point detection in architectural environments[C]. British Machine Vision Conference (BMVC),， Bristol,， UK， 2000： 382-392.
[10] ROTHER C . Multi-view reconstruction and camera recovery using a real or virtual reference plane[C]. PhD thesis,， Royal Institute of Technology,， Sweden， 2003.
[11] Yi Ma. An invitation to 3d vision[EB/OL]. http：//vision.ucla. edu/MASKS,，2010-12-10.