鎖相環(huán)是倍頻電路的主要實(shí)現(xiàn)方式,直接決定倍頻的成敗。傳統(tǒng)的鎖相環(huán)各個(gè)部件都是由模擬電路實(shí)現(xiàn)的,隨著數(shù)字技術(shù)的發(fā)展,全數(shù)字鎖相環(huán)逐步發(fā)展起來(lái),全數(shù)字鎖相環(huán)的環(huán)路部件全部數(shù)字化,通常由數(shù)字鑒相器、數(shù)字環(huán)路濾波器、壓控振蕩器以及分頻器組成,全數(shù)字鎖相環(huán)中的分頻器要求模可預(yù)置且可根據(jù)實(shí)際需要進(jìn)行可逆分頻[2]。由于現(xiàn)有的電路均不能滿足上述要求,本文首先采用simuink 和FPGA 開(kāi)發(fā)了應(yīng)用于倍頻電路的變模可逆分頻器。
2. 變模可逆分頻器的工作原理
變模分頻器的基本原理是設(shè)置一個(gè)符合函數(shù),在分頻過(guò)程中,觸發(fā)器的輸出與預(yù)置模比較,當(dāng)觸發(fā)器的輸出與預(yù)置模一致時(shí),則給出符合信號(hào),強(qiáng)迫計(jì)數(shù)器進(jìn)入所希望的狀態(tài),即初始狀態(tài),隨后計(jì)數(shù)器則按照卡諾圖確定的程序繼續(xù)工作,直到最后一個(gè)狀態(tài),即由地址碼確定的第N-1 個(gè)狀態(tài),再?gòu)?qiáng)迫分頻器回到初始狀態(tài)[3]。所以每個(gè)觸發(fā)器應(yīng)當(dāng)受到兩個(gè)控制函數(shù)的控制,即:
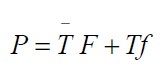
f—正常的由卡諾圖得到的控制函數(shù);
F—強(qiáng)迫分頻器進(jìn)入的希望狀態(tài);
T—符合函數(shù);
當(dāng)符合函數(shù)T = 1時(shí),F(xiàn) 不起作用,P = f ,分頻器按正常程序分頻;當(dāng)T = 0,F(xiàn) 起作用,P = F ,強(qiáng)迫分頻器跳變到所希望的狀態(tài)。
表1 狀態(tài)轉(zhuǎn)換表
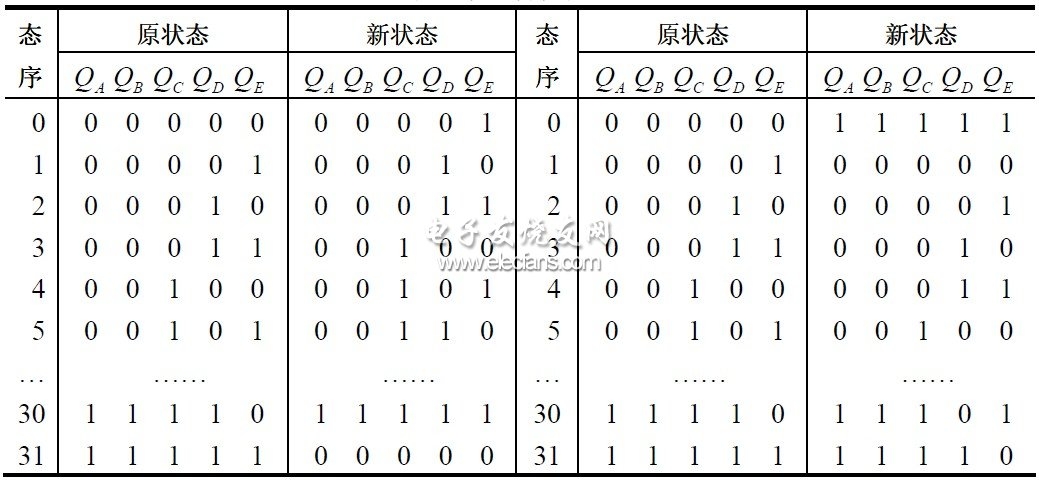
(注:表1 為狀態(tài)轉(zhuǎn)換圖,其中左半部分為遞增分頻器狀態(tài)轉(zhuǎn)換表,右半部分為遞減狀態(tài)轉(zhuǎn)換表。表2 為計(jì)數(shù)值與各觸發(fā)器當(dāng)前值的關(guān)系。)
表2 計(jì)數(shù)值與各觸發(fā)器當(dāng)前值的關(guān)系
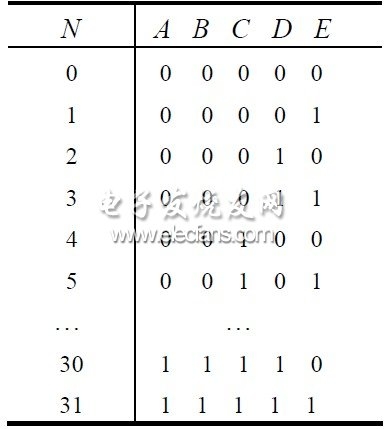
加法分頻器的驅(qū)動(dòng)方程為:

減法分頻器的驅(qū)動(dòng)方程為:

各觸發(fā)器還受到可逆信號(hào)的控制,當(dāng)I _ D信號(hào)為1時(shí)為遞增分頻器,反之為遞減分頻器。
各觸發(fā)器的驅(qū)動(dòng)函數(shù)為:
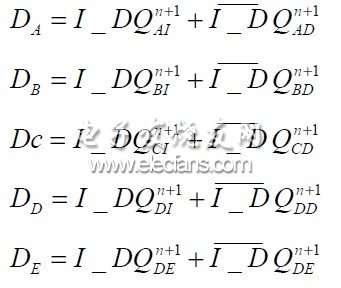
3. 基于simulink的可逆分頻器設(shè)計(jì)
采用simulink 建立可逆分頻器模型,如圖1 所示。分頻器采用五級(jí)D 觸發(fā)器實(shí)現(xiàn),輔之以必要的控制邏輯。輸入端A、B、C、D、E 為輸入模值,I _ D為1 時(shí)分頻器工作在遞增模式,當(dāng)I _ D為0時(shí)分頻器工作在遞減模式,符合函數(shù)的輸出T連接至D觸發(fā)器的清零端,分頻器的工作波形如圖2 所示。從圖中可以看出分頻器能夠在預(yù)置模下完成遞增或遞減分頻器功能。
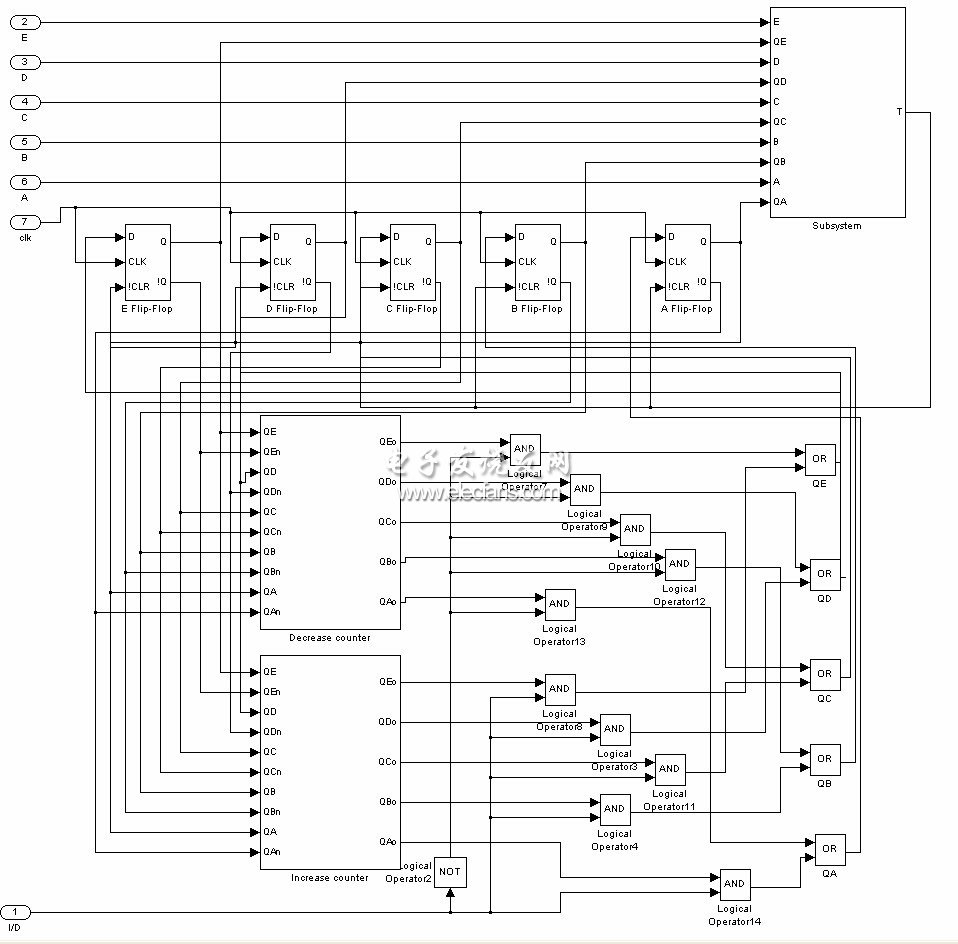
圖1 五級(jí)分頻器
圖2 分頻器的工作波形。
圖3 分頻器的仿真波形。
4. 基于FPGA的可逆分頻器設(shè)計(jì)
采用verilog 語(yǔ)言實(shí)現(xiàn)了可逆分頻器,其仿真波形如圖3 所示,分頻器可完成預(yù)置模以及遞增及遞減分頻功能。分頻器的verilog 代碼如圖4 所示,寄存器傳輸級(jí)網(wǎng)表如圖5 所示。
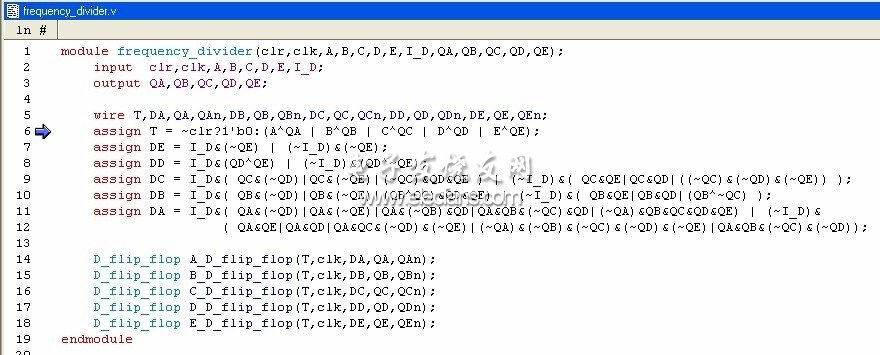
圖4 分頻器代碼。
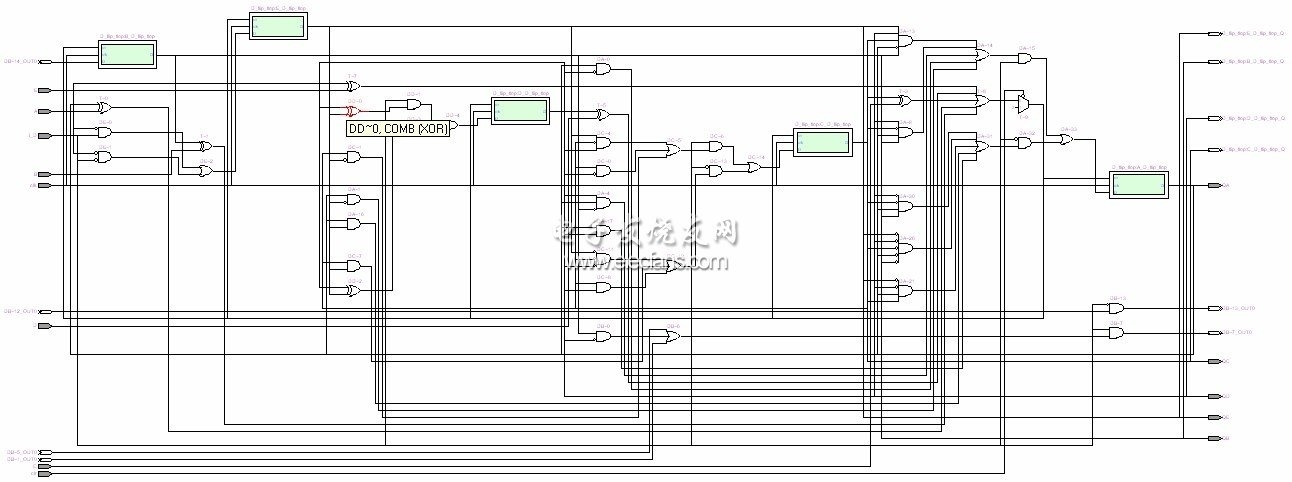
圖5 寄存器傳輸級(jí)網(wǎng)表。
5. 總結(jié)
本文分析了變模可逆分頻器的工作原理,并分別采用simulink 和FPGA 實(shí)現(xiàn)了可逆分頻器。仿真結(jié)果表明分頻器能夠完成預(yù)置模,遞增和遞減分頻功能,滿足設(shè)計(jì)要求。

