摘 要： 針對(duì)序列模式的幾個(gè)經(jīng)典的算法的缺點(diǎn)，提出了一種基于時(shí)間約束序列模式的快速產(chǎn)生候選項(xiàng)的方法（TFEGC）,。此算法不但避免了頻繁的掃描數(shù)據(jù)庫,，還考慮了時(shí)間限制因素，避免了無用的候選序列的產(chǎn)生,，提高了算法運(yùn)行的時(shí)間效率,。
關(guān)鍵詞： 序列模式挖掘；時(shí)間約束,；候選項(xiàng);快速產(chǎn)生
序列模式挖掘在很多領(lǐng)域都具有十分重要的意義,，比如它可以根據(jù)分析顧客購買行為來決定商品的擺放位置，從而制定商場的營銷策劃,。所以,，近年來出現(xiàn)了很多序列模式挖掘的改進(jìn)算法，目前提出算法中,，有兩類比較典型：GSP[1]算法和采用分治策略來進(jìn)行模式增長的PrefixSpan[2]算法,。但是這兩種算法都存在一定的缺點(diǎn),。參考文獻(xiàn)[3]中提出的快速有效的產(chǎn)生候選項(xiàng)的FEGC算法，不需要多次掃描數(shù)據(jù)庫,，且不需要在前一次迭代的基礎(chǔ)上來產(chǎn)生候選項(xiàng),，也不需對(duì)非頻繁項(xiàng)進(jìn)行剪枝或修剪，能夠達(dá)到快速產(chǎn)生候選項(xiàng)的效果,。但是,，F(xiàn)EGC算法是針對(duì)數(shù)據(jù)庫總體的序列來產(chǎn)生候選項(xiàng)的，有些并不是有效的和用戶感興趣的序列,，這在實(shí)際應(yīng)用中就耗費(fèi)了大量的時(shí)間和空間,，如分析顧客的購買行為，就不需要將其一月份購買的產(chǎn)品和十二月份購買的產(chǎn)品放在一起進(jìn)行研究比較,。所以本文在FEGC算法的基礎(chǔ)上將時(shí)間限制因素加了進(jìn)去,，可稱之為TFEGC算法，本算法繼承了FEGC算法的優(yōu)點(diǎn),，而且避免了不必要的,、無用的一些候選項(xiàng)的產(chǎn)生，提高了算法的運(yùn)行效率,，且在序列結(jié)合的過程中,，只需檢查uid、fid(t)以及s(t)的值,，便可知道與哪些項(xiàng)進(jìn)行結(jié)合,，無須再進(jìn)行檢驗(yàn)。
1 相關(guān)算法介紹
GSP算法,，即廣義序列模式算法,，使用序列模式的向下封閉性，并采用多次掃描的候選產(chǎn)生-測試方法,，它是由Srikant和Agrawal于1996年提出的,。它的主要思想是利用序列模式的種子集，即前次掃描得來的序列模式來產(chǎn)生潛在的頻繁序列,，即候選序列,，每個(gè)候選序列都會(huì)比產(chǎn)生它的種子序列模式多包含一個(gè)項(xiàng)。直到一遍掃描不能產(chǎn)生新的序列模式或者新的候選序列時(shí),，算法終止,。
PrefixSpan算法是前綴投影序列模式增長算法[4]，此算法的特點(diǎn)是不需要產(chǎn)生候選項(xiàng),，算法思想是先找出各個(gè)頻繁項(xiàng),，然后分別產(chǎn)生它們所對(duì)應(yīng)的投影數(shù)據(jù)庫,，接著對(duì)各個(gè)投影數(shù)據(jù)庫進(jìn)行挖掘,，最后將前綴模式與后綴模式相連得到頻繁序列。此算法的缺點(diǎn)就在于可能會(huì)產(chǎn)生大量的投影數(shù)據(jù)庫，而且要掃描數(shù)據(jù)庫多次[3],。
FEGC算法的特點(diǎn)有：（1）Head,、Body、Tail的引入,，在一個(gè)交易序列中,，處于Head的項(xiàng)在形成二序列時(shí)，只能作為二序列中的Head,，處于Body的項(xiàng)在形成二序列時(shí),，既可以作為Head,也可以作為Tail；（2）Nid的引入,，Nid的作用是用來規(guī)定在形成候選序列的過程中的2-序列的結(jié)合順序[1],。
2 TFEGC算法的理論和相關(guān)概念
對(duì)于給定的某個(gè)顧客的交易數(shù)據(jù)序列B={(Item，TID),，…},其中Item表示交易的項(xiàng),，TID表示交易的時(shí)間，設(shè)I={(i1,，t1),，(i2，t2),，…(in,，tn)}是由n個(gè)不同的項(xiàng)組成的序列，它記錄了某個(gè)顧客在不同的時(shí)間購買的產(chǎn)品,，然后根據(jù)時(shí)間限制將這個(gè)序列劃分成不同的子序列,，再將這些子序列轉(zhuǎn)化為2-序列[5]，最后以這些2-序列為基礎(chǔ),，找出所有的候選項(xiàng),。
2.2 公式的應(yīng)用及td的引入
上面的三個(gè)公式都是為了解決利用TFEGC算法來求候選項(xiàng)時(shí)遇到的問題，它們所發(fā)揮的作用可通過下面的具體例子來進(jìn)行詳細(xì)描述,。
由圖1可知所有的2-序列過程,，下面以子序列<bcde>產(chǎn)生的2-序列<bc>為例，具體過程如下：
（1）計(jì)算出uid=4-2=2,，fid(c)=4-2=2,，fid(d)=4-3=1，s(c)=2-1=1,，s(d)=3-1=2,；
（2）對(duì)于2-序列<bc>，因?yàn)閟(c)=1,，說明它只能與排在子序列<bcde>之后的第一個(gè)子序列產(chǎn)生的2-序列相結(jié)合,，由圖1可知是子序列<cdef>產(chǎn)生的2-序列,；又因?yàn)閒id(c)=2，說明它只能與<cdef>產(chǎn)生的前兩個(gè)2-序列<cd>,、<ce>相結(jié)合,，生成<bcd>、<bce>,；又因?yàn)閟(d)=2,、fid(d)=1，說明<bcd>還可以與排在子序列<bcde>之后的第二個(gè)子序列<def>產(chǎn)生的第一個(gè)2-序列<de>進(jìn)行結(jié)合,生成<bcde>,e為子序列<bcde>的最后一項(xiàng),，不作考慮,。
由上面的步驟（2）可知，雖然求得了s(c)的值,，但是在算法的實(shí)現(xiàn)過程中,，并不知道子序列<cdef>就是排在子序列<bcde>之后的第一個(gè)子序列，為了解決這個(gè)問題,，引入了td的值,，為節(jié)省存儲(chǔ)空間，可以用矩陣的形式來存儲(chǔ)td的值,，如圖2所示,。
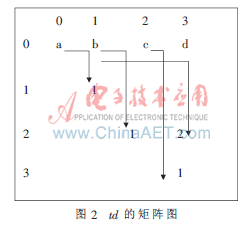
矩陣中沒有出現(xiàn)項(xiàng)e和項(xiàng)f，因?yàn)轫?xiàng)f為序列的最后一項(xiàng),，所以它不會(huì)與任何二序列進(jìn)行結(jié)合,，由圖1知并沒有產(chǎn)生以e為首項(xiàng)的子序列，所以不會(huì)產(chǎn)生以e為首項(xiàng)的2-序列,。
其中,，[1，1]=1-0=1,表示排在以a為首字母的子序列之后的第一個(gè)子序列,，是以b為首字母的子序列,；[2，2]=2-1=1,，表示排在以b為首字母的子序列之后的第一個(gè)序列,，是以c為首字母的子序列,依此類推。
所以,，當(dāng)算出s(t)的值時(shí),，只需比較其與td的值，當(dāng)s(t)=td的值時(shí),，則此序列就是所要結(jié)合的2-序列,。
3 TFEGC算法
3.1 算法思想
本算法一共有四大步，第一步是根據(jù)時(shí)間限制將原序列劃分為多個(gè)子序列,；第二步是將得到的子序列轉(zhuǎn)化為2-序列,；第三步是根據(jù)uid,、fid(t)和s(t)的值將2-序列進(jìn)行結(jié)合，從而得到所有的候選項(xiàng),；第四步根據(jù)最小支持度minsup得到頻繁項(xiàng)集,。
從上所述可以看出,，此算法的主要特點(diǎn)有：(1)加入了時(shí)間限制因素,；(2)只需要掃描數(shù)據(jù)庫一次，節(jié)省了算法的運(yùn)行時(shí)間,；(3)引入了uid,、fid(t)、s(t),，使之在形成n-序列的過程中,，能夠準(zhǔn)確地找到要結(jié)合的2-序列，不需要掃描所有子序列產(chǎn)生的二序列,，提高了算法的時(shí)間效率,。
3.2 TFEGC核心算法描述
2-序列結(jié)合的算法如下：
for all I∈DB{ //I為滿足時(shí)間限制的子序列
l=strlen(I)；
uid=l-2,；
for(n is smaller thanl ){
if(in∈I and n≠1 and n≠1)
{ //in不能為首尾兩項(xiàng)
s(in)=n-1,；
fid(in)=l-n；}
}
for(scan the Matrix Chart of td){//掃描矩陣td
if(td==s(in)){
record the item r and
record those 2-sequence se whose first item is r,；}
//r用來存放首項(xiàng),，se用來
//存放以其為首項(xiàng)形成的2-序列
}
for all tn∈se{
if(tn.index==fid(in)){//找到所要結(jié)合的2-序列
in+tn；}//2-序列in和2-序列tn相結(jié)合
}
}
3.3 算法舉例
為了進(jìn)一步描述TFEGC算法,，以圖1中的子序列<abc>產(chǎn)生的第一個(gè)2-序列<ab>為例,，求以這個(gè)2-序列為基礎(chǔ)所形成的候選項(xiàng)過程，如圖3所示,。
4 實(shí)驗(yàn)結(jié)果
算法實(shí)驗(yàn)環(huán)境為PentiumⅣ3.0 GHz雙核 PC機(jī)器,，內(nèi)存為1 GB，Windows XP操作系統(tǒng),，采用C++語言在VC編程環(huán)境下實(shí)現(xiàn),。實(shí)驗(yàn)測試數(shù)據(jù)采用IBM數(shù)據(jù)生成器，該生成器是目前數(shù)據(jù)挖掘相關(guān)研究中使用廣泛和權(quán)威的生成器,，可以通過設(shè)置參數(shù)生成不同特性的數(shù)據(jù)集,，具體參數(shù)含義如表1所示。
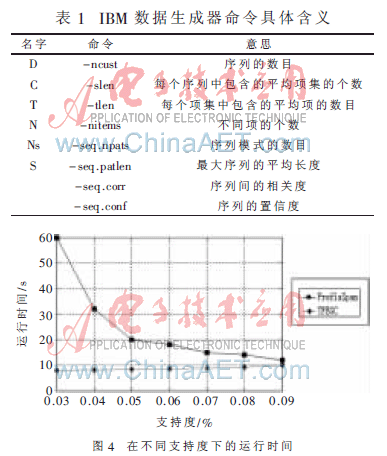
PrefixSpan算法和TFEGC算法在不同的支持度下的運(yùn)行時(shí)間如圖4所示,，從結(jié)果可以看出文中提出的方法優(yōu)于PrefixSpan算法,，因?yàn)門FEGC算法只需要掃描數(shù)據(jù)庫一次，而且由于uid,、fid(t)以及s(t)的引入,，避免了一些無用序列的產(chǎn)生,，大大減少了運(yùn)行時(shí)間。
圖5所示的是FEGC和TFEGC在不同數(shù)量的顧客下算法的運(yùn)行時(shí)間,，從中也可以看出TFEGC算法的運(yùn)行時(shí)間少于FEGC算法的運(yùn)行時(shí)間,。這是因?yàn)樵诙蛄械慕Y(jié)合過程中，TFEGC不需要逐個(gè)掃描其他的二序列,，只需查看uid,、fid(t)以及s(t)的值就可以判斷應(yīng)該與哪些二序列進(jìn)行結(jié)合，而且生成的用戶不感興趣的序列也大大減少了,。因?yàn)榧尤肓藭r(shí)間的限制,，所以根據(jù)支持度來提取頻繁序列的時(shí)間也就相應(yīng)地減少了。
本文提出的算法,，可由用戶自己設(shè)定時(shí)間限制來查找頻繁序列,，也可以用來處理不同數(shù)量的客戶群，所以具有一定的靈活性,。又因?yàn)槠渲粧呙钄?shù)據(jù)庫一次,，而且二序列的結(jié)合也具有一定的明確性，所以在時(shí)間效率上具有一定的優(yōu)越性[6],。
參考文獻(xiàn)
[1] SRIKANT R,，AGRAWAL R.Mining sequential patterns:generalizations and performance improvements[C].Proc.of Int’l Conf.on Extending Database Technology，1996：3-17.
[2] PEI J,，HAN J,，Mortazavi-Asl B，et al.Prefixspan: mining sequential patterns efficiently by prefix-projected pattern growth[C].Proc.of Int.Conf.on Data Eng. (ICDE’01),，2001：215-224.
[3] Liao Weicheng,，Yang Donlin，Wu Jungpin,，et al.Fast and effective generation of candidate-sequences for sequential pattern mining[C].2009 Fifth International Joint Conference on INC,，IMS and IDC，2009:2006-2009.
[4] 趙暢,，楊冬青,，唐世渭.Web日志序列模式挖掘[J].計(jì)算機(jī)應(yīng)用，2000,，9（20）：13-16.
[5] 連一峰,，戴英俠，王航.基于模式挖掘的用戶行為異常檢測[J].計(jì)算機(jī)學(xué)報(bào),，2002,，25(3)：325-329.
[6] 吉根林，帥克，孫志揮．?dāng)?shù)據(jù)挖掘技術(shù)及其應(yīng)用[J].南京師范大學(xué)學(xué)報(bào)(自然科學(xué)版),，2000,，23(2)：25-27.