摘　要: 以分層遞階智能控制為基礎框架,，提出了基于控制任務的某些時域性能指標的智能控制任務適應算法,，對運行控制級動態(tài)建立特征模型，迫使系統(tǒng)逼近理想控制軌跡,，從而提高控制性能,。
　　關鍵詞: 智能控制 任務自適應 特征模型 上(下)界特征直線 特征點

　　實際系統(tǒng)由于存在非線性,、不確定性、時變性和不完全性等因素,，一般無法獲得系統(tǒng)精確的數(shù)學模型,，而且為了提高控制性能，整個系統(tǒng)變得較為復雜,，增加了設備的初投資,，降低了系統(tǒng)的可靠性。在這種背景下,，無需人的干預就能自主地驅動智能機器實現(xiàn)其目標的智能控制誕生了,。直到目前，傳統(tǒng)控制理論中的各種動態(tài)性能指標只能作為智能控制的事后評價標準,，無法作為智能控制系統(tǒng)的設計依據(jù),。
　　Saridis曾提出智能控制系統(tǒng)的分層遞階結構，奠定了智能控制的三元結構的理論基礎^[1],。在此基礎上,，周其鑒、李祖樞等人提出仿人智能控制(HSIC),，并建立了仿人智能控制的基本理論,，給出了仿人智能控制器的設計方法^[2][3]。李祖樞,、涂亞慶等提出的設計方法以相平面(e－e′)作為信息空間設計控制器,。由于相平面(e－e′)只是隱含了時間信息，難以與性能指標建立直接聯(lián)系,，因此這是一種定性的設計方法,。然而控制系統(tǒng)設計的目標，總是針對控制系統(tǒng)完成的任務,，滿足于特定的性能指標^[4],。基于這種思想,，本文提出了面對不同任務的某些時域指標,，按照分層遞階控制的框架，以(e－t)為信息空間設計智能控制器的方法,，并給出了任務適應算法,。由于(e－t)信息空間明顯包含了e′的信息，并且可以直接與時域性能指標相聯(lián)系,，因此,，該設計方法是一種定性與定量相結合的設計方法,。
1 智能控制任務適應的基本思想
　　按照分級遞階智能控制的基本理論，整個系統(tǒng)由中樞司令級,、組織協(xié)調級和單元控制級構成,。單元控制級又可分解為任務適應級(TA)、參數(shù)校正級(ST)和運行控制級(MC),。運行控制級直接面向被控對象,，采用產生式系統(tǒng)結構。知識庫用三重序元＜Φ,，Ψ,，Ω＞描述。其中,，Φ＝{Φ₁,，Φ₂，…,，Φ_n}稱為特征模型,，Ψ＝{Ψ₁,Ψ₂,…，Ψ_r}稱為控制(決策)模態(tài)集,，Ω＝{ω₁,，ω₂，…,，ω_q}為產生式集,。產生式ω_i(i＝1，2,，…,，q)可表示為
　　IF Φ_i THEN Ψ_i, Φ_i∈Φ， Ψ_i∈Ψ
　　其中Φ_i稱為特征狀態(tài),，是特征信息空間劃分的一個區(qū)域,；Ψ_i是控制器的輸出量U與輸入信息R、特征記憶Λ之間定量或定性關系的描述,。
　　MC級的控制目標主要是控制精度，即滿足特定任務的某些時域性能指標,。為了適應不同的任務,，滿足相應的性能指標，MC級的知識庫＜Φ,，Ψ,，Ω＞應該適應不同的任務。
　　無論是定值控制還是伺服控制,，控制過程總是期望系統(tǒng)的動態(tài)響應在時相空間(e－e′－t)為一條理想軌跡,。換言之,，這條理想軌跡作為設計智能控制器的目標，軌跡上的每一點都被視為控制過程中的瞬態(tài)指標,。這條理想軌跡可以分別向(e－t),、(e′－t)和(e－e′)三個平面投影，根據(jù)分析的側重點考慮這三條投影曲線中的一條或幾條,，從而簡化設計目標,。由于被控對象具有不確定性且又不確知，實際上運動的軌跡只可能處在這條理想曲線周圍的一個曲柱中,。智能控制器的設計任務就是以實際軌跡與理想軌跡在信息空間中的偏差軌跡為依據(jù),，對信息空間(e－e′－t)進行劃分(特征模型)，并給出相應的控制模態(tài),。
　　在HSIC的基本算法中,，特征模型的建立即特征狀態(tài)的劃分是一種近乎先驗的過程^[2][3]。換言之,，特征變量的閾值確定是純粹的經驗判斷,，它不依對象的不同而自動設置，也不會根據(jù)實際過程的輸出響應和偏差曲線做動態(tài)調整,，更無法依據(jù)控制指標的要求變化而適應,。這在相當大的程度上限制了控制任務的正確完成。本文提出的動態(tài)建立特征模型的算法是一種任務自適應的方法,。根據(jù)系統(tǒng)的瞬態(tài)性能指標的要求,，在線辨識出過程的純時延，結合上升時間t_r,、超調量δ_p和峰值時間t_p劃分(e－t)平面,，實時給出MC級特征狀態(tài)的切換閾值，動態(tài)地建立其特征模型Φ,，改變其知識庫,，迫使控制沿著適當?shù)能壽E達到各項控制指標?；谶@種思想,，通過對控制的偏差曲線進行幾何分析，給出任務適應級TA對MC級特征基元的實時調整方法,。
2 任務適應算法及仿真實驗
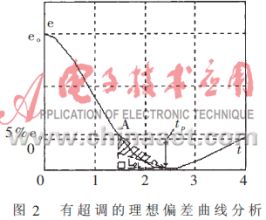
　　對于限制上升時間t_r,、超調量δ_p和峰值時間t_p的伺服跟蹤控制系統(tǒng)，我們考慮穩(wěn)態(tài)誤差e_ss＝e(∞)×5%的性能要求,，如圖1所示,。引入上升時間特征點A、第一上界特征直線L_1u,、第一下界特征直線L_1l三個概念,，并由此導出HSIC的任務適應算法,，確定對信息空間劃分的特征模型?？紤]上升時間t_r,、超調量δ_p和峰值時間t_p的要求，進一步引入峰值特征點B,、第二上界特征直線L_2u和第二下界特征直線L_2l的概念,，如圖2所示。

　　我們以直線L_1u作為特征變量的閾值軌跡之一,。只要實際偏差e(t)在時段(0,t_r)內的值都在直線L_1u的下方,，就可以確保滿足性能指標上升時間t_r。我們把直線L_1l定義成特征變量的閾值軌跡,，其目的是滿足t_r的同時,，使系統(tǒng)的輸出響應盡量避免超調。于是規(guī)定理想偏差曲線e₁(t)介于L_1u和L_1l兩條直線之間,，即圖1中的陰影區(qū)域內,。
　　類似地，對于時間段(t_r,t_p),，理想偏差曲線e₂(t)應介于特征直線L_2u和L_2l之間,，如圖2中的陰影區(qū)域所示。在上述定義的特征點,、特征直線的基礎上,，對信息空間進行劃分，建立相應特征模型如下：
　　Φ₁＝{Φ₁,，Φ₂,，Φ₃，Φ₄,，Φ₅,，Φ₆，Φ₇}
　　
　　這里對于Φ₂,、Φ₅和Φ₇可以采用保持控制模態(tài),。
　　類似地，還可以對時間段(t_p,∞)的偏差曲線做進一步分析,。需要指出,，這里定義的第一、二下界特征直線是經驗直線,，根據(jù)現(xiàn)場專家對于控制環(huán)境和對象的了解來確定。出于簡化考慮,，本文將這條閾值軌跡設定為角平分線,。
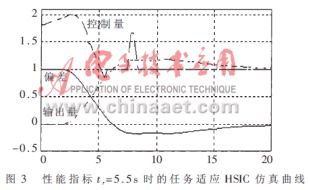
　　設受控對象傳遞函數(shù)為,，輸入為單位階躍函數(shù)，性能要求是上升時間t_r＝5.5s,，超調量δ_p＝20%,峰值時間t_p＝9s,。
　　仿真結果如圖3所示，表明本文提出的任務適應算法能夠較好地滿足控制性能指標的要求,，具有很強的任務適應性,。如果通過ST級對MC級控制模態(tài)中的控制參數(shù)進行在線校正，控制效果會更好,。