摘  要： 在變形雅可比(p=4,q=3)-傅里葉矩的基礎上采用三次樣條擬合特征空間軌跡,，保證了插值函數(shù)光滑性,，并且通過限定每個三次多項式的一階和二階導數(shù)，使其在斷點處相等,，成功地逼近每對斷點間的曲線,，從而能夠更好地對曲線進行擬合，并驗證包含圖像信息量最大的矩值,。
關鍵詞： 不變矩,；多焦面圖像,；三次樣條；擬合

    變形雅可比(p=4,q=3)-傅里葉矩[1-6]是對于圖像的平移,、旋轉(zhuǎn),、灰度、尺度等多種畸變不變性和噪聲不敏感,，具有基本不變值的矩,，并且用于圖像的特征提取時，只用一個很小的圖像描述量集合就可以代表圖像,。變形雅可比矩反映了圖像函數(shù)到一些特定基本函數(shù)的映射關系,，從而確保了由一定數(shù)量的不變矩作為描述量描述圖像的可能性和可靠性。由于變形雅可比矩是一種高度濃縮的圖像特征,，具有平移,、尺度、旋轉(zhuǎn)等多畸變不變性,，因此變形雅可比矩和矩函數(shù)被廣泛用于圖像的特征提取,、模式識別中。
    近幾年來, 曲線擬合是計算機輔助幾何設計中的一個重要研究課題, 在計算機圖形學,、逆向工程,、數(shù)值計算等方面有著廣泛的應用。人們提出了許多各具特色的曲線擬合算法用于曲線描述,，李二濤等人提出了一種基于最小二乘的曲面擬合算法[7],采用該算法進行曲面擬合, 擬合的曲面精度高,但是當出現(xiàn)尖峰厚尾的分布時,，很難確定其密度函數(shù)。分段低次樣條插值雖然計算簡單,、穩(wěn)定性好,、收斂性有保證且易于實現(xiàn)，但只能保證各小段曲線在連接處的連續(xù)性,，不能保證整件曲線的光滑性,。利用三次樣條插值，既可保持分段低次插值多項式,，又可提高插值函數(shù)光滑性,。在三次樣條中，通過限定每個三次多項式的一階和二階導數(shù),，使其在斷點處相等,，能夠成功地逼近每對斷點間的曲線，較好地確定所有內(nèi)部三次多項式,，與原曲線具有極大的相似性[8-11],。
     本文采用變形雅可比(p=4,q=3)-傅里葉矩對多焦面圖像特征提取， 用三次樣條對特征空間軌跡進行擬合[12-16],。


    第3類邊界條件是周期性條件,，如果y＝f(x)是以b-a 為周期的函數(shù),，于是S(x) 在端點處滿足條件S′(x1＋0)＝S′(xn-0)，S"(xn＋0)＝S"(xn-0),。
2曲線擬合實驗研究
2.1算法實施步驟
    (1)將數(shù)據(jù)庫中15張不同焦面的鬧羊花圖像進行小波變換邊緣檢測,，得到邊緣圖像，并作為樣本圖像,，以便下一步特征提取,然后從樣本圖像中選取8張圖像作為訓練圖像;
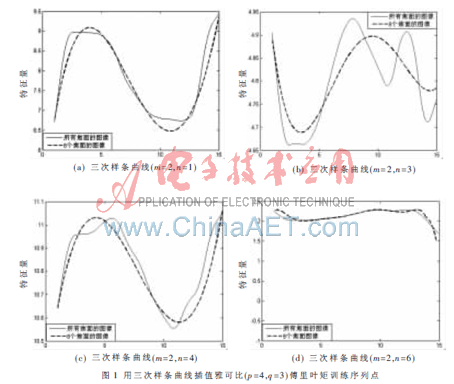
    (2)計算樣本圖像的變形雅可比(p=4,q=3)-傅里葉矩M=2,，N=0，1,，2,，…,N時的值，圖1所示為用三次樣條插值曲線插值變形雅可比(p=4,q=3)-傅里葉矩N=1,3,4,，6時的訓練序列點,。
    圖1中實線為數(shù)據(jù)庫中所有圖像的同一個變形雅可比(p=4,q=3)-傅里葉矩,虛線為訓練序列變形雅可比(p=4,q=3)-傅里葉矩M=2，N=1,3,4,6的三次樣條插值曲線,。

2.2 結(jié)果分析
     由圖1可知,，三次樣條插值曲線光滑地經(jīng)過訓練序列點，并且極其成功地擬合了變形雅可比(p=4,q=3)-傅里葉矩在M=2,，N=1,4,6的訓練序列點,。M=3時，三次樣條插值曲線對訓練序列點擬合得非常差,，說明該階矩所包含的圖像信息量非常少。在M=6時,兩條曲線最相似,，說明該階矩包含圖像的信息最多,。
    本文利用變形雅可比(p=4,q=3)-傅里葉矩描述多焦面圖像，該矩具有平移,、旋轉(zhuǎn),、灰度、尺度等多種畸變不變性和噪聲不敏感,，被廣泛用于圖像的特征提取,。采用三次樣條擬合特征空間軌跡,保證了插值函數(shù)光滑性，并且通過限定每個三次多項式的一階和二階導數(shù),，使其在斷點處相等,，成功地逼近每對斷點間的曲線。該方法可以有效地識別出含有圖像信息最豐富的矩值,。
參考文獻
[1] 阿木古楞, 楊性愉, 平子良. 基于變形雅可比(p=4,q=3)-傅里葉矩的形狀識別研究[J]. 模式識別與人工智能,2005,18(1):75-80.
[2] 平子良, 任海萍, 盛云龍,等.一種廣義正交不變圖像矩:雅可比-傅里葉矩[J].光電子·激光,2008,19(7):387-393.
[3] 王枚,王國宏,，高學強,等.基于小波變換和不變矩的車標識別方法[J].海軍航空工程學院學報,2007，23(6):655-658.
[4] FU B, ZHOU J Z, LI Y H, et al. Novel recursive and symmetric algorithm of fast computing two kinds of orthogonal radial moments, The Imaging Science Journal,2008,56:333-341.
[5] 陳月姣,阿木古楞,李凱智.計算變形雅可比-傅里葉矩的改進算法[J].光電子·激光,2010,21(6):940-943.
[6] 高國榮, 李文敏, 潘瓊.基于邊緣檢測與歸一化相關矩的圖像融合方法[J].計算機工程與應用,2008,44(27):194-196.
[7] 李二濤, 張國煊, 曾虹.基于最小二乘的曲面擬合算法研究[J].杭州電子科技大學學報,，2009,29(2):48-51.
[8] NEIBERG L, CASASENT D. Feature space trajectory classifier neural network.Proc.IEEE,1990,78(9):1481-1497.
[9] 孫同明,許珉, 楊育霞. 應用三次樣條函數(shù)快速計算插值FFT算法[J]. 電力自動化設備,2007,7(16):60-62.
[10] 夏省祥,于正文.三次樣條函數(shù)的自動求法[J]. 山東建筑工程學院學報,2003,18(4):86-89.
[11] Ping Ziliang,Sheng Yunlong,DESCHENES S, et al.Fourermellin descriptor and interpolated feature space trajectories  for three-dimensional object recognition[J].Society of Photo-Optical Instrumentation Engineers,2000,39(5):1260-1266.
[12] 姜志國,韓冬兵,薛斌黨,等.基于區(qū)域小波變換的序列顯微圖像融合[J]. 北京航空航大學學報,2006,，42(4):399-403.
[13] 徐麗群,葉子,徐善財,等.一種快速簡單多焦面顯微圖像融合方法[J].光學儀器, 2009,29(5):13-17.
[14] 邱元芳,，楊嗚.一種基于小波的顯微圖像融合算法[J].寧波大學學報,2006,19(3):286-289.
[15] 陳木生.圖像融合技術在圖像去噪中的應用[J].泉州師范學院學報,2007,25(2):49-51.
[16] 胡新榮,李德華,陳偉,等.從二維圖像序列獲取三維輪廓的算法及其實現(xiàn)[J]. 計算機工程與應用,2005,23:9-12.