隨著現(xiàn)代無線通信產(chǎn)業(yè)的快速發(fā)展，為了充分利用有限的無線頻譜資源,，現(xiàn)代通信系統(tǒng)采用了正交調(diào)制和多載波技術(shù),。然而這些技術(shù)對發(fā)射端前置高功率放大器(HPA)的線性度提出了非常高的要求[1]。在功率回退技術(shù),、負(fù)反饋法,、前饋線性化技術(shù)和數(shù)字預(yù)失真技術(shù)等常用的線性化技術(shù)中，數(shù)字基帶預(yù)失真技術(shù)因其成本低廉而得到了廣泛的應(yīng)用[2],。
    在基于查找表(LUT)數(shù)字基帶預(yù)失真(DPD)系統(tǒng)[3]的實現(xiàn)過程中,，DPD需要正確對比輸入信號x(n)和功率放大器輸出端的反饋信號z(n)。通常反饋信號相對于輸入信號有一段時間延遲,，這就破壞了預(yù)失真系統(tǒng)的穩(wěn)定性,，因此正確估計環(huán)路延遲并對其進(jìn)行補(bǔ)償就顯得十分必要。
    近年來,，國內(nèi)外學(xué)者對環(huán)路延遲估計進(jìn)行了分析并提出了一些估計算法,，如迭代法(Nagata Algorithm)[3]、延時鎖定環(huán)路法(DLL Method)[4]和相關(guān)檢測法(Correlation method)[5]等,，它們都有各自的優(yōu)缺點,。 本文結(jié)合參考文獻(xiàn)[6]提出的幅度差相關(guān)算法和參考文獻(xiàn)[7]中基于數(shù)據(jù)流相關(guān)運算的改進(jìn)算法提出了新的方法。該方法在用于FPGA實現(xiàn)時難度低于參考文獻(xiàn)[6],，同時在信號失真的情況下也能給出正確的估計值,。
1 環(huán)路延遲估計算法
    環(huán)路延遲是指信號從系統(tǒng)輸入端到反饋輸出端所產(chǎn)生的時間延遲。通常，反饋信號z(n)相對于輸入信號x(n)都會有一段時間的延遲,，并且該延遲會隨著時間和溫度的改變而改變,，故需要對其進(jìn)行實時估計。
    參考文獻(xiàn)[6]提出的幅度差相關(guān)法為：
  
    算法通過搜索R(m)的最大值得到環(huán)路延遲的估計值,。其通過對信號幅度的差取符號,，減少了運算量。但用于FPGA實現(xiàn)時,，需要復(fù)雜的時序控制，可實現(xiàn)度不高,。
    數(shù)據(jù)流相關(guān)運算的表達(dá)式為：
  
    此算法通過誤差的疊加盡量放大兩信號之間的差異。當(dāng)無整數(shù)倍延遲偏差時,，兩組數(shù)據(jù)差值最小,，故可以通過搜索R(m)的最小值得到整數(shù)倍環(huán)路延遲的估計值。由式(5)可知此算法具有運算復(fù)雜度低和易于實現(xiàn)的優(yōu)點,，但它要求反饋信號未經(jīng)衰落信道畸變及高斯噪聲影響才可以實現(xiàn),。
    針對上述兩種算法的不足，本文提出了新的方法,。其基本表達(dá)式為：
    
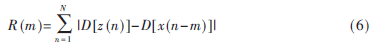
其中|·|表示取絕對值,，其他符號的定義與參考文獻(xiàn)[6]一致。
    由PA輸入,、輸出兩組數(shù)據(jù)具有一定的相關(guān)性可知,，當(dāng)沒有整數(shù)倍延遲偏差時，兩組數(shù)據(jù)差值最小,，故可以通過搜索R(m)的最小值得到整數(shù)倍環(huán)路延遲的估計值,。
    對比式(6)和式(1)可知，本方法在用于FPGA實現(xiàn)時比參考文獻(xiàn)[7]要減少一個計算D[x(n)]×D[z(n-m)]的步驟,；同時本方法在計算時只涉及到加減運算,，故其時序控制比參考文獻(xiàn)[6]簡單。對比式(6)和式(5),，本方法先通過式(2)保留信號的變化信息,，再通過式(6)保留輸入信號和反饋信號之間的相似性，故其不用像參考文獻(xiàn)[7]那樣對反饋信號有要求,。不過,，本方法和其他相關(guān)算法一樣要求輸入信號的周期必須大于環(huán)路延遲的值。
2 Matlab仿真結(jié)果及分析
    為了驗證本文所提方法的有效性,，進(jìn)行了仿真分析,。仿真所采用的系統(tǒng)框圖如圖1所示，其中PA行為模型采用的是并行維納結(jié)構(gòu)，OFDM信號延遲了22個周期,。

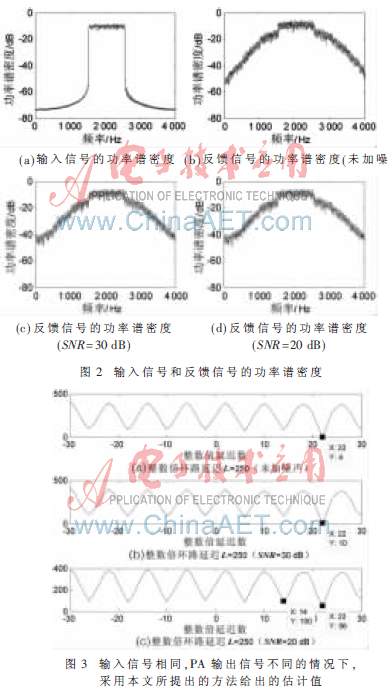
    為了驗證算法的魯棒性,，本文還給出了算法在反饋信號z(n)相對于輸入信號x(n)失真不同程度的情況下，環(huán)路延遲估計值,。其中,，輸入信號和反饋信號的功率譜密度如圖2所示。反饋信號是輸入信號經(jīng)過PA后未加噪聲,、而加了SNR=30 dB和SNR=20 dB的高斯白噪聲后得到的,。圖3所示為采用本文所提出的方法，對圖2中的信號進(jìn)行環(huán)路延遲估計給出的理論估計值,。由圖3可知,，當(dāng)反饋信號嚴(yán)重失真時，本文提出的方法也能給出正確的估計值,，從而證明了本文所提方法的有效性,。

3 環(huán)路延時估計的FPGA實現(xiàn)
    根據(jù)實際數(shù)字基帶預(yù)失真系統(tǒng)的需要，環(huán)路延時估計在采用FPGA芯片Stratix II EP2S60F672C4實現(xiàn)時,，“相關(guān)窗”的長度L取250,，共做了60次相關(guān)即k∈(0，60),，其實現(xiàn)的結(jié)構(gòu)框圖如圖4所示,。

    (1)接收存儲數(shù)據(jù)。將所要使用的數(shù)據(jù)存儲在FPGA的RAM中,，存儲的數(shù)據(jù)包含基帶發(fā)射信號及接收信號的實部,、虛部4組數(shù)據(jù)。

    (2)計算幅度差函數(shù)模塊,。由于使用信號幅度的平方代替幅度計算幅度差函數(shù)不改變幅度差函數(shù)D[·]的計算結(jié)果，同時FPGA中實現(xiàn)幅度的平方比幅度的復(fù)雜度更低,，故本模塊先根據(jù)式(7)計算出幅度的平方,，再根據(jù)式(2)的變形式(8)計算幅度差函數(shù)D[·]的值。
  
    (5)搜索最小項模塊,。本模塊采用的是數(shù)據(jù)比對存儲實現(xiàn)算法,，即當(dāng)輸入的數(shù)據(jù)與前一個輸入的數(shù)據(jù)相比較；存儲較小的數(shù)據(jù)及其自變量m的值,；60組數(shù)據(jù)比對完成后,，存儲在FPGA寄存器中的m值則是所要估計的整數(shù)倍環(huán)路延遲數(shù)目。
    (6)數(shù)據(jù)流控制模塊,。本模塊的目的是保證各個模塊能按既定的順序工作,。
4 系統(tǒng)調(diào)試
    為了驗證所設(shè)計模塊的正確性,，本文對比了輸入信號為八音信號且激發(fā)了PA的非線性的情況下，Matlab,、Modelsim和Signal Tap II中整數(shù)倍環(huán)路延遲估計模塊給出的估計值,。其中Matlab中信號的功率譜密度圖和延遲估計值如圖5所示。

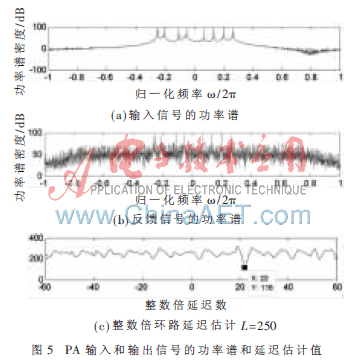
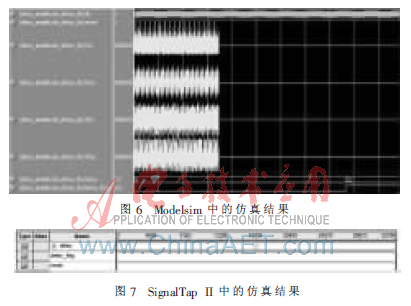
    將圖5中的信號導(dǎo)入Modelsim SE 6.5c進(jìn)行時序仿真,，仿真結(jié)果如圖6所示,。對比圖5、圖6可知,，本文所設(shè)計的實現(xiàn)方法是正確的,。
    最后把本文所設(shè)計的整數(shù)倍環(huán)路延遲估計模塊加入到數(shù)字基帶預(yù)失真系統(tǒng)中，進(jìn)行系統(tǒng)測試,。信號源所產(chǎn)生的信號功率譜如圖5所示，在SignalTap II中抓取的結(jié)果如圖7所示,，由圖可知，該模塊的功能是正確的,。

    本文針對數(shù)字基帶預(yù)失真系統(tǒng)中的延遲估計問題,，提出了一種易于FPGA實現(xiàn)的整數(shù)倍環(huán)路延遲估計的方法。由Matlab仿真結(jié)果可知,，本文所提出的方法在信號失真的情況下能正確給出環(huán)路延時的估計值,，從而證明了該方法的有效性。最后,，基于FPGA芯片Stratix II EP2S60F672C4設(shè)計實現(xiàn)了整數(shù)倍環(huán)路延遲估計模塊，由Modelsim SE 6.5c時序仿真和SignalTap II的硬件調(diào)試結(jié)果與Matlab理論仿真結(jié)果對比可知,，該實現(xiàn)方法是可行的,。本文設(shè)計的環(huán)路延遲估計模塊已經(jīng)應(yīng)用于數(shù)字基帶預(yù)失真系統(tǒng)。
參考文獻(xiàn)
[1] AI B,，YANG Z X,，PAN C Y，et al.Improved LUT technique  for HPA nonlinear pre-distortion in OFDM systems[J]. Wireless Personal Communications(S0929-6212),，2006,，38(4)：495-507.
[2] ANDING Z，DRAXLER P J,，YAN J J,，et al.Open-loop digital predistorter for RF power amplifiers using dynamic deviation reduction-based volterra series[J].Microwave Theory and Techniques[J]，IEEE Transactions on,，2008,，56(7)：1524-1534.
[3] NAGATA Y.Linear amplification technique for digital  mobile communications[C].In Vehicular Technology Conference,，IEEE 39th，1989.
[4] SHIGANG T,，KE G,，JUN W，et al.Loop delay correction  for adaptive digital linearization of power amplifiers[C].In Wireless Communications and Networking Conference,，WCNC 2007.
[5] RAWAT M,，et al.Adaptive digital predistortion for power  amplifiers with real time modeling of memoryless complex  gains[R].US Parent，2002.
[6] LI H,，KWON D H,，CHEN D，et al.A fast digital predistortion algorithm for radio-frequency power amplifier lineariza tion with loop delay compensation[J].IEEE Journal of Selected Topics in Signal Processing,，2009,，3(3)：374-383.
[7] 艾渤，鐘章隊,，朱剛,，等.放大器預(yù)失真系統(tǒng)中的環(huán)路延遲估計[J].系統(tǒng)仿真學(xué)報，2007,，19(19)：4487-4489.