神經(jīng)振蕩器是一種能夠在缺乏感官反饋或者高級控制命令的情況下，通過協(xié)調(diào)模式自發(fā)地產(chǎn)生規(guī)律輸出的神經(jīng)電路,。神經(jīng)振蕩器已經(jīng)被廣泛地應用于機器人的智能控制與生物研究中[1],，成為國內(nèi)外的研究熱點。相比于軟件編程,，神經(jīng)振蕩器的硬件實現(xiàn)具有高速,、并行處理、抗干擾等優(yōu)點,，更接近于其原有的生物特性,，因此引起了許多研究者的關注。在近些年來,，許多神經(jīng)振蕩器的硬件實現(xiàn)工作是基于模擬器件完成的[2-3],。雖然模擬電路能夠與生俱來地實現(xiàn)夠非線性函數(shù)，其功耗也相對較低,，但與可編程邏輯器件（FPGA）相比,，基于超大規(guī)模集成電路(VLSI)的工作需要相對長的設計周期，同時缺乏靈活性和兼容性,。另一方面,，F(xiàn)PGA已經(jīng)被廣泛地應用于人工神經(jīng)網(wǎng)絡(ANN)和智能控制電路硬件的實現(xiàn)[4-5]，但基于FPGA的神經(jīng)振蕩器實現(xiàn)國外才剛剛開始,，國內(nèi)尚未見報道,。且之前的工作大多基于乘法器的直接實現(xiàn)方法[6]，未能充分利用FPGA的資源,。
1 神經(jīng)振蕩器及其應用
    神經(jīng)振蕩器是一種耦合振蕩系統(tǒng),，通過神經(jīng)元之間的相互抑制實現(xiàn)穩(wěn)定的相位互鎖，并產(chǎn)生自激振蕩激發(fā)肢體做節(jié)律運動[7],。在仿生機器人控制中,，被控制對象往往存在非線性、系統(tǒng)工作點變化劇烈等特點,，傳統(tǒng)的控制往往是建立在單純依靠嚴格和精確數(shù)學模型基礎上,，但這種方法已難以滿足復雜多變且環(huán)境未知的機器人控制需求[8]。同時,，基于模型的機器人控制方法模型復雜,、解不唯一,、非結(jié)構(gòu)環(huán)境適應性較差等，不利于實現(xiàn)仿生機器人的快速穩(wěn)定運動[9],。神經(jīng)振蕩器具有非線性耦合的優(yōu)點,，很適合仿生機器人的節(jié)律運動控制，能達到快速穩(wěn)定的效果,。此外,，可以通過調(diào)整有限的神經(jīng)振蕩器參數(shù)，建立滿足具體要求不同的機器人與外界環(huán)境交互的復雜運動學,、動力學模型,，而不需要對整個系統(tǒng)建模，機器人的控制難度降低,?？傊?，基于神經(jīng)振蕩器控制的機器人具有以下優(yōu)點：（1）自動穩(wěn)定性,；（2）較強的環(huán)境適應性；（3）參數(shù)化建模[8-9],。
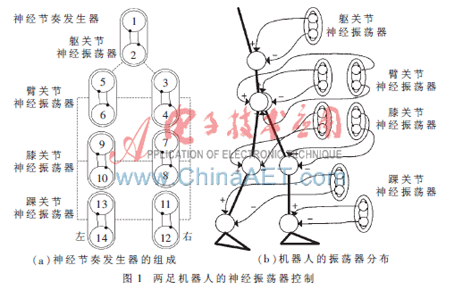
    圖1為神經(jīng)振蕩器應用于兩足機器人的一個例子,。該兩足機器人包含七個關節(jié)，其中包括一個軀關節(jié)（也可稱之為腰關節(jié)）,、兩個臀關節(jié),、兩個膝關節(jié)和兩個踝關節(jié)[10]。每一個神經(jīng)振蕩器由一對相互抑制的神經(jīng)元構(gòu)成,，每個關節(jié)由一個神經(jīng)振蕩器控制,。這樣，就可以將兩足機器人轉(zhuǎn)化為七個神經(jīng)振蕩器控制的神經(jīng)模式發(fā)生器系統(tǒng),，圖1（a）所示為模式發(fā)生器系統(tǒng)的組成,。通過調(diào)整振蕩器的參數(shù)，使各關節(jié)協(xié)調(diào)地做振蕩運動,，可以實現(xiàn)兩足機器人穩(wěn)定地行走等運動,。

2 分布式算法的改進
    傳統(tǒng)的分布式算法要求輸入為小數(shù)或整數(shù)。在FPGA系統(tǒng)中,，一般的輸入信號通過二進制小數(shù)點轉(zhuǎn)換模塊轉(zhuǎn)換為純小數(shù)(或者是整數(shù)),，輸出則剛好相反。本文對分布式算法做了修改,，使其不需要小數(shù)點轉(zhuǎn)移過程,。對于某一有符號的定點數(shù)xk，若其同時包含整數(shù)部分和小數(shù)部分,，xk可以用一個二進制數(shù)bN-1,，…,，b1，b0,，b-1,，…，b-M表示（共N+M=Q位,，N位整數(shù)位,，M位小數(shù)位）。bk,，N-1為符號位,，當bk，N-1=1時,，xk為負數(shù),，bk，N-1=0時,，xk為正數(shù),；bk，m為最低有效位,，代表xk能達到的最高精度,。
    
    同傳統(tǒng)的分布式方法一樣，這里的Lm事先輸入到查找表中,，通過加權累加器對查找表的輸出進行變更,、求和。對于K個輸入且輸出為y的分布式算法的原理如圖2所示[10],。

    分布式算法按時間周期進行運算,。一個時鐘周期是指變量xk的二進制編碼依次輸入到查找表（LUT）中累加求和所用的時間。一個時鐘周期包含M個時段,，每時段輸入二進制的一位,，第m=M-1位最先輸入，第m=0位最后輸入,。每輸入一位,，通過加權累加器求和。m=0的時間段稱為符號位時間,，其余時間段為非符號位時間,。一個時鐘周期包括符號位時間和非符號時間，當符號位時間到來并結(jié)束,，代表一個時間周期的結(jié)束和下一個時間周期的開始,，如圖2所示，符號時間結(jié)束,，開關從位置①打到位置②,，同時輸出y值,。
3 基于分布式算法的神經(jīng)振蕩器
    神經(jīng)振蕩器的設計可以在多個層次實現(xiàn)，如生物模型,、類神經(jīng)網(wǎng)絡模型和耦合振蕩器[1],。最廣泛使用的是神經(jīng)振蕩器，其實質(zhì)是交互抑制的非線性耦合振蕩器,。常見的耦合振蕩器模型有Amari-Hopfield,、Van De Pol和Matsuoka等，這些模型遵循相似的原理,。例如,，Amari-Hopfield振蕩器[2]的動力學方程如下式所示：
  
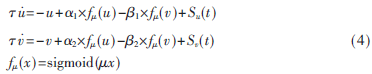
其中，u和v為神經(jīng)元的輸出,；Su(t)和Sv(t)為外部輸入,；α1、α2,、β1,、β2、μ為控制參數(shù),；fμ(x)為傳遞函數(shù),。如式(4)所示,，振蕩器的實現(xiàn)需要幾個基本操作：加減,、乘、積分求導和傳遞函數(shù)（可選）,。一個單獨的振蕩器只需要幾個乘法器,。然而，更大的振蕩器網(wǎng)絡需要更多抑制路徑與更多的乘法器來實現(xiàn),如果要實現(xiàn)一個7自由度的雙足機器人控制系統(tǒng),，將會需要上百的片上乘法器,，資源消耗十分巨大；另一方面,，大多數(shù)FPGA有大量的查找表（LUT）資源,。為了提高乘法效率，引入了分布式算法（DA）來優(yōu)化神經(jīng)振蕩器的FPGA實現(xiàn),，分布式算法利用了查找表而并非乘法器,。關于傳遞函數(shù)的FPGA實現(xiàn)問題，Tommiska已經(jīng)做了詳細的討論[11],。在這里使用飽和函數(shù)來取代雙級sigmoid函數(shù),。兩者的曲線圖十分相近，將式（4）中傳遞函數(shù)f?滋(x)用飽和函數(shù)代替,，替換后的振蕩模型的質(zhì)量沒有明顯降低,。
    
根據(jù)以上的方程,，可以方便地算出查找表的內(nèi)容，在這里不再贅述,。
4 分布式神經(jīng)振蕩器的FPGA硬件實現(xiàn)
    在Matlab/Simulink環(huán)境下,，使用Altera公司提供的DSP Builder工具箱[12]對基于分布式算法的神經(jīng)振蕩器進行建模，按照式（5）在Simulink中組建模塊,，得到的分布式神經(jīng)振蕩器的結(jié)構(gòu),。該系統(tǒng)主要包含了DA分布式算法、adder加法器,、integrator積分器,、transfer傳遞函數(shù)4個子模塊，系統(tǒng)采用20位定點數(shù)據(jù)的表述形式（整數(shù)部分為8位）,。
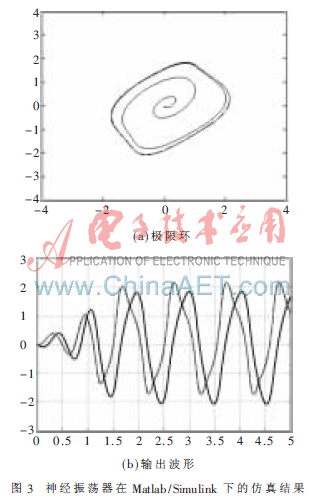
    Matlab/Simulink環(huán)境下仿真結(jié)果的極限環(huán)吸引子如圖3(a)所示,。其表明，對于從靜止狀態(tài)開始運動的神經(jīng)振蕩器,，經(jīng)過有限的時間,，最終會處于李雅普諾夫意義下的穩(wěn)定，即神經(jīng)振蕩器處于穩(wěn)定的振蕩過程而能量不衰減,。u和v的輸出波形如圖3(b)所示,。經(jīng)過約20 ?滋s的時間，神經(jīng)振蕩器進入穩(wěn)定的振蕩過程,。

    通過系統(tǒng)仿真,，該神經(jīng)振蕩器已達到設計要求，將模型文件.mdl轉(zhuǎn)化為硬件描述語言文件.vhd,，并對其綜合,。之后，在QuartusⅡ環(huán)境中打開由DSP Builder建立的QuartusⅡ工程文件,，就可以對生成的VHDL代碼進行器件配置,、引腳設定、硬件下載等工作,。當然,，該系統(tǒng)還可以作為制定硬件模塊被集成到NIOS II 軟核中，以方便對其調(diào)用與配置,。
5 實驗
    將程序下載到工作頻率為50 MHz的Altera Cyclone II EP2C8Q208芯片上,。通過Signal Tap II邏輯分析儀，獲得實驗數(shù)據(jù),，并將其導入Matlab中進行處理,、分析。計算可得,，u相輸出的實驗與仿真結(jié)果相關系數(shù)為0.99,，v也為0.99,，可見實驗結(jié)果和仿真結(jié)果高度一致，驗證了實驗的準確性,。
    據(jù)分析,，分布式算法節(jié)省了74%的查找表（LUT），75%的邏輯寄存器和100%的嵌入式乘法器,?？梢姡诜植际剿惴ǖ纳窠?jīng)振蕩器,，顯著地節(jié)約了硬件資源,。
    本文針對FPGA有限的算術乘法器提出了一個高效的神經(jīng)振蕩器實現(xiàn)方案。首先將分布式算法進行了改進,，使其可以直接處理同時帶有整數(shù)位和小數(shù)位的輸入信號,，并將改進的分布式算法應用到神經(jīng)振蕩器中。在Matlab/Simulink環(huán)境下,，通過DSP Builder建立了系統(tǒng)模型,。在保證了精確的實驗結(jié)果同時，與傳統(tǒng)的基于乘法器相比,，該方案顯著地節(jié)約了硬件資源,。此外，此方法還可以被應用到其他需要大量乘法運算的FPGA系統(tǒng)上,，如人工神經(jīng)網(wǎng)絡或者智能控制系統(tǒng),。
參考文獻
[1] IJSPEERT A J.Central pattern generators for locomotion  control in animals and robots：A review[J].Neural Net  works，May 2008(21)：642-653.
[2] NAKADA K,，ASAI T,，AMEMIYA Y.An analog CMOS central pattern generator for interlimb coordination in  quadruped locomotion[J].IEEE T Neural Networ,，2003(14)：1356-65.
[3] VOGELSTEIN R J,，TENORE F V G，GUEVREMONT L,，et al.A silicon central pattern generator controls locomotion in  Vivo[J].IEEE T Biomed Circ S.2008(2)：212-22.
[4] MISRA J,，SAHA I.Artificial neural networks in hardware：a survey of two decades of progress[J].Neurocomputing.2010(74)：239-55.
[5] MONMASSON E.FPGAs in industrial control applications[C]. Industrial Informatics，IEEE Transactions on.2011.
[6] TORRES H C,，GIRAU B.Implementation of central pattern generator in an FPGA-based embedded system[A].Artificial Neural Networks-ICANN.2010,，6353：276-285.
[7] 李彬.基于Wilson Cowan神經(jīng)振蕩器的四足機器人步態(tài)規(guī)劃研究[J].山東大學學報，2010,，1(40)：6-9.
[8] 李宏凱,，孫久榮，戴振東.動物運動指令的中樞模式發(fā)生器[J].機器人,，2008,，3(37)：279-288.
[9] GENTARO T.A  model  of  the  neuro-musculo-skeletal system  for  human  locomotion[J].Biological Cybernetics,，1995(73)：97-111.
[10] STANLEY A W.Applications of distributed arithmetic to digital signal processing：a tutorial review[J].IEEE ASSP Magazine，1989：4-15.
[11] TOMMISKA M T.Efficient digital implementation of the sigmoid function for reprogrammable logic[J].IEE P-Comput Dig T,，2003：403-411.
[12] 張志亮,，趙剛，齊星剛.從Simulink模型自動生成VHDL代碼—基于DSP Builder的FPGA設計流程[J].自動化技術,，2004(23)：4-6.